グラフィカル診断 Statsmodels

グラフィカル診断 Statsmodels

Statsmodelsは、Pythonの強力な統計モデリングツールです。

以下に、Statsmodelsのグラフィカル診断を紹介します。

グラフィカル診断

モデルの診断には様々なプロットを使用できます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import statsmodels.api as sm
import numpy as np

# サンプルデータの作成
data = sm.datasets.get_rdataset('mtcars').data

# モデルの作成
model = sm.OLS(data['mpg'], sm.add_constant(data[['hp', 'wt']])).fit()

# 残差プロット
sm.graphics.plot_regress_exog(model, 'hp')
sm.graphics.plot_regress_exog(model, 'wt')

# QQプロット
sm.qqplot(model.resid, line='s')

[実行結果]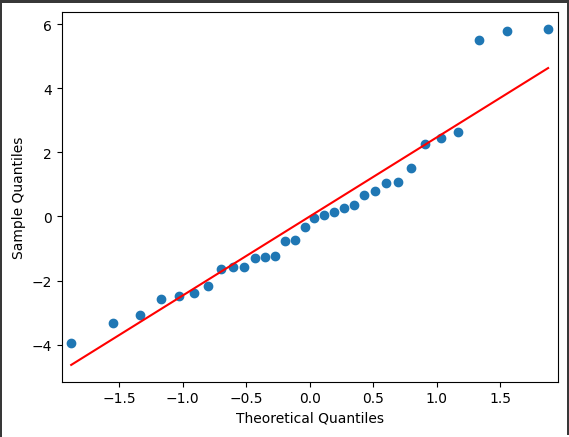


ソースコード解説

ソースコードの詳細な説明を行います。

1. 必要なライブラリのインポート

1
2
import statsmodels.api as sm
import numpy as np
  • statsmodels.api: 回帰分析や統計モデルのライブラリで、データ分析とモデル評価に広く使われます。
  • numpy: 数値計算のためのライブラリで、配列操作や数値演算を簡単に行えます。

2. サンプルデータの作成

1
data = sm.datasets.get_rdataset('mtcars').data
  • sm.datasets.get_rdataset('mtcars'): Rのデータセットを取得するメソッド。ここでは有名なmtcarsデータセットを使用しています。
  • data: mtcarsデータセットをデータフレームとして取得。

3. モデルの作成

1
model = sm.OLS(data['mpg'], sm.add_constant(data[['hp', 'wt']])).fit()
  • sm.OLS(endog, exog): OLS（最小二乗法）回帰モデルを作成するための関数。
    • endog: 被説明変数（目的変数）、ここでは燃費(mpg)。
    • exog: 説明変数（特徴量）、ここでは馬力(hp)と車両重量(wt)。
    • sm.add_constant(data[['hp', 'wt']]): 説明変数に定数項（切片）を追加。
  • fit(): モデルをデータに適合させるメソッド。

4. 残差プロット

1
2
sm.graphics.plot_regress_exog(model, 'hp')
sm.graphics.plot_regress_exog(model, 'wt')
  • sm.graphics.plot_regress_exog(model, exog_idx): 指定した説明変数に対する残差プロットを作成。
    • model: 作成した回帰モデル。
    • exog_idx: 残差プロットを作成する説明変数（ここではhpとwt）。

これにより、以下のような4つのグラフが生成されます。

  • Y and Fitted vs. X: 実測値と予測値のプロット。
  • Residuals versus X: 残差と説明変数のプロット。
  • Partial regression plot: 他の変数を固定した状態での説明変数と目的変数の関係を示すプロット。
  • CCPR Plot: 説明変数の影響を考慮した残差プロット。

5. QQプロット

1
sm.qqplot(model.resid, line='s')
  • sm.qqplot(data, line='s'): Q-Qプロットを作成するための関数。
    • data: プロットするデータ、ここでは回帰モデルの残差(model.resid)。
    • line='s': プロットに標準正規分布の参照線を追加。

まとめ

このコードは、mtcarsデータセットを用いて、燃費（mpg）を馬力（hp）と車両重量（wt）から予測する回帰モデルを作成し、モデルの評価を行っています。

具体的には、以下のことを行っています。

  1. mtcarsデータセットを取得。
  2. mpgを目的変数、hpとwtを説明変数とするOLS回帰モデルを作成し、適合。
  3. 説明変数に対する残差プロットを作成し、モデルの適合性を評価。
  4. 残差のQ-Qプロットを作成し、残差が正規分布に従っているかを確認。

これにより、モデルの性能や適合性、残差の特性を視覚的に評価することができます。

グラフ解説

表示されるグラフを解説します。

[実行結果1]

Q-Q プロット

  • 説明: Q-Qプロットは、データの分布が理論的な分布（通常は正規分布）にどれだけ近いかを視覚化するためのプロットです。
  • 見方: 点が赤い直線に近いほど、データが正規分布に従っていることを示しています。
  • 解釈: 多くの点が直線上にあるため、データは正規分布に近いと考えられます。ただし、端のほうでは少し外れている点もあり、これがデータの外れ値や分布の尾部の特性を示しています。

[実行結果2]

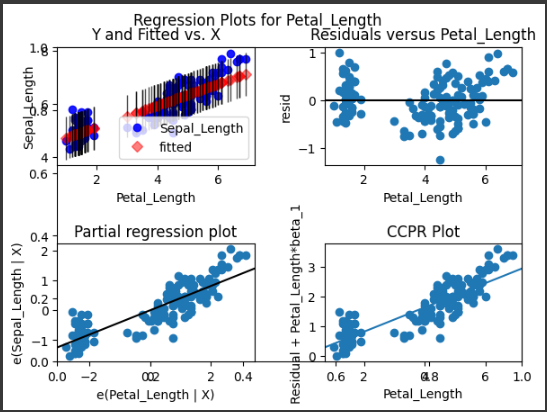
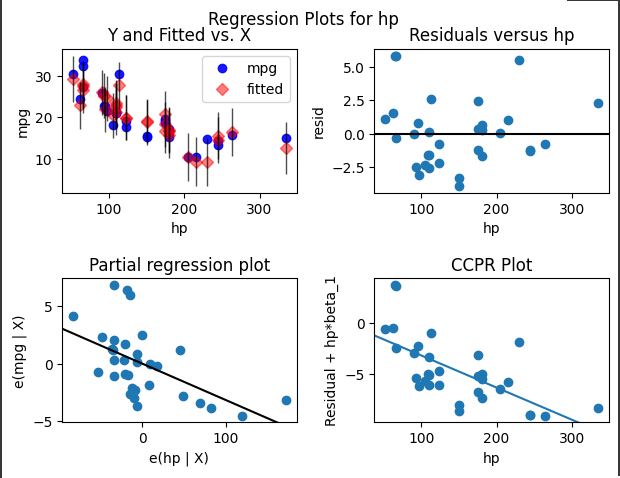
回帰プロット（hpに対する）

  • Y and Fitted vs. X: 実測値 (mpg) と予測値 (fitted) のプロット。予測値が実測値にどれだけ近いかを示しています。
  • Residuals versus hp: 残差（実測値と予測値の差）とhpのプロット。残差がランダムに散らばっている場合、モデルは適切です。
  • Partial regression plot: 他の変数を一定とした場合のhpとmpgの関係を示すプロット。
  • CCPR Plot: 残差プロットに相関を持たせたもの。各観測点の影響を視覚化しています。

解釈

  • Y and Fitted vs. X: 多くの点が一致しているため、モデルの予測は概ね正確です。
  • Residuals versus hp: 残差はランダムに分布しており、特定のパターンがないため、モデルは適切です。
  • Partial regression plot: hpが増加するにつれてmpgが減少していることを示しています。
  • CCPR Plot: hpの影響が残差に与える影響を示しており、負の関係が見られます。

[実行結果3]

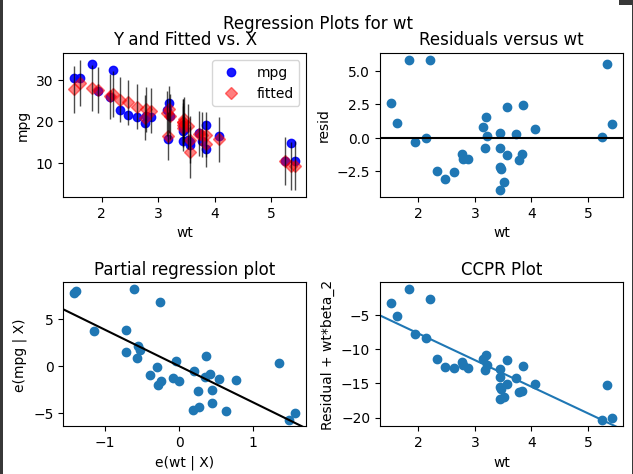
回帰プロット（wtに対する）

  • Y and Fitted vs. X: 実測値 (mpg) と予測値 (fitted) のプロット。予測値が実測値にどれだけ近いかを示しています。
  • Residuals versus wt: 残差とwtのプロット。残差がランダムに散らばっている場合、モデルは適切です。
  • Partial regression plot: 他の変数を一定とした場合のwtとmpgの関係を示すプロット。
  • CCPR Plot: 残差プロットに相関を持たせたもの。各観測点の影響を視覚化しています。

解釈

  • Y and Fitted vs. X: 実測値と予測値が近いため、モデルの予測は正確です。
  • Residuals versus wt: 残差がランダムに分布しており、特定のパターンがないため、モデルは適切です。
  • Partial regression plot: wtが増加するにつれてmpgが減少していることを示しています。
  • CCPR Plot: wtの影響が残差に与える影響を示しており、負の関係が見られます。

これらのプロットは、回帰モデルがどの程度データに適合しているか、残差がランダムに分布しているか、特定の変数の影響を視覚化するための有用なツールです。

python-constraint 学校の時間割

python-constraint 学校の時間割

以下の問題を解いてみましょう。

問題

学校の時間割

ある学校では、次の科目を月曜日から金曜日の$5$日間の授業時間に割り当てる必要があります。
各科目は$1$回ずつ行われ、各科目の授業は$1$日1時間だけです。

  • 数学（Math）
  • 英語（English）
  • 理科（Science）
  • 社会（SocialStudies）
  • 体育（PhysicalEducation）

条件：

  • 数学は月曜日か火曜日に行われる必要があります。
  • 英語は水曜日に行われる必要があります。
  • 体育は金曜日に行われる必要があります。

この条件に従って、時間割を作成してください。

解法

Python-Constraintライブラリを使って、条件に合った時間割を求めます。

コード

以下のコードを実行して、解を求めます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from constraint import Problem, AllDifferentConstraint

# 科目のリスト
subjects = ['Math', 'English', 'Science', 'SocialStudies', 'PhysicalEducation']

# 曜日のリスト
days = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']

# 問題を作成
problem = Problem()

# 各曜日に科目を割り当てる
for day in days:
    problem.addVariable(day, subjects)

# 各曜日には異なる科目が割り当てられるように制約を追加
problem.addConstraint(AllDifferentConstraint(), days)

# 数学は月曜日か火曜日に行われる必要がある
def math_on_monday_or_tuesday(monday, tuesday):
    return monday == 'Math' or tuesday == 'Math'

# 英語は水曜日に行われる必要がある
def english_on_wednesday(wednesday):
    return wednesday == 'English'

# 体育は金曜日に行われる必要がある
def pe_on_friday(friday):
    return friday == 'PhysicalEducation'

# 制約を追加
problem.addConstraint(math_on_monday_or_tuesday, ['Monday', 'Tuesday'])
problem.addConstraint(english_on_wednesday, ['Wednesday'])
problem.addConstraint(pe_on_friday, ['Friday'])

# 解を求める
solutions = problem.getSolutions()

# 結果を表示
if solutions:
    for solution in solutions:
        print(solution)
else:
    print("解が見つかりませんでした。")

このコードでは、指定された条件に従って$5$日間の学校の時間割を作成します。

結果として、各曜日にどの科目を割り当てるかが表示されます。

ソースコード解説

以下は、ソースコードの詳細な説明です。

1. 必要なライブラリのインポート

1
from constraint import Problem, AllDifferentConstraint
  • constraint ライブラリから Problem と AllDifferentConstraint をインポートしています。
    • Problem は制約充足問題を定義するためのクラスです。
    • AllDifferentConstraint はすべての変数に異なる値を割り当てる制約を定義するためのクラスです。

2. 科目と曜日のリスト定義

1
2
3
4
5
# 科目のリスト
subjects = ['Math', 'English', 'Science', 'SocialStudies', 'PhysicalEducation']

# 曜日のリスト
days = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']
  • subjects は授業科目のリストです。
  • days は曜日のリストです。

3. 問題の作成

1
2
# 問題を作成
problem = Problem()
  • Problem クラスのインスタンスを作成し、問題を定義します。

4. 変数の追加

1
2
3
# 各曜日に科目を割り当てる
for day in days:
    problem.addVariable(day, subjects)
  • 各曜日に対して、可能な科目を変数として追加します。
  • addVariable メソッドを使用して、各曜日（変数）が subjects のいずれかの科目（値）を取ることを指定します。

5. 制約の追加

1
2
# 各曜日には異なる科目が割り当てられるように制約を追加
problem.addConstraint(AllDifferentConstraint(), days)
  • AllDifferentConstraint を使用して、すべての曜日に異なる科目が割り当てられるように制約を追加します。

6. 特定の制約を定義

1
2
3
4
5
6
7
8
9
10
11
# 数学は月曜日か火曜日に行われる必要がある
def math_on_monday_or_tuesday(monday, tuesday):
    return monday == 'Math' or tuesday == 'Math'

# 英語は水曜日に行われる必要がある
def english_on_wednesday(wednesday):
    return wednesday == 'English'

# 体育は金曜日に行われる必要がある
def pe_on_friday(friday):
    return friday == 'PhysicalEducation'
  • 特定の制約条件を関数として定義します。
    • math_on_monday_or_tuesday は、数学が月曜日か火曜日に行われる制約です。
    • english_on_wednesday は、英語が水曜日に行われる制約です。
    • pe_on_friday は、体育が金曜日に行われる制約です。

7. 制約の追加

1
2
3
4
# 制約を追加
problem.addConstraint(math_on_monday_or_tuesday, ['Monday', 'Tuesday'])
problem.addConstraint(english_on_wednesday, ['Wednesday'])
problem.addConstraint(pe_on_friday, ['Friday'])
  • 定義した制約関数を問題に追加します。
    • math_on_monday_or_tuesday を月曜日と火曜日に対して追加します。
    • english_on_wednesday を水曜日に対して追加します。
    • pe_on_friday を金曜日に対して追加します。

8. 解の求解

1
2
# 解を求める
solutions = problem.getSolutions()
  • getSolutions メソッドを使用して、問題のすべての解を求めます。

9. 結果の表示

1
2
3
4
5
6
# 結果を表示
if solutions:
    for solution in solutions:
        print(solution)
else:
    print("解が見つかりませんでした。")
  • 解が見つかった場合、すべての解を表示します。
  • 解が見つからなかった場合、その旨を表示します。

まとめ

このコードは、制約充足問題を用いて学校の時間割を作成するものです。

与えられた制約（曜日ごとに異なる科目を割り当て、特定の曜日に特定の科目を割り当てる）を満たすすべての解を求め、表示します。

結果解説

[実行結果]

{'Monday': 'SocialStudies', 'Tuesday': 'Math', 'Friday': 'PhysicalEducation', 'Wednesday': 'English', 'Thursday': 'Science'}
{'Monday': 'Science', 'Tuesday': 'Math', 'Friday': 'PhysicalEducation', 'Wednesday': 'English', 'Thursday': 'SocialStudies'}
{'Monday': 'Math', 'Tuesday': 'SocialStudies', 'Friday': 'PhysicalEducation', 'Wednesday': 'English', 'Thursday': 'Science'}
{'Monday': 'Math', 'Tuesday': 'Science', 'Friday': 'PhysicalEducation', 'Wednesday': 'English', 'Thursday': 'SocialStudies'}

これは、学校の時間割問題に対する解がいくつか見つかったことを示しています。

各解は、月曜日から金曜日までの各曜日にどの科目が割り当てられているかを示しています。

各解は異なる時間割を示していますが、いずれも指定された制約を満たしています。

それぞれの解について説明します：

  1. 解1:

    • 月曜日: 社会（SocialStudies）
    • 火曜日: 数学（Math）
    • 水曜日: 英語（English）
    • 木曜日: 理科（Science）
    • 金曜日: 体育（PhysicalEducation）

  2. 解2:

    • 月曜日: 理科（Science）
    • 火曜日: 数学（Math）
    • 水曜日: 英語（English）
    • 木曜日: 社会（SocialStudies）
    • 金曜日: 体育（PhysicalEducation）

  3. 解3:

    • 月曜日: 数学（Math）
    • 火曜日: 社会（SocialStudies）
    • 水曜日: 英語（English）
    • 木曜日: 理科（Science）
    • 金曜日: 体育（PhysicalEducation）

  4. 解4:

    • 月曜日: 数学（Math）
    • 火曜日: 理科（Science）
    • 水曜日: 英語（English）
    • 木曜日: 社会（SocialStudies）
    • 金曜日: 体育（PhysicalEducation）

これらの解は、以下の制約をすべて満たしています：

  • 数学は月曜日か火曜日に行われる。
  • 英語は水曜日に行われる。
  • 体育は金曜日に行われる。

このように、制約を満たしつつ複数の異なる時間割が存在することがわかります。

python-constraint 魔法陣

python-constraint 魔法陣

魔法陣を解く問題を考えます。

魔法陣とは、整数の$ ( n \times n ) $の正方行列で、行・列および対角線の各要素の和がすべて同じになるものです。

魔法陣問題の解決

以下の例では、$3\times3$の魔法陣を解きます。

$3\times3$の魔法陣の各行、列、および対角線の和は$15$である必要があります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import constraint

# 魔法陣のサイズ
n = 3

# 魔法陣の各セルに変数を割り当てる
problem = constraint.Problem()

# 各セルは1から9の整数を持つ
problem.addVariables(range(n * n), range(1, n * n + 1))

# 各セルの値は一意である必要がある
problem.addConstraint(constraint.AllDifferentConstraint())

# 行、列、対角線の和がすべて等しくなる制約を追加
magic_sum = n * (n * n + 1) // 2

# 行の制約
for row in range(n):
    problem.addConstraint(
        lambda a, b, c: a + b + c == magic_sum,
        [row * n + i for i in range(n)]
    )

# 列の制約
for col in range(n):
    problem.addConstraint(
        lambda a, b, c: a + b + c == magic_sum,
        [col + n * i for i in range(n)]
    )

# 対角線の制約
problem.addConstraint(
    lambda a, b, c: a + b + c == magic_sum,
    [i * (n + 1) for i in range(n)]
)
problem.addConstraint(
    lambda a, b, c: a + b + c == magic_sum,
    [(i + 1) * (n - 1) for i in range(n)]
)

# 解を取得
solutions = problem.getSolutions()

# 結果を表示
for solution in solutions:
    for row in range(n):
        print([solution[row * n + col] for col in range(n)])
    print()

説明

  1. 問題定義:

    • 魔法陣のサイズ n = 3 を定義します。
    • 各セルに変数を割り当て、各変数は$1$から$9$までの値を取ることができます。

  2. 制約の追加:

    • constraint.AllDifferentConstraint() を使用して、各セルの値が一意であることを保証します。
    • 各行、列、および対角線の和が magic_sum になるように制約を追加します。

  3. 解の取得と表示:

    • problem.getSolutions() を使用してすべての解を取得し、各解を表示します。

このコードは$3\times3$の魔法陣を解くもので、すべての解を表示します。

他のサイズの魔法陣に対しても、同様の方法で解くことができます。

ただし、サイズが大きくなると計算時間が増加するため注意が必要です。

結果解説

[実行結果]

[6, 1, 8]
[7, 5, 3]
[2, 9, 4]

[6, 7, 2]
[1, 5, 9]
[8, 3, 4]

[8, 1, 6]
[3, 5, 7]
[4, 9, 2]

[8, 3, 4]
[1, 5, 9]
[6, 7, 2]

[4, 3, 8]
[9, 5, 1]
[2, 7, 6]

[4, 9, 2]
[3, 5, 7]
[8, 1, 6]

[2, 9, 4]
[7, 5, 3]
[6, 1, 8]

[2, 7, 6]
[9, 5, 1]
[4, 3, 8]

これは、$3\times3$の魔法陣のすべての可能な解を表示した結果です。

$3\times3$の魔法陣は、各行、各列、そして$2$つの対角線の数の合計がすべて$15$になるような配置です。

以下に各魔法陣の配置を解説します。

  1. 最初の魔法陣:

    1
    2
    3
    [6, 1, 8]
    [7, 5, 3]
    [2, 9, 4]
    • 各行の和: $6+1+8=15$, $7+5+3=15$, $2+9+4=15$
    • 各列の和: $6+7+2=15$, $1+5+9=15$, $8+3+4=15$
    • 対角線の和: $6+5+4=15$, $8+5+2=15$

  2. 二番目の魔法陣:

    1
    2
    3
    [6, 7, 2]
    [1, 5, 9]
    [8, 3, 4]
    • 各行の和: $6+7+2=15$, $1+5+9=15$, $8+3+4=15$
    • 各列の和: $6+1+8=15$, $7+5+3=15$, $2+9+4=15$
    • 対角線の和: $6+5+4=15$, $2+5+8=15$

  3. 三番目の魔法陣:

    1
    2
    3
    [8, 1, 6]
    [3, 5, 7]
    [4, 9, 2]
    • 各行の和: $8+1+6=15$, $3+5+7=15$, $4+9+2=15$
    • 各列の和: $8+3+4=15$, $1+5+9=15$, $6+7+2=15$
    • 対角線の和: $8+5+2=15$, $6+5+4=15$

これらの結果は、すべて$3\times3$の魔法陣であり、どの行、列、および対角線の和もすべて$15$になります。

このように、魔法陣の問題は数学的な整合性を満たすように数値を配置するパズルです。

python-constraintの使い方

python-constraint

python-constraint は、制約プログラミングのライブラリで、制約を満たす解を探索するために使用されます。

ここでは、python-constraint を使用した基本的な使い方を説明します。

基本的な使い方

インストール

まず、python-constraint をインストールします。

1
pip install python-constraint

例題

以下は、基本的な制約プログラムの例です。

この例では、変数 x と y を設定し、それらに特定の制約を課して解を探索します。

  1. 変数 x と y が $1$ から $10$ までの整数である。
  2. 変数 x と y の和が $15$ である。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from constraint import *

# 問題を作成
problem = Problem()

# 変数を追加
problem.addVariable("x", range(1, 11))
problem.addVariable("y", range(1, 11))

# 制約を追加（和が15になるように）
def constraint_sum(x, y):
    return x + y == 15

problem.addConstraint(constraint_sum, ["x", "y"])

# 解を取得
solutions = problem.getSolutions()

# 結果を表示
for solution in solutions:
    print(solution)

[実行結果]

{'x': 10, 'y': 5}
{'x': 9, 'y': 6}
{'x': 8, 'y': 7}
{'x': 7, 'y': 8}
{'x': 6, 'y': 9}
{'x': 5, 'y': 10}

このスクリプトは、x と y が $1$ から $10$ の範囲にあり、それらの和が $15$ であるすべての解を探します。

より複雑な例

次に、より複雑な例として、異なる色でグラフの頂点を塗り分ける問題を解きます。

この例では、4つの頂点$ (A, B, C, D) $があり、隣接する頂点は異なる色で塗る必要があります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from constraint import *

# 問題を作成
problem = Problem()

# 変数を追加（各頂点に色を割り当てる）
colors = ["red", "green", "blue"]
vertices = ["A", "B", "C", "D"]
for vertex in vertices:
    problem.addVariable(vertex, colors)

# 隣接する頂点の制約を追加（異なる色で塗る）
problem.addConstraint(AllDifferentConstraint(), ["A", "B"])
problem.addConstraint(AllDifferentConstraint(), ["A", "C"])
problem.addConstraint(AllDifferentConstraint(), ["B", "D"])
problem.addConstraint(AllDifferentConstraint(), ["C", "D"])

# 解を取得
solutions = problem.getSolutions()

# 結果を表示
for solution in solutions:
    print(solution)

[実行結果]

{'A': 'blue', 'B': 'green', 'C': 'green', 'D': 'blue'}
{'A': 'blue', 'B': 'green', 'C': 'green', 'D': 'red'}
{'A': 'blue', 'B': 'green', 'C': 'red', 'D': 'blue'}
{'A': 'blue', 'B': 'red', 'C': 'green', 'D': 'blue'}
{'A': 'blue', 'B': 'red', 'C': 'red', 'D': 'green'}
{'A': 'blue', 'B': 'red', 'C': 'red', 'D': 'blue'}
{'A': 'green', 'B': 'blue', 'C': 'blue', 'D': 'red'}
{'A': 'green', 'B': 'blue', 'C': 'blue', 'D': 'green'}
{'A': 'green', 'B': 'blue', 'C': 'red', 'D': 'green'}
{'A': 'green', 'B': 'red', 'C': 'blue', 'D': 'green'}
{'A': 'green', 'B': 'red', 'C': 'red', 'D': 'blue'}
{'A': 'green', 'B': 'red', 'C': 'red', 'D': 'green'}
{'A': 'red', 'B': 'green', 'C': 'green', 'D': 'red'}
{'A': 'red', 'B': 'green', 'C': 'green', 'D': 'blue'}
{'A': 'red', 'B': 'green', 'C': 'blue', 'D': 'red'}
{'A': 'red', 'B': 'blue', 'C': 'green', 'D': 'red'}
{'A': 'red', 'B': 'blue', 'C': 'blue', 'D': 'green'}
{'A': 'red', 'B': 'blue', 'C': 'blue', 'D': 'red'}

このスクリプトは、4つの頂点があり、それぞれが3つの色（赤、緑、青）のいずれかに塗られるようにし、隣接する頂点が異なる色で塗られるすべての解を探します。

その他の制約

python-constraint には他にもさまざまな制約を追加する方法があります。

例えば、以下のような制約があります。

  • AllDifferentConstraint(): すべての変数が異なる値を持つようにする。
  • ExactSumConstraint(total): 変数の和が特定の値に等しくなるようにする。
  • MaxSumConstraint(max_sum): 変数の和が特定の最大値を超えないようにする。

これらの制約を適用することで、より複雑な問題を解くことができます。

まとめ

python-constraint は、制約プログラミングを簡単に行うための強力なツールです。

変数と制約を定義し、getSolutions() メソッドを使用して解を探索します。

簡単な例から始めて、徐々に複雑な問題に取り組むことで、python-constraint の使い方に習熟できます。

statsmodels 住宅価格予測

statsmodels 住宅価格予測

statsmodelsを使用して現実的な問題を解決する方法を示します。

ここでは、重回帰分析を例に取り上げます。

例えば、住宅価格を予測するためのモデルを構築します。

データセットとして、よく知られているボストン住宅価格データセットを使用します。

このデータセットには、住宅の価格とそれに関連する様々な特徴量が含まれています。

以下の手順で進めます：

  1. データの読み込み
  2. データの前処理
  3. モデルの構築
  4. 結果の解釈

手順

1. データの読み込み

まず、必要なライブラリをインポートし、データセットを読み込みます。

1
2
3
4
5
import statsmodels.api as sm
import pandas as pd

# ボストン住宅価格データセットの読み込み
boston = sm.datasets.get_rdataset("Boston", "MASS").data

2. データの前処理

データを見て、ターゲット変数（住宅価格）と説明変数（特徴量）を分けます。

1
2
3
4
5
6
# データの確認
print(boston.head())

# 説明変数とターゲット変数の分割
X = boston.drop(columns=['medv'])  # 説明変数
y = boston['medv']  # ターゲット変数

3. モデルの構築

statsmodelsを使って重回帰モデルを構築します。

1
2
3
4
5
# 定数項を追加
X = sm.add_constant(X)

# モデルの構築
model = sm.OLS(y, X).fit()

4. 結果の解釈

モデルの結果を表示し、解釈します。

1
2
# 結果の表示
print(model.summary())

完全なコード

以下に完全なコードを示します：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import statsmodels.api as sm
import pandas as pd

# ボストン住宅価格データセットの読み込み
boston = sm.datasets.get_rdataset("Boston", "MASS").data

# データの確認
print(boston.head())

# 説明変数とターゲット変数の分割
X = boston.drop(columns=['medv'])  # 説明変数
y = boston['medv']  # ターゲット変数

# 定数項を追加
X = sm.add_constant(X)

# モデルの構築
model = sm.OLS(y, X).fit()

# 結果の表示
print(model.summary())

[実行結果]

      crim    zn  indus  chas    nox     rm   age     dis  rad  tax  ptratio  \
0  0.00632  18.0   2.31     0  0.538  6.575  65.2  4.0900    1  296     15.3   
1  0.02731   0.0   7.07     0  0.469  6.421  78.9  4.9671    2  242     17.8   
2  0.02729   0.0   7.07     0  0.469  7.185  61.1  4.9671    2  242     17.8   
3  0.03237   0.0   2.18     0  0.458  6.998  45.8  6.0622    3  222     18.7   
4  0.06905   0.0   2.18     0  0.458  7.147  54.2  6.0622    3  222     18.7   

    black  lstat  medv  
0  396.90   4.98  24.0  
1  396.90   9.14  21.6  
2  392.83   4.03  34.7  
3  394.63   2.94  33.4  
4  396.90   5.33  36.2  
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   medv   R-squared:                       0.741
Model:                            OLS   Adj. R-squared:                  0.734
Method:                 Least Squares   F-statistic:                     108.1
Date:                Mon, 08 Jul 2024   Prob (F-statistic):          6.72e-135
Time:                        03:02:00   Log-Likelihood:                -1498.8
No. Observations:                 506   AIC:                             3026.
Df Residuals:                     492   BIC:                             3085.
Df Model:                          13                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         36.4595      5.103      7.144      0.000      26.432      46.487
crim          -0.1080      0.033     -3.287      0.001      -0.173      -0.043
zn             0.0464      0.014      3.382      0.001       0.019       0.073
indus          0.0206      0.061      0.334      0.738      -0.100       0.141
chas           2.6867      0.862      3.118      0.002       0.994       4.380
nox          -17.7666      3.820     -4.651      0.000     -25.272     -10.262
rm             3.8099      0.418      9.116      0.000       2.989       4.631
age            0.0007      0.013      0.052      0.958      -0.025       0.027
dis           -1.4756      0.199     -7.398      0.000      -1.867      -1.084
rad            0.3060      0.066      4.613      0.000       0.176       0.436
tax           -0.0123      0.004     -3.280      0.001      -0.020      -0.005
ptratio       -0.9527      0.131     -7.283      0.000      -1.210      -0.696
black          0.0093      0.003      3.467      0.001       0.004       0.015
lstat         -0.5248      0.051    -10.347      0.000      -0.624      -0.425
==============================================================================
Omnibus:                      178.041   Durbin-Watson:                   1.078
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              783.126
Skew:                           1.521   Prob(JB):                    8.84e-171
Kurtosis:                       8.281   Cond. No.                     1.51e+04
==============================================================================

結果の解釈

結果には以下の情報が含まれます：

  • R-squared: モデルがデータのどれだけを説明しているかを示す指標。
    $1$に近いほどモデルの説明力が高い。
  • Coefficients(coef): 各説明変数の回帰係数。
    これにより各特徴量が住宅価格にどのような影響を与えるかがわかります。
  • P-values: 各説明変数の有意性を示す値。
    一般的に、p値が$0.05$未満の変数は統計的に有意とされます。

このようにして、statsmodelsを使用して現実的な問題を解決することができます。

この例では、住宅価格を予測するための重回帰モデルを構築し、その結果を解釈しました。

statsmodels

statsmodels

statsmodelsは、統計モデルの推定や統計検定、データの可視化などを行うためのPythonライブラリです。

以下に、statsmodelsの便利な使い方をいくつか紹介します。

1. 線形回帰モデル

statsmodelsを使用して線形回帰モデルを構築し、データの関係性を解析できます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import statsmodels.api as sm
import pandas as pd

# データの準備
df = pd.DataFrame({
    'X': [1, 2, 3, 4, 5],
    'Y': [1, 2, 1.3, 3.75, 2.25]
})

X = df['X']
Y = df['Y']

# 定数項の追加
X = sm.add_constant(X)

# 回帰モデルの構築とフィッティング
model = sm.OLS(Y, X).fit()

# モデルの概要
print(model.summary())

[実行結果]

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      Y   R-squared:                       0.393
Model:                            OLS   Adj. R-squared:                  0.191
Method:                 Least Squares   F-statistic:                     1.942
Date:                Sun, 07 Jul 2024   Prob (F-statistic):              0.258
Time:                        02:26:29   Log-Likelihood:                -5.6369
No. Observations:                   5   AIC:                             15.27
Df Residuals:                       3   BIC:                             14.49
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.7850      1.012      0.776      0.494      -2.434       4.004
X              0.4250      0.305      1.393      0.258      -0.546       1.396
==============================================================================
Omnibus:                          nan   Durbin-Watson:                   3.369
Prob(Omnibus):                    nan   Jarque-Bera (JB):                0.554
Skew:                           0.641   Prob(JB):                        0.758
Kurtosis:                       1.993   Cond. No.                         8.37
==============================================================================

2. ロジスティック回帰

カテゴリカルデータに対してロジスティック回帰を適用する例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import statsmodels.api as sm
import numpy as np

# データの準備
np.random.seed(42)
df = pd.DataFrame({
    'X1': np.random.rand(100),
    'X2': np.random.rand(100),
    'Y': np.random.randint(0, 2, 100)
})

X = df[['X1', 'X2']]
Y = df['Y']

# 定数項の追加
X = sm.add_constant(X)

# ロジスティック回帰モデルの構築とフィッティング
model = sm.Logit(Y, X).fit()

# モデルの概要
print(model.summary())

[実行結果]

Optimization terminated successfully.
         Current function value: 0.677050
         Iterations 4
                           Logit Regression Results                           
==============================================================================
Dep. Variable:                      Y   No. Observations:                  100
Model:                          Logit   Df Residuals:                       97
Method:                           MLE   Df Model:                            2
Date:                Sun, 07 Jul 2024   Pseudo R-squ.:                 0.01611
Time:                        02:27:12   Log-Likelihood:                -67.705
converged:                       True   LL-Null:                       -68.814
Covariance Type:            nonrobust   LLR p-value:                    0.3299
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.4792      0.524      0.915      0.360      -0.547       1.506
X1             0.4080      0.688      0.593      0.553      -0.939       1.756
X2            -0.9362      0.701     -1.336      0.181      -2.309       0.437

3. 時系列解析

statsmodelsを使用してARIMAモデルなどの時系列解析を行うことができます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import statsmodels.api as sm
import pandas as pd

# 時系列データの準備
data = sm.datasets.co2.load_pandas().data
data = data.fillna(data.bfill())

# ARIMAモデルのフィッティング
model = sm.tsa.ARIMA(data['co2'], order=(1, 1, 1))
result = model.fit()

# モデルの概要
print(result.summary())

# 予測
forecast = result.forecast(steps=10)
print(forecast)

[実行結果]

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                    co2   No. Observations:                 2284
Model:                 ARIMA(1, 1, 1)   Log Likelihood               -1536.855
Date:                Sun, 07 Jul 2024   AIC                           3079.710
Time:                        02:27:49   BIC                           3096.910
Sample:                    03-29-1958   HQIC                          3085.984
                         - 12-29-2001                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1          0.8959      0.022     40.360      0.000       0.852       0.939
ma.L1         -0.7587      0.034    -22.509      0.000      -0.825      -0.693
sigma2         0.2250      0.006     39.341      0.000       0.214       0.236
===================================================================================
Ljung-Box (L1) (Q):                  55.87   Jarque-Bera (JB):                74.67
Prob(Q):                              0.00   Prob(JB):                         0.00
Heteroskedasticity (H):               1.13   Skew:                            -0.14
Prob(H) (two-sided):                  0.10   Kurtosis:                         3.84
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
2002-01-05    371.652800
2002-01-12    371.789687
2002-01-19    371.912318
2002-01-26    372.022178
2002-02-02    372.120597
2002-02-09    372.208766
2002-02-16    372.287753
2002-02-23    372.358514
2002-03-02    372.421906
2002-03-09    372.478695
Freq: W-SAT, Name: predicted_mean, dtype: float64

4. ANOVA（分散分析）

複数グループ間の平均値の差異を検定するためにANOVAを使用します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import statsmodels.api as sm
from statsmodels.formula.api import ols

# データの準備
df = sm.datasets.get_rdataset("iris").data

# 列名の変更
df.columns = [col.replace('.', '_') for col in df.columns]
print(df.columns)  # 変更後の列名の確認

# モデルの構築
model = ols('Sepal_Length ~ C(Species)', data=df).fit()

# ANOVAテーブル
anova_table = sm.stats.anova_lm(model, typ=2)
print(anova_table)

[実行結果]

Index(['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width',
       'Species'],
      dtype='object')
               sum_sq     df           F        PR(>F)
C(Species)  63.212133    2.0  119.264502  1.669669e-31
Residual    38.956200  147.0         NaN           NaN

5. 残差プロット

モデルの適合度を視覚的に評価するために、残差プロットを作成できます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import statsmodels.api as sm
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt

# データの準備
df = sm.datasets.get_rdataset("iris").data
df.columns = [col.replace('.', '_') for col in df.columns]

# モデルの構築（Sepal_LengthとPetal_Lengthの線形回帰）
model = ols('Sepal_Length ~ Petal_Length', data=df).fit()

# 残差のプロット
fig, ax = plt.subplots()
sm.graphics.plot_regress_exog(model, 'Petal_Length', fig=fig)
plt.show()

[実行結果]

6. 様々な統計検定

t検定やカイ二乗検定など、様々な統計検定を行うことができます。

t検定

1
2
3
4
5
6
7
8
9
10
from scipy import stats
import statsmodels.api as sm

# データの準備
df = sm.datasets.get_rdataset("iris").data
df.columns = [col.replace('.', '_') for col in df.columns]

# 2つの独立した標本のt検定
t_stat, p_value = stats.ttest_ind(df['Sepal_Length'], df['Petal_Length'])
print(f'T-statistic: {t_stat}, P-value: {p_value}')

[実行結果]

T-statistic: 13.098353108960858, P-value: 2.857104069581941e-31

カイ二乗検定

1
2
3
4
5
6
7
8
9
10
11
12
import pandas as pd
from scipy.stats import chi2_contingency
import statsmodels.api as sm

# データの準備
df = sm.datasets.get_rdataset("iris").data
df.columns = [col.replace('.', '_') for col in df.columns]

# カイ二乗検定
table = pd.crosstab(df['Species'], df['Sepal_Length'] > df['Sepal_Length'].median())
chi2, p, dof, ex = chi2_contingency(table)
print(f'Chi2: {chi2}, P-value: {p}')

[実行結果]

Chi2: 78.64285714285712, P-value: 8.37376079899524e-18

これらの例は、statsmodelsの基本的な使用方法を示していますが、このライブラリは他にも多くの機能を提供しており、統計解析やモデリングの幅広いニーズに応えることができます。

仮想通貨の価格分析

仮想通貨の価格分析

仮想通貨の分析には、価格データの取得、トレンドの分析、テクニカル指標の計算などが含まれます。

以下に、Pythonを使って簡単な仮想通貨の価格分析を行う方法を示します。

ここでは、Bitcoin（BTC）の価格データを取得し、移動平均を計算してプロットする例を紹介します。

必要なライブラリのインストール

まず、以下のライブラリをインストールしてください。

1
pip install pandas yfinance matplotlib

データの取得と分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt

# データの取得
btc = yf.Ticker("BTC-USD")
data = btc.history(period="1y")  # 過去1年間のデータを取得

# 移動平均の計算
data['MA50'] = data['Close'].rolling(window=50).mean()  # 50日移動平均
data['MA200'] = data['Close'].rolling(window=200).mean()  # 200日移動平均

# データのプロット
plt.figure(figsize=(14, 7))
plt.plot(data['Close'], label='BTC-USD Close Price')
plt.plot(data['MA50'], label='50-Day Moving Average')
plt.plot(data['MA200'], label='200-Day Moving Average')
plt.title('Bitcoin Price and Moving Averages')
plt.xlabel('Date')
plt.ylabel('Price (USD)')
plt.legend()
plt.show()

解説

  1. データの取得: yfinanceライブラリを使って、Bitcoinの過去1年間の価格データを取得します。
  2. 移動平均の計算: pandasを使って、50日移動平均と200日移動平均を計算します。
  3. データのプロット: matplotlibを使って、価格データと移動平均をプロットします。

この例では、Bitcoinの過去1年間の終値と、その50日および200日の移動平均を表示しています。
移動平均を使うことで、価格の長期的なトレンドを視覚的に把握することができます。

他の分析方法としては、相対力指数（RSI）、移動平均収束拡散指標（MACD）などのテクニカル指標の計算や、ボラティリティの分析なども可能です。

さらに高度な分析には、機械学習モデルを使った価格予測や、統計的手法を用いた異常検知などがあります。

[実行結果]

ソースコード解説

このPythonスクリプトは、Bitcoinの価格データを取得し、50日および200日移動平均を計算してプロットするものです。

以下、コードの各部分を詳しく説明します。

1. ライブラリのインポート

1
2
3
import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt

この章では、必要なライブラリをインポートしています。

  • yfinance: Yahoo Financeから金融データを取得するためのライブラリ。
  • pandas: データの操作や分析を行うためのライブラリ。
  • matplotlib.pyplot: データの可視化を行うためのライブラリ。

2. データの取得

1
2
btc = yf.Ticker("BTC-USD")
data = btc.history(period="1y")  # 過去1年間のデータを取得

この章では、Bitcoinの価格データを取得しています。

  • yf.Ticker("BTC-USD"): yfinanceライブラリを使用して、Bitcoin（ティッカーシンボル: BTC-USD）のデータを取得するためのオブジェクトを作成します。
  • btc.history(period="1y"): 過去1年間のBitcoinの履歴データを取得します。このデータには、日次の価格（始値、高値、安値、終値）、取引量などが含まれます。

3. 移動平均の計算

1
2
data['MA50'] = data['Close'].rolling(window=50).mean()  # 50日移動平均
data['MA200'] = data['Close'].rolling(window=200).mean()  # 200日移動平均

この章では、50日移動平均と200日移動平均を計算しています。

  • data['Close']: データフレームから終値の列を選択します。
  • rolling(window=50): 終値の列に対して、50日間の移動ウィンドウを作成します。
  • mean(): 移動ウィンドウ内の値の平均を計算します。この操作により、50日間の移動平均が計算されます。
  • data['MA50']: 50日移動平均を新しい列としてデータフレームに追加します。
  • 同様に、window=200として200日移動平均も計算し、data['MA200']列に追加します。

4. データのプロット

1
2
3
4
5
6
7
8
9
plt.figure(figsize=(14, 7))
plt.plot(data['Close'], label='BTC-USD Close Price')
plt.plot(data['MA50'], label='50-Day Moving Average')
plt.plot(data['MA200'], label='200-Day Moving Average')
plt.title('Bitcoin Price and Moving Averages')
plt.xlabel('Date')
plt.ylabel('Price (USD)')
plt.legend()
plt.show()

この章では、取得したデータと計算した移動平均をプロットしています。

  • plt.figure(figsize=(14, 7)): グラフのサイズを設定します。幅14インチ、高さ7インチの図を作成します。
  • plt.plot(data['Close'], label='BTC-USD Close Price'): Bitcoinの終値をプロットし、ラベルを「BTC-USD Close Price」に設定します。
  • plt.plot(data['MA50'], label='50-Day Moving Average'): 50日移動平均をプロットし、ラベルを「50-Day Moving Average」に設定します。
  • plt.plot(data['MA200'], label='200-Day Moving Average'): 200日移動平均をプロットし、ラベルを「200-Day Moving Average」に設定します。
  • plt.title('Bitcoin Price and Moving Averages'): グラフのタイトルを設定します。
  • plt.xlabel('Date'): x軸のラベルを「Date」に設定します。
  • plt.ylabel('Price (USD)'): y軸のラベルを「Price (USD)」に設定します。
  • plt.legend(): 凡例を表示します。
  • plt.show(): グラフを表示します。

これにより、Bitcoinの価格推移とその50日および200日移動平均が可視化されます。

グラフ解説

[実行結果]

このグラフは、Bitcoin（BTC-USD）の価格推移と移動平均を表示しています。

以下は、このグラフの詳細な説明です。

グラフの概要

  • 期間: 過去1年間（2023年7月から2024年7月）
  • データ: Bitcoinの終値（青線）
  • 移動平均:
    • 50日移動平均（オレンジ線）
    • 200日移動平均（緑線）

詳細な説明

  1. 価格の変動（青線）:

    • 2023年7月から2023年11月まで: Bitcoinの価格は$30,000 $USD以下で、比較的低い水準で推移しています。
    • 2023年11月から2024年3月にかけて: 大きな上昇トレンドが見られ、価格は$70,000 $USDに達しています。この期間は急激な価格上昇を示しています。
    • 2024年3月以降: 価格は乱高下を繰り返しながらも、全体的に下降傾向にあります。

  2. 50日移動平均（オレンジ線）:

    • 短期的な価格のトレンドを示しています。価格が50日移動平均を上回っているときは上昇トレンド、下回っているときは下降トレンドと解釈されます。
    • 2023年末から2024年3月にかけて上昇し、その後は価格の変動に応じて上下していますが、全体的には価格の動きに遅れて追従しています。

  3. 200日移動平均（緑線）:

    • 長期的な価格のトレンドを示しています。50日移動平均よりも滑らかな曲線で、価格の大きなトレンドを捉えています。
    • 2023年11月から2024年7月にかけて一貫して上昇しており、価格の全体的な上昇トレンドを示しています。

結論

  • 価格動向: Bitcoinの価格は2023年7月から2023年11月まで低迷していましたが、その後急激に上昇し、2024年3月にはピークに達しました。その後は価格が乱高下し、下降傾向にあります。
  • 移動平均の交差: 50日移動平均が200日移動平均を上回るとゴールデンクロスと呼ばれ、強気市場のサインとされます。
    一方、50日移動平均が200日移動平均を下回るとデッドクロスと呼ばれ、弱気市場のサインとされます。
    グラフからは、直近でデッドクロスが発生していることが確認でき、今後の価格動向に注意が必要です。

この分析は、投資の判断材料として役立つかもしれませんが、他の要因や指標も考慮することをお勧めします。

CVXPY ポートフォリオ最適化

CVXPY ポートフォリオ最適化

次のようなポートフォリオ最適化問題を考えてみましょう。

ポートフォリオ最適化問題

あなたは、以下の3つの資産に投資するポートフォリオを構築しようとしています：

  1. Stock_A
  2. Stock_B
  3. Bond_C

それぞれの資産の予想リターンとリスク（分散）は次の通りです：

  • Stock_A: リターン = $12%$、リスク（分散） = $0.04$
  • Stock_B: リターン = $10%$、リスク（分散） = $0.03$
  • Bond_C: リターン = $6%$、リスク（分散） = $0.01$

また、各資産間の共分散は以下のようになっています：

Stock_A Stock_B Bond_C
Stock_A 0.04 0.01 0.00
Stock_B 0.01 0.03 0.01
Bond_C 0.00 0.01 0.01

あなたの目標は、全体のリスクを最小限に抑えつつ、ポートフォリオの期待リターンが少なくとも9%となるように投資割合を決定することです。

制約条件

  1. 各資産への投資割合の合計は$1$（100%）でなければならない。
  2. 各資産への投資割合は$0$以上でなければならない（空売りはしない）。
  3. ポートフォリオの期待リターンは少なくとも9%でなければならない。

目的

上記の制約条件を満たしながら、ポートフォリオのリスク（分散）を最小化する投資割合を求めなさい。

ソースコード

2次計画法（Quadratic Programming, QP）を用いて上記の問題を解きます。

以下は、cvxpyを用いたポートフォリオ最適化のコード例です：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import cvxpy as cp
import numpy as np

# 投資可能な資産のリスト
assets = ['Stock_A', 'Stock_B', 'Bond_C']

# 予想リターンとリスク（分散）
returns = np.array([0.12, 0.10, 0.06])
risks = np.array([0.04, 0.03, 0.01])
covariance = np.array([
    [0.04, 0.01, 0.00],
    [0.01, 0.03, 0.01],
    [0.00, 0.01, 0.01]
])

# 変数の定義
weights = cp.Variable(len(assets))

# リスク（分散）の計算
risk = cp.quad_form(weights, covariance)

# 制約条件の定義
constraints = [
    cp.sum(weights) == 1,
    weights >= 0,
    cp.sum(weights * returns) >= 0.09
]

# 目的関数の定義（リスクの最小化）
prob = cp.Problem(cp.Minimize(risk), constraints)

# 問題の解決
prob.solve()

# 結果の表示
print("Status:", prob.status)
print("Optimal Weights:", weights.value)
print("Total Risk (Variance):", risk.value)

このコードは、cvxpyを用いて2次計画法を解き、ポートフォリオの最適な投資割合とリスクを求めます。

ソースコード解説

このソースコードは、ポートフォリオ最適化問題を解くために、Pythonの数理最適化ライブラリであるcvxpyを使用しています。

ソースコードを詳しく説明します。

1. 必要なライブラリのインポート

1
2
import cvxpy as cp
import numpy as np

最初に、数理最適化を行うためのcvxpyライブラリと、数値計算を行うためのnumpyライブラリをインポートします。

2. 投資可能な資産のリスト

1
assets = ['Stock_A', 'Stock_B', 'Bond_C']

ここでは、投資対象となる資産のリストを定義しています。

今回は、3つの資産（Stock_A, Stock_B, Bond_C）に投資します。

3. 予想リターンとリスク（分散）の定義

1
2
3
4
5
6
7
returns = np.array([0.12, 0.10, 0.06])
risks = np.array([0.04, 0.03, 0.01])
covariance = np.array([
    [0.04, 0.01, 0.00],
    [0.01, 0.03, 0.01],
    [0.00, 0.01, 0.01]
])
  • returnsは各資産の予想リターンを表します。
  • risksは各資産のリスク（分散）を表します。
  • covarianceは各資産間の共分散行列を表します。
    共分散行列は、資産間のリスクの相関関係を示します。

4. 変数の定義

1
weights = cp.Variable(len(assets))

ここでは、各資産に対する投資割合を表す変数weightsを定義しています。
weightsは、3つの要素を持つベクトルです（各資産に対する投資割合を示すため）。

5. リスク（分散）の計算

1
risk = cp.quad_form(weights, covariance)

ここでは、ポートフォリオ全体のリスクを計算しています。
cp.quad_formは、二次形式を計算するための関数で、ポートフォリオのリスク（分散）を求めるのに使用されます。

6. 制約条件の定義

1
2
3
4
5
constraints = [
    cp.sum(weights) == 1,
    weights >= 0,
    cp.sum(weights * returns) >= 0.09
]

ここでは、最適化問題の制約条件を定義しています。

  • cp.sum(weights) == 1：各資産の投資割合の合計は$1$（100%）でなければなりません。
  • weights >= 0：各資産の投資割合は$0$以上でなければなりません（空売りはしない）。
  • cp.sum(weights * returns) >= 0.09：ポートフォリオの期待リターンは少なくとも9%でなければなりません。

7. 目的関数の定義（リスクの最小化）

1
prob = cp.Problem(cp.Minimize(risk), constraints)

ここでは、最適化問題を定義しています。
目的関数はポートフォリオのリスク（分散）を最小化することです。
また、制約条件もここで設定します。

8. 問題の解決

1
prob.solve()

この行では、定義された最適化問題を解決します。
prob.solve()は、最適化問題を解くための関数です。

9. 結果の表示

1
2
3
print("Status:", prob.status)
print("Optimal Weights:", weights.value)
print("Total Risk (Variance):", risk.value)

最後に、最適化結果を表示します。

  • prob.status：最適化問題の解決ステータス（成功かどうか）を表示します。
  • weights.value：各資産に対する最適な投資割合を表示します。
  • risk.value：最適な投資割合で得られるポートフォリオの総リスク（分散）を表示します。

全体の流れ

このコードは、ポートフォリオ最適化問題を定義し、投資割合を決定することで、リスクを最小化しながら目標リターンを達成するためのものです。

数理最適化ライブラリcvxpyを使用して、制約条件を満たしつつ、ポートフォリオのリスクを最小限に抑える最適な投資割合を計算します。

結果解説

[実行結果]

Status: optimal
Optimal Weights: [0.38461538 0.17307692 0.44230769]
Total Risk (Variance): 0.011634615384615387

上記の実行結果は、ポートフォリオ最適化問題を解いた際に得られた最適な解答を示しています。

以下にそれぞれの項目について説明します。

1. Status: optimal

この「optimal」というステータスは、最適化問題が解決されたことを示しています。

具体的には、全ての制約条件を満たしながら、リスク（分散）を最小限に抑える投資割合が見つかったことを意味します。

2. Optimal Weights: [0.38461538 0.17307692 0.44230769]

これは、各資産に対する最適な投資割合を示しています。
具体的には、以下の通りです：

  • Stock_A: 38.46%
  • Stock_B: 17.31%
  • Bond_C: 44.23%

これらの割合に基づいて投資することで、リスクを最小限に抑えつつ、目標リターン（少なくとも9%）を達成することができます。

3. Total Risk (Variance): 0.011634615384615387

これは、最適な投資割合で得られるポートフォリオの総リスク（分散）を示しています。
具体的には、$0.0116$という値になっています。
この値が小さいほど、ポートフォリオ全体のリスクが低いことを意味します。

結論

この最適化結果から、以下の点が確認できます：

  • 最適な投資割合は、Stock_Aに約$38.46%$、Stock_Bに約$17.31%$、Bond_Cに約$44.23%$です。
  • この投資割合により、ポートフォリオの期待リターンが$9%$以上となり、かつリスク（分散）が最小化されます。

したがって、この結果を基に投資を行うことで、目標リターンを達成しつつ、リスクを最小限に抑えたポートフォリオを構築することができます。

PuLP 時間割作成問題

PuLP 時間割作成問題

学校や大学の時間割を作成する際には、特定の科目が特定の時間に配置されるようにする必要があります。

ここでは、時間割作成問題をPuLPで解決する方法を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import pulp as pl

# 教師、科目、時間スロットのリスト
teachers = ['T1', 'T2']
subjects = ['Math', 'Science', 'English']
time_slots = ['Monday 9am', 'Monday 11am', 'Wednesday 9am']

# 教師が教えられる科目
teacher_subjects = {
    'T1': ['Math', 'Science'],
    'T2': ['Science', 'English']
}

# 問題の定義
prob = pl.LpProblem("Timetable_Problem", pl.LpMinimize)

# 変数の定義
vars = pl.LpVariable.dicts("Schedule", (teachers, subjects, time_slots), 0, 1, pl.LpBinary)

# 制約条件の定義
# 1. 各科目は1つの時間スロットに配置される
for s in subjects:
    prob += pl.lpSum([vars[t][s][ts] for t in teachers for ts in time_slots]) == 1

# 2. 各教師は1つの時間スロットで1つの科目のみ教える
for t in teachers:
    for ts in time_slots:
        prob += pl.lpSum([vars[t][s][ts] for s in subjects]) <= 1

# 3. 教師は教えられる科目のみ教える
for t in teachers:
    for s in subjects:
        if s not in teacher_subjects[t]:
            for ts in time_slots:
                prob += vars[t][s][ts] == 0

# 問題の解決
prob.solve()

# 結果の表示
print("Status:", pl.LpStatus[prob.status])
for t in teachers:
    for s in subjects:
        for ts in time_slots:
            if vars[t][s][ts].varValue == 1:
                print(f"{t} will teach {s} at {ts}")

ソースコード解説

このソースコードは、教師、科目、時間スロットに関する時間割問題を解決するためにPuLPを使用しています。

以下に、コードの各章を詳しく説明します。

1. インポートとデータの定義

1
2
3
4
5
6
7
8
9
10
11
12
import pulp as pl

# 教師、科目、時間スロットのリスト
teachers = ['T1', 'T2']
subjects = ['Math', 'Science', 'English']
time_slots = ['Monday 9am', 'Monday 11am', 'Wednesday 9am']

# 教師が教えられる科目
teacher_subjects = {
    'T1': ['Math', 'Science'],
    'T2': ['Science', 'English']
}

説明:

  • pulp ライブラリを pl としてインポートします。
  • 教師、科目、時間スロットのリストを定義します。
  • teacher_subjects 辞書を用いて、各教師が教えることができる科目を定義します。

2. 問題の定義

1
2
# 問題の定義
prob = pl.LpProblem("Timetable_Problem", pl.LpMinimize)

説明:

  • LpProblem クラスを使って、新しい最適化問題を定義します。
    この問題の目的は、時間割の問題を解決することです。

目的関数は LpMinimize で、最小化することを示していますが、実際の目的関数はこのコードでは特に定義されていません。

3. 変数の定義

1
2
# 変数の定義
vars = pl.LpVariable.dicts("Schedule", (teachers, subjects, time_slots), 0, 1, pl.LpBinary)

説明:

  • LpVariable.dicts を使って、3次元のバイナリ変数を定義します。

vars[t][s][ts] は、教師 t が科目 s を時間スロット ts に教えるかどうかを示すバイナリ変数です。

$0 $または$ 1 $の値を取ります。

4. 制約条件の定義

4.1 各科目は1つの時間スロットに配置される

1
2
3
# 1. 各科目は1つの時間スロットに配置される
for s in subjects:
    prob += pl.lpSum([vars[t][s][ts] for t in teachers for ts in time_slots]) == 1

説明:

  • 各科目 s は、全ての教師と時間スロットに対して、ちょうど1回だけ教えられることを保証する制約です。
    lpSum 関数を使って、全ての教師と時間スロットにわたる変数の合計が$1$になるようにします。

4.2 各教師は$1$つの時間スロットで$1$つの科目のみ教える

1
2
3
4
# 2. 各教師は1つの時間スロットで1つの科目のみ教える
for t in teachers:
    for ts in time_slots:
        prob += pl.lpSum([vars[t][s][ts] for s in subjects]) <= 1

説明:

  • 各教師 t は、特定の時間スロット ts で、最大1つの科目 s を教えることを保証する制約です。

lpSum 関数を使って、各時間スロットにおける変数の合計が$1$以下になるようにします。

4.3 教師は教えられる科目のみ教える

1
2
3
4
5
6
# 3. 教師は教えられる科目のみ教える
for t in teachers:
    for s in subjects:
        if s not in teacher_subjects[t]:
            for ts in time_slots:
                prob += vars[t][s][ts] == 0

説明:

  • 各教師 t は、自分が教えることができない科目 s を教えないことを保証する制約です。teacher_subjects 辞書を参照し、教師が教えられない科目に対する変数を$0$に設定します。

5. 問題の解決

1
2
# 問題の解決
prob.solve()

説明:

  • 定義された問題を解決します。

PuLP の solve メソッドを使って、最適な解を見つけます。

6. 結果の表示

1
2
3
4
5
6
7
# 結果の表示
print("Status:", pl.LpStatus[prob.status])
for t in teachers:
    for s in subjects:
        for ts in time_slots:
            if vars[t][s][ts].varValue == 1:
                print(f"{t} will teach {s} at {ts}")

説明:

  • 解のステータスを表示します。pl.LpStatus[prob.status] は解の状態を示します（例えば、最適解が見つかったかどうか）。
  • 各教師、科目、時間スロットの組み合わせに対して、変数の値が$1$の場合、その教師がその時間にその科目を教えることを示すメッセージを表示します。

まとめ

このコードは、PuLP を使用して時間割作成問題を解決するための例です。

教師、科目、時間スロットの組み合わせに対してバイナリ変数を定義し、制約条件を設定して、問題を解決します。

最終的に、最適な時間割を表示します。

結果解説

[実行結果]

Status: Optimal
T1 will teach Math at Monday 11am
T2 will teach Science at Wednesday 9am
T2 will teach English at Monday 11am

この結果は、PuLPを使って時間割作成問題を解決した際の出力です。

出力の内容を以下に説明します。

結果の解釈

  • Status: Optimal

    • このステータスは、最適解が見つかったことを示しています。
      つまり、与えられた制約条件の下で最良の時間割が作成されたことを意味します。

  • T1 will teach Math at Monday 11am

    • 教師T1が、月曜日の午前11時に数学を教えることが決定されたことを示しています。

  • T2 will teach Science at Wednesday 9am

    • 教師T2が、水曜日の午前9時に科学を教えることが決定されたことを示しています。

  • T2 will teach English at Monday 11am

    • 教師T2が、月曜日の午前11時に英語を教えることが決定されたことを示しています。

解の詳細

この結果は、以下のような制約条件と目標に基づいています。

  1. 各科目は1つの時間スロットに配置される

    • どの科目も$1$つの時間スロットに割り当てられています。

  2. 各教師は1つの時間スロットで1つの科目のみ教える

    • 各教師は$1$つの時間スロットで$1$つの科目しか教えていません。
      例えば、T1は月曜日11amにMathを教え、他の時間帯には何も教えていません。

  3. 教師は教えられる科目のみ教える

    • 各教師は指定された科目のみを教えています。
      T2はScienceとEnglishを教えており、T1はMathを教えています。

このスケジュールは、与えられた制約をすべて満たしつつ、可能な最適な配置となるように調整されています。

PuLPがこの問題を効率的に解決し、最適な時間割を提供していることが分かります。

NumPy

NumPy

NumPyは、Pythonで科学計算を行うための強力なライブラリです。

以下にNumPyの便利な使い方をいくつか紹介します。

1. 配列の作成

NumPyの基本は配列（ndarray）です。

以下の方法で配列を作成できます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np

# 配列の作成
a = np.array([1, 2, 3, 4, 5])
print(a)

# ゼロ配列
b = np.zeros((3, 3))
print(b)

# 1配列
c = np.ones((2, 2))
print(c)

# 連続した数値の配列
d = np.arange(10)
print(d)

# 等間隔の数値の配列
e = np.linspace(0, 1, 5)
print(e)

[実行結果]

[1 2 3 4 5]
[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]
[[1. 1.]
 [1. 1.]]
[0 1 2 3 4 5 6 7 8 9]
[0.   0.25 0.5  0.75 1.  ]

2. 配列の形状変更

配列の形状を変更する方法です。

1
2
3
4
5
6
7
8
# 1次元配列を2次元に変更
a = np.array([1, 2, 3, 4, 5, 6])
b = a.reshape((2, 3))
print(b)

# 転置
c = b.T
print(c)

[実行結果]

[[1 2 3]
 [4 5 6]]
[[1 4]
 [2 5]
 [3 6]]

3. 配列の演算

配列同士の演算や、ブロードキャストを用いた演算が簡単にできます。

1
2
3
4
5
6
7
8
9
10
11
12
13
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# 要素ごとの演算
c = a + b
print(c)

d = a * b
print(d)

# ブロードキャスト
e = a + 10
print(e)

[実行結果]

[5 7 9]
[ 4 10 18]
[11 12 13]

4. 統計関数

NumPyには多くの統計関数があります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
a = np.array([1, 2, 3, 4, 5])

# 平均
mean = np.mean(a)
print(mean)

# 中央値
median = np.median(a)
print(median)

# 標準偏差
std = np.std(a)
print(std)

# 和
sum_ = np.sum(a)
print(sum_)

[実行結果]

3.0
3.0
1.4142135623730951
15

5. インデックスとスライシング

NumPy配列のインデックスとスライシングは非常に柔軟です。

1
2
3
4
5
6
7
8
9
10
a = np.array([1, 2, 3, 4, 5])

# インデックス
print(a[0])
print(a[-1])

# スライシング
print(a[1:3])
print(a[:2])
print(a[::2])

[実行結果]

1
5
[2 3]
[1 2]
[1 3 5]

6. 条件を使ったフィルタリング

条件を使って配列の要素をフィルタリングできます。

1
2
3
4
5
6
7
8
9
10
a = np.array([1, 2, 3, 4, 5])

# 条件を使ったフィルタリング
b = a[a > 2]
print(b)

# ブールインデックス
c = np.array([True, False, True, False, True])
d = a[c]
print(d)

[実行結果]

[3 4 5]
[1 3 5]

7. 線形代数

NumPyには線形代数のための関数も豊富に用意されています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 行列の作成
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 行列積
C = np.dot(A, B)
print(C)

# 逆行列
D = np.linalg.inv(A)
print(D)

# 固有値と固有ベクトル
eigvals, eigvecs = np.linalg.eig(A)
print(eigvals)
print(eigvecs)

[実行結果]

[[19 22]
 [43 50]]
[[-2.   1. ]
 [ 1.5 -0.5]]
[-0.37228132  5.37228132]
[[-0.82456484 -0.41597356]
 [ 0.56576746 -0.90937671]]

これらはNumPyの基本的な使い方の一部に過ぎません。

NumPyは非常に強力で多機能なライブラリなので、公式ドキュメントやチュートリアルを参考にしながら、さらに深く学んでいくことをお勧めします。