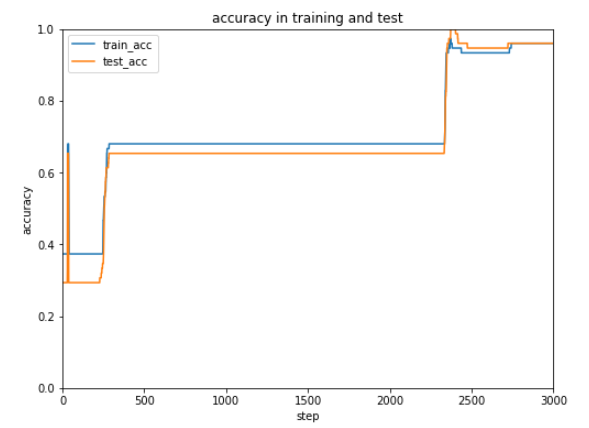
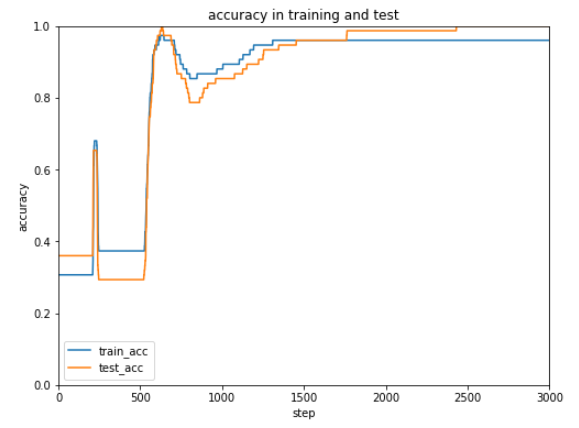
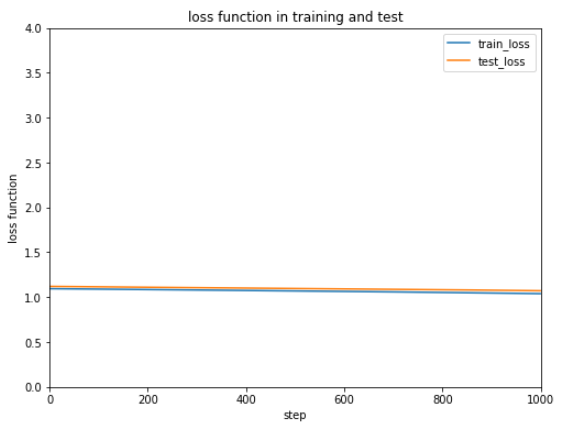
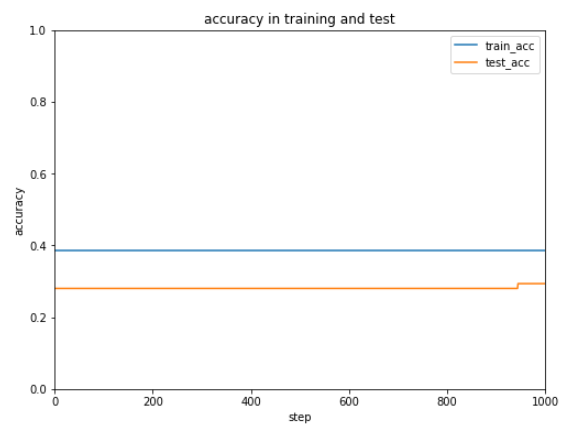
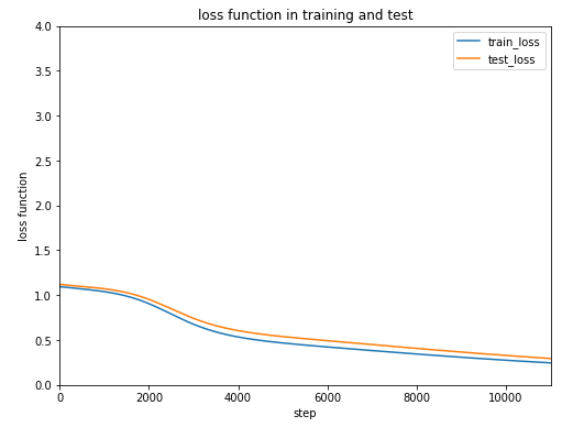
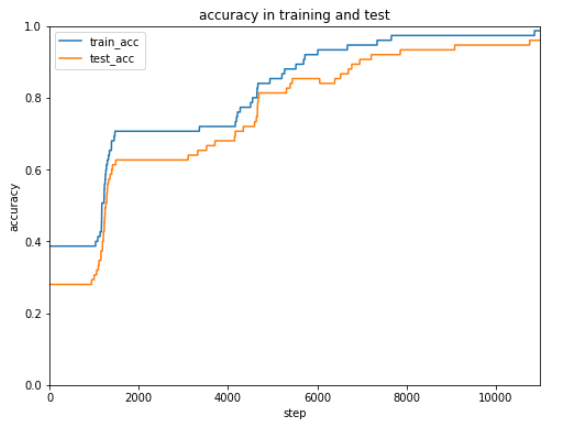
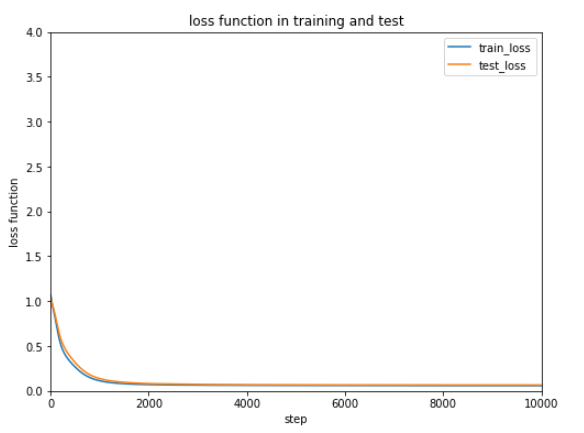
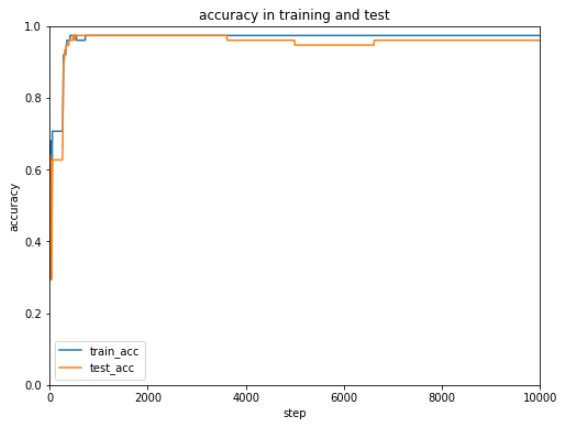
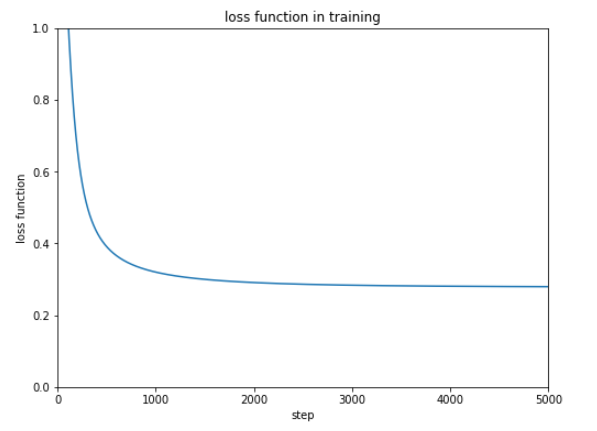
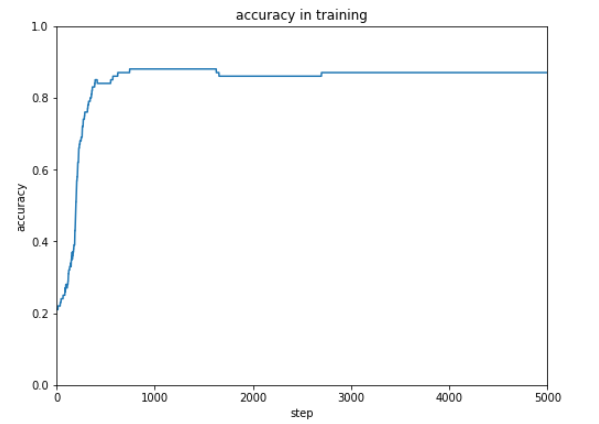
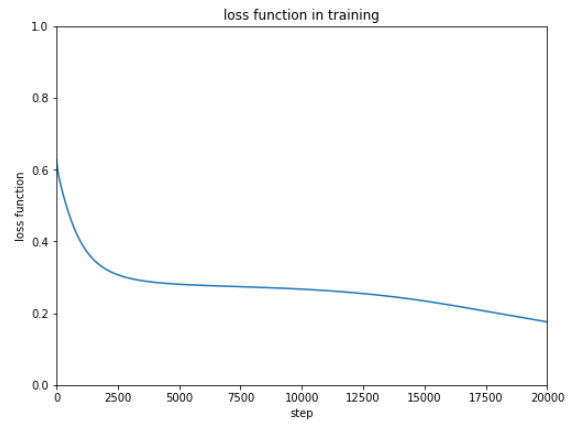
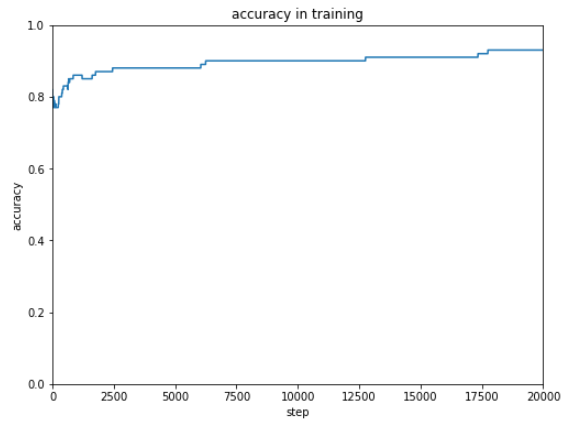
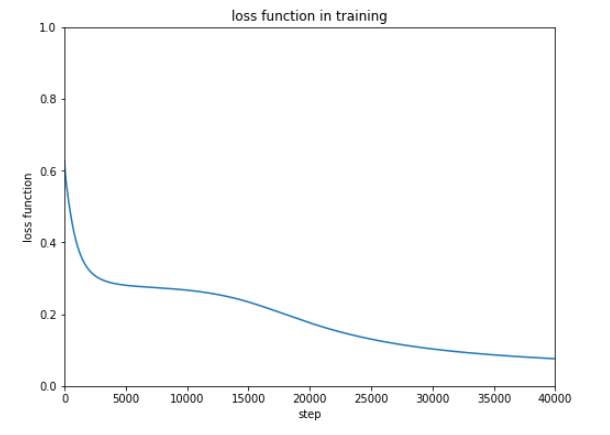
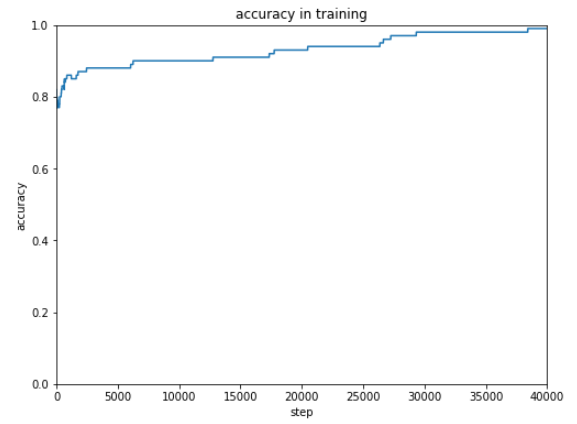
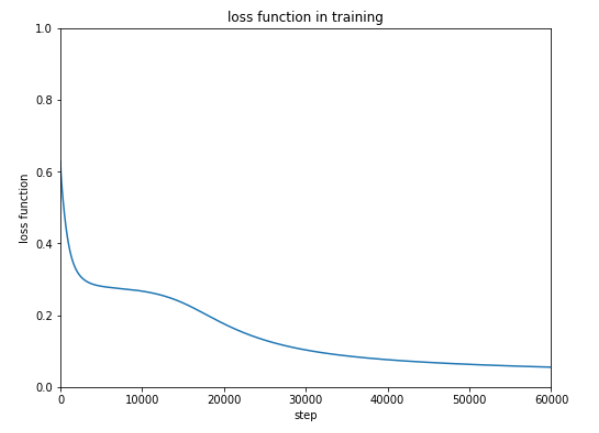
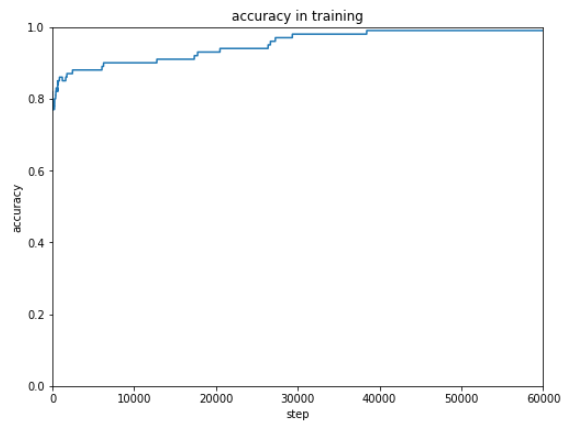
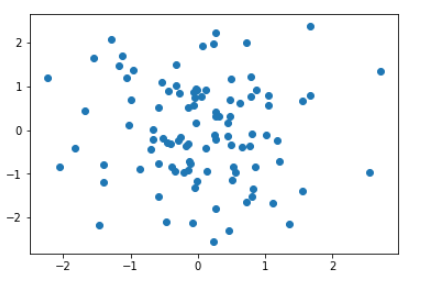
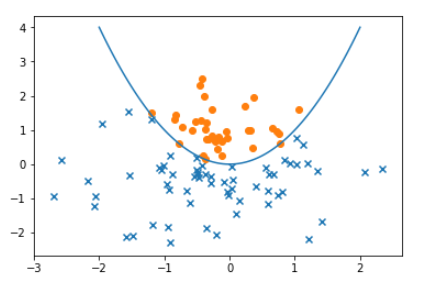
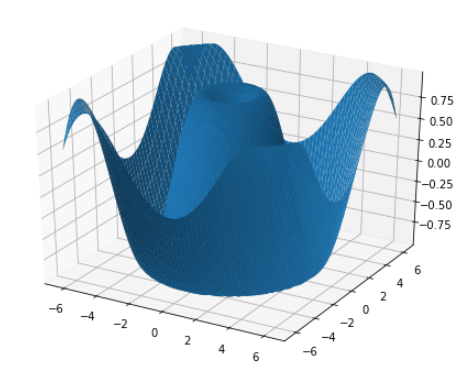
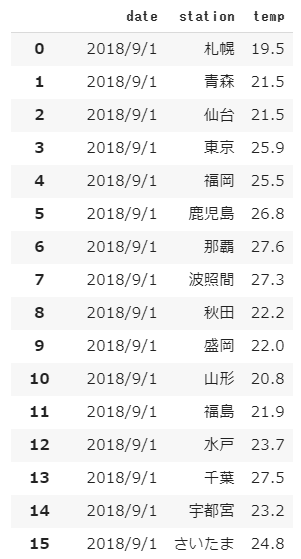
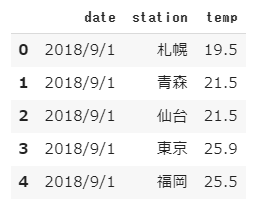
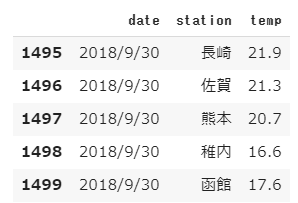
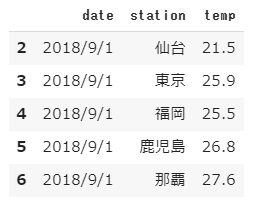
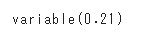前回使用したテストデータは10種ですが、次にもっと大きなデータを使ってテストするときのために正解率を表示できるようにしておきます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 score = [] for data in test_data: val = data.split(',' ) answer = int (val[0 ]) res = n_network.query((numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 ) res_max = numpy.argmax(res) print ('正解' , answer, '算出した答え' , res_max, '=>' , '〇' if answer == res_max else '×' ) score.append(1 if answer == res_max else 0 ) print ('# 正解率 # {:5.2f}%' .format (sum (score) / len (score) * 100 ))
【結果】
現状7割の正解率ですが学習データを増やしたり学習回数、学習率を調整してみます。
これまでは学習データ100個、テストデータ10個で簡単に動作確認してきましたが、今回は学習データ60,000個、テストデータ10,000個を使ってどのくらい正確に手書き文字を認識するかテストします。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 import numpyimport scipy.specialclass neural_network : def __init__ (self, in_node, hid_node, out_node, learn_rate ): self.in_node = in_node self.hid_node = hid_node self.out_node = out_node self.learn_rate = learn_rate self.weight_in_hid = numpy.random.normal(0.0 , pow (self.hid_node, -0.5 ), (self.hid_node, self.in_node)) self.weight_hid_out = numpy.random.normal(0.0 , pow (self.out_node, -0.5 ), (self.out_node, self.hid_node)) self.activation_func = lambda x: scipy.special.expit(x) def train (self, in_list, target_list ): in_matrix = numpy.array(in_list, ndmin=2 ).T target_matrix = numpy.array(target_list, ndmin=2 ).T hid_in = numpy.dot(self.weight_in_hid, in_matrix) hid_out = self.activation_func(hid_in) final_in = numpy.dot(self.weight_hid_out, hid_out) final_out = self.activation_func(final_in) out_err = target_matrix - final_out hid_err = numpy.dot(self.weight_hid_out.T, out_err) self.weight_hid_out += self.learn_rate * numpy.dot((out_err * final_out * (1.0 - final_out)), numpy.transpose(hid_out)) self.weight_in_hid += self.learn_rate * numpy.dot((hid_err * hid_out * (1.0 - hid_out)), numpy.transpose(in_matrix)) def query (self, input_list ): in_matrix = numpy.array(input_list, ndmin=2 ).T hid_in = numpy.dot(self.weight_in_hid, in_matrix) hid_out = self.activation_func(hid_in) final_in = numpy.dot(self.weight_hid_out, hid_out) final_out = self.activation_func(final_in) return final_out
次に今回使用する学習データ60,000個とテストデータ10,000個をダウンロードしておきます。
1 2 !wget https://www.pjreddie.com/media/files/mnist_train.csv !wget https://www.pjreddie.com/media/files/mnist_test.csv
60,000個の学習データを学習率0.2、学習回数(エポック)1回で学習させます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import numpyimport matplotlib.pyplot%matplotlib inline in_node = 784 hid_node = 200 out_node = 10 learn_rate = 0.2 n_network = neural_network(in_node, hid_node, out_node, learn_rate) with open ('mnist_train.csv' , 'r' ) as f: train_data = f.readlines() epochs = 1 for e in range (epochs): for record in train_data: val = record.split(',' ) in_data = (numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 target = numpy.zeros(out_node) + 0.01 target[int (val[0 ])] = 0.99 n_network.train(in_data, target)
10,000個のテストデータで正解率を算出します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 with open ('mnist_test.csv' , 'r' ) as f: test_data = f.readlines() score = [] for data in test_data: val = data.split(',' ) answer = int (val[0 ]) res = n_network.query((numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 ) res_max = numpy.argmax(res) score.append(1 if answer == res_max else 0 ) print ('# 正解率 # {:5.2f}%' .format (sum (score) / len (score) * 100 ))
【結果】
正解率をあげるため学習率や学習回数(エポック)を調整しようと考えていたのですが、もうすでに正解率95%以上と十分な正解率(認識率)となっています。
学習処理と検証処理を関数化します。引数に学習率を設定すると、その学習率での正解率が返ります。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 import numpydef train_test (learn_rate ): in_node = 784 hid_node = 200 out_node = 10 n_network = neural_network(in_node, hid_node, out_node, learn_rate) with open ('mnist_train.csv' , 'r' ) as f: train_data = f.readlines() epochs = 1 for e in range (epochs): for record in train_data: val = record.split(',' ) in_data = (numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 target = numpy.zeros(out_node) + 0.01 target[int (val[0 ])] = 0.99 n_network.train(in_data, target) with open ('mnist_test.csv' , 'r' ) as f: test_data = f.readlines() score = [] for data in test_data: val = data.split(',' ) answer = int (val[0 ]) res = n_network.query((numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 ) res_max = numpy.argmax(res) score.append(1 if answer == res_max else 0 ) return sum (score) / len (score) * 100
上記で定義した関数を学習率を変化させながら実行し、その結果を折れ線グラフに表示します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 %matplotlib inline import matplotlib.pyplot as pltx_data = [] y_data = [] for i in numpy.arange(0.1 , 1 , 0.1 ): x_data.append(i) y_data.append(train_test(i)) plt.xlabel("learn_rate" ) plt.ylabel("accuracy_rate(%)" ) plt.plot(x_data, y_data, marker='o' ) plt.show()
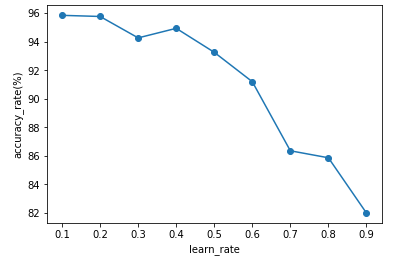
X軸に学習率、Y軸に正解率が表示されます。
上記の結果から学習率が0.1の場合が一番正解率が高いことがわかりました。
さきほど関数化したものの引数に学習回数を追加します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 import numpydef train_test (learn_rate, epochs ): in_node = 784 hid_node = 200 out_node = 10 n_network = neural_network(in_node, hid_node, out_node, learn_rate) with open ('mnist_train.csv' , 'r' ) as f: train_data = f.readlines() for e in range (epochs): for record in train_data: val = record.split(',' ) in_data = (numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 target = numpy.zeros(out_node) + 0.01 target[int (val[0 ])] = 0.99 n_network.train(in_data, target) with open ('mnist_test.csv' , 'r' ) as f: test_data = f.readlines() score = [] for data in test_data: val = data.split(',' ) answer = int (val[0 ]) res = n_network.query((numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 ) res_max = numpy.argmax(res) score.append(1 if answer == res_max else 0 ) return sum (score) / len (score) * 100
上記で定義した関数を学習回数を変化させながら実行し、その結果を折れ線グラフに表示します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 %matplotlib inline import matplotlib.pyplot as pltx_data = [] y_data = [] for i in numpy.arange(0.1 , 1 , 0.1 ): x_data.append(i) y_data.append(train_test(i)) plt.xlabel("learn_rate" ) plt.ylabel("accuracy_rate(%)" ) plt.plot(x_data, y_data, marker='o' ) plt.show()
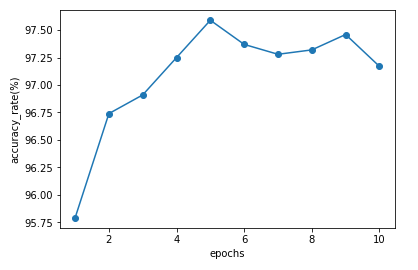
X軸に学習回数、Y軸に正解率が表示されます。
もともと学習回数が1回でも正解率95.75%となかなかの精度がでているのですが、学習回数をふやすとやや結果がよくなっていっているのがわかります。
関数化したものの引数に隠れ層の数を追加します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 import numpydef train_test (learn_rate, epochs, hid_node ): in_node = 784 out_node = 10 n_network = neural_network(in_node, hid_node, out_node, learn_rate) with open ('mnist_train.csv' , 'r' ) as f: train_data = f.readlines() for e in range (epochs): for record in train_data: val = record.split(',' ) in_data = (numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 target = numpy.zeros(out_node) + 0.01 target[int (val[0 ])] = 0.99 n_network.train(in_data, target) with open ('mnist_test.csv' , 'r' ) as f: test_data = f.readlines() score = [] for data in test_data: val = data.split(',' ) answer = int (val[0 ]) res = n_network.query((numpy.asfarray(val[1 :]) / 255.0 * 0.99 ) + 0.01 ) res_max = numpy.argmax(res) score.append(1 if answer == res_max else 0 ) return sum (score) / len (score) * 100
上記で定義した関数を隠れ層を変化させながら実行し、その結果を折れ線グラフに表示します。
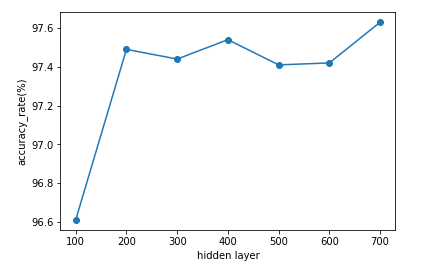
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 %matplotlib inline import matplotlib.pyplot as pltx_data = [] y_data = [] for i in range (100 , 701 , 100 ): x_data.append(i) y_data.append(train_test(0.1 , 5 , i)) plt.xlabel("hidden layer" ) plt.ylabel("accuracy_rate(%)" ) plt.plot(x_data, y_data, marker='o' ) plt.show()
X軸に隠れ層の数、Y軸に正解率が表示されます。
(Google Colaboratory で動作確認しています。)