A Versatile Visualization for Multi-Variable Analysis/span>
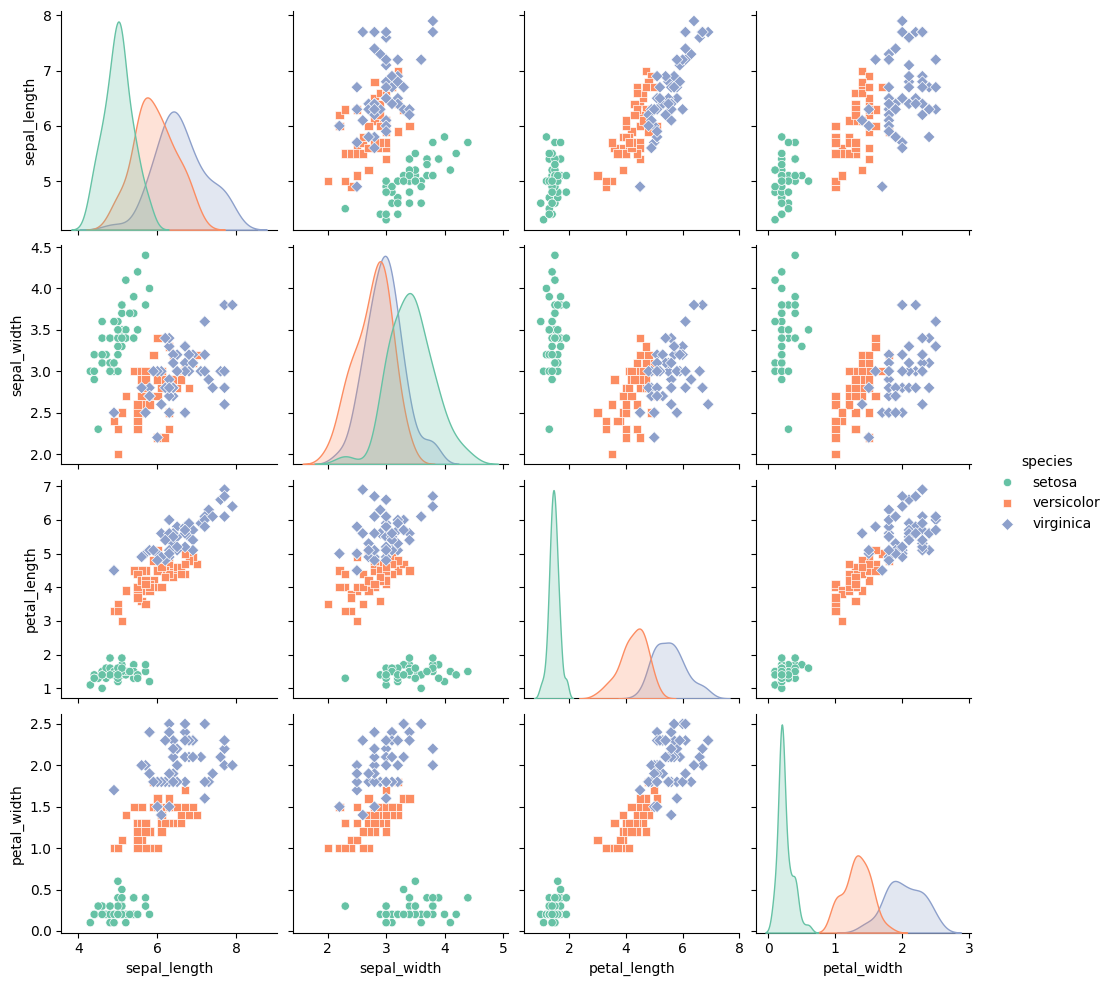
PairGrid in $Seaborn$ is a powerful tool for visualizing relationships across multiple variables in a single, customizable grid.
By using different plots on the diagonal and off-diagonal sections, we can present complex data in a format that highlights distribution and correlation simultaneously.
This method is particularly useful for exploratory data analysis, allowing us to examine each pair of variables with tailored visualizations that make it easier to identify patterns, outliers, and correlations.
In this example, we’ll use the iris dataset, which contains measurements for petal and sepal length and width for different iris flower species.
We’ll create a grid where the diagonal shows each variable’s distribution, while the off-diagonal displays scatter plots to visualize relationships between variable pairs.
Step-by-Step Explanation and Code
Load the Data:
Theirisdataset has four numerical features (sepal_length,sepal_width,petal_length,petal_width) and a categoricalspeciesfeature.Set Up the PairGrid:
We’ll create a grid where:- The diagonal displays histograms to show distributions of each variable.
- The off-diagonal cells show scatter plots, comparing each pair of variables and adding color to distinguish the species.
Customize the Plot:
We’ll add color palettes, improve the legend, and customize titles for better readability.
Here’s the full implementation:
1 | import seaborn as sns |
Detailed Explanation
Data Preparation:
- We load the
irisdataset, which includes four continuous features (sepal_length,sepal_width,petal_length, andpetal_width) and one categorical feature,species, which represents three types of iris flowers: setosa, versicolor, and virginica.
- We load the
PairGrid Setup:
sns.PairGrid(df, hue="species", palette="Set2"): Sets up aPairGridusing theirisdataset.
We specifyspeciesas thehueto color-code each species in the plot, and we use theSet2color palette for aesthetic differentiation.
Plot Mapping:
- Diagonal Plot (
map_diag):sns.histplotwithkde=Truedisplays histograms with kernel density estimation (KDE) on the diagonal, showing each variable’s distribution.
The KDE line smooths out the histogram, giving a clear view of each variable’s distribution. - Off-Diagonal Plot (
map_offdiag):sns.scatterplotdisplays scatter plots on the off-diagonal cells, showing pairwise relationships.
Withs=30andalpha=0.7, we adjust the marker size and transparency to avoid overlap and make the scatter plots clearer.
- Diagonal Plot (
Adding Customizations:
g.add_legend(title="Species"): Adds a legend to distinguish between species.g.fig.suptitle(...): Sets a title for the entire grid, positioned slightly above the grid withy=1.02for clarity.
Interpretation
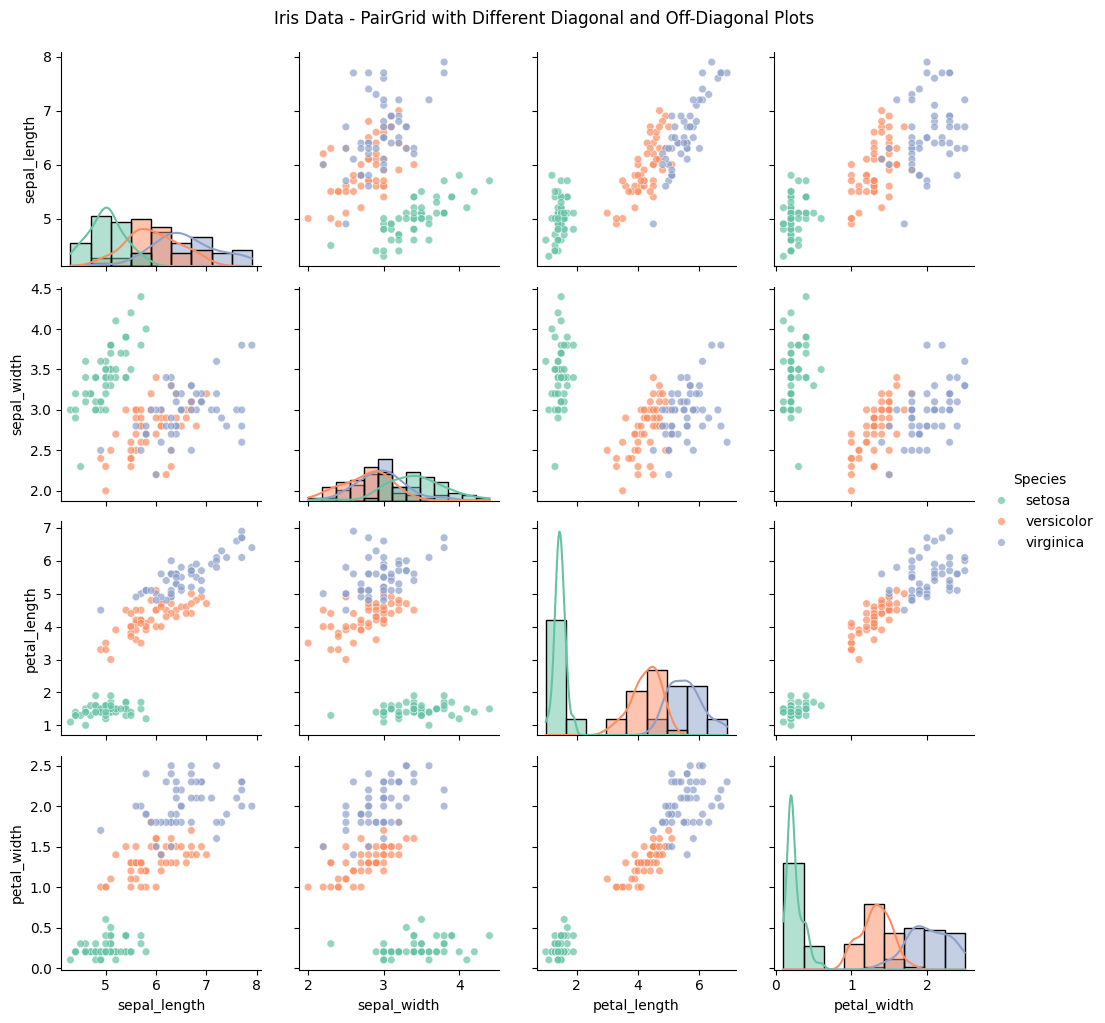
The resulting grid provides insights into both individual distributions and pairwise relationships:
- Diagonals (Distributions): Each diagonal cell shows the distribution of a single variable, allowing us to assess each species’ range and typical values for petal and sepal measurements.
- Off-Diagonals (Pairwise Relationships): The scatter plots in the off-diagonal cells show relationships between variable pairs. For example:
- A strong linear relationship between
petal_lengthandpetal_widthis observed, especially for the virginica species. - Overlaps or separations between species in scatter plots reveal which pairs of variables can differentiate species, aiding classification.
- A strong linear relationship between
Output
The output grid will have:
- Histograms along the diagonal, showing each variable’s distribution by species.
- Scatter plots in the off-diagonal, showing pairwise relationships between features, with color-coding for each species.
Conclusion
The PairGrid with different diagonal and off-diagonal plots in $Seaborn$ allows for a multi-faceted analysis of relationships and distributions within a dataset.
By customizing the plots, we can leverage both distributional and relational insights, making it a valuable visualization tool in data science for complex, multi-variable datasets.