Let’s explore cryptography problem: Modular Exponentiation.

This operation is fundamental in many cryptographic algorithms, especially public-key cryptography methods like $RSA$ encryption.

Modular exponentiation efficiently computes large powers of a number under a modulus, which is essential for encryption and decryption processes.

Problem: Modular Exponentiation

Given three integers $( a )$, $( b )$, and $( n )$, calculate $( a^b \mod n )$.

For large $( b )$, directly computing $( a^b )$ and then taking the modulus $( n )$ would be computationally intensive.

Instead, we can use an efficient algorithm called Exponentiation by Squaring to handle large powers.

Example

Let’s calculate $( 3^{45} \mod 13 )$:

• $( a = 3 )$
• $( b = 45 )$
• $( n = 13 )$

The solution involves repeatedly squaring and taking the modulus to avoid computing the large number $( 3^{45} )$ directly.

Objective

Use $Python$ to implement modular exponentiation and calculate $( a^b \mod n )$ efficiently.

Then, visualize the results of $( a^b \mod n )$ for various values of $( b )$ to see how the result changes as $( b )$ increases.

Python Code

Here’s the $Python$ code to solve the modular exponentiation problem and visualize the results:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import matplotlib.pyplot as plt

# Modular exponentiation function using Exponentiation by Squaring
def modular_exponentiation(a, b, n):
    result = 1
    base = a % n
    while b > 0:
        if b % 2 == 1:  # If b is odd, multiply the result by the base
            result = (result * base) % n
        b = b // 2
        base = (base * base) % n  # Square the base
    return result

# Parameters
a = 3  # Base
n = 13  # Modulus

# Calculate modular exponentiation for different powers of b
b_values = list(range(1, 46))  # Powers from 1 to 45
mod_exp_results = [modular_exponentiation(a, b, n) for b in b_values]

# Plot the results
plt.figure(figsize=(10, 6))
plt.plot(b_values, mod_exp_results, marker='o', linestyle='-', color='teal')
plt.xlabel('Exponent (b)')
plt.ylabel(f'{a}^b mod {n}')
plt.title(f'Modular Exponentiation Results of {a}^b mod {n}')
plt.grid(True)
plt.show()

# Test output for a specific case
specific_result = modular_exponentiation(a, 45, n)
print(f"3^45 mod 13 = {specific_result}")

Explanation of the Code

1. Modular Exponentiation Calculation:
   • The modular_exponentiation function implements the Exponentiation by Squaring algorithm.
     This method allows efficient calculation of large powers under a modulus without computing the entire number.
   • Starting with result = 1 and reducing the exponent by half in each step, we only multiply and take modulus operations.
2. Plotting Results:
   • We calculate the modular exponentiation for various values of $( b )$ (from $1$ to $45$) and store the results.
   • The plot shows $( a^b \mod n )$ on the $y$-$axis$ against the exponent $( b )$ on the $x$-$axis$, illustrating how the result changes as $( b )$ increases.

Visualization

The resulting plot shows the values of $( 3^b \mod 13 )$ for $( b = 1, 2, \ldots, 45 )$:

• The $y$-$axis$ represents the results of $( 3^b \mod 13 )$.
• Notice the cyclic behavior in the values, which is a property of modular arithmetic.

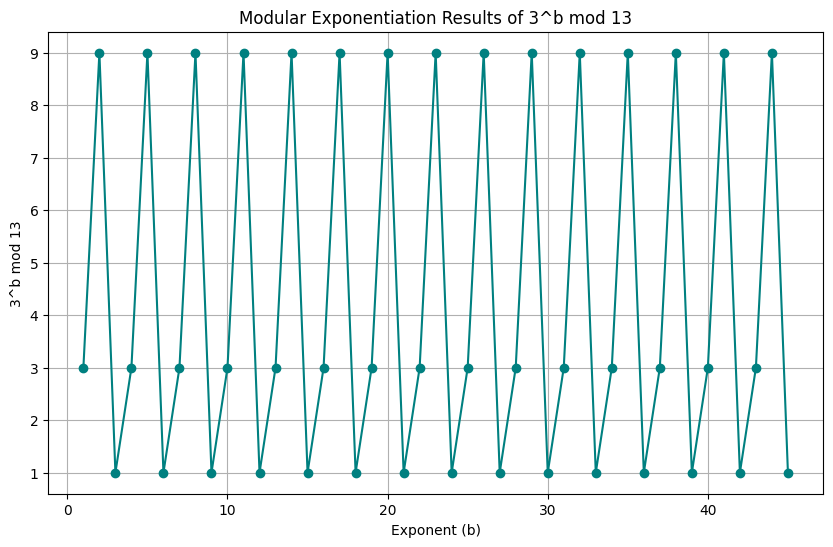
Explanation

This cyclic pattern is essential in cryptography because it enables efficient computations and helps keep the results within manageable bounds.
This property of modular arithmetic forms the basis for cryptographic systems like $RSA$, which rely on modular exponentiation for encryption and decryption.

Applications

Modular exponentiation is widely used in cryptographic systems:

• Public-Key Cryptography: Algorithms like $RSA$ and $Diffie$-$Hellman$ rely on modular exponentiation to ensure secure communication.
• Digital Signatures: Modular exponentiation is also part of signing and verifying digital messages.
• Blockchain: Modular exponentiation is employed in blockchains for secure transaction validation.

Let’s explore a discrete mathematics problem: the Fibonacci sequence, a classic example in combinatorics and discrete mathematics.

Problem: Fibonacci Sequence

The Fibonacci sequence is a series of numbers in which each number (after the first two) is the sum of the two preceding ones.

The sequence starts with 0 and 1, and is defined as follows:

$$
F(0) = 0, \quad F(1) = 1
$$
$$
F(n) = F(n-1) + F(n-2) \quad \text{for } n \geq 2
$$

The sequence goes: $0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …$

The Fibonacci sequence appears in many areas, including biology (e.g., patterns of leaves on a stem) and computer science (e.g., algorithms and data structures).

In this example, we’ll calculate the first $20$ terms of the Fibonacci sequence and visualize the results with a bar graph to illustrate the growth pattern.

Objective

Generate the first $20$ terms of the Fibonacci sequence, then plot the results to observe how the values grow as the sequence progresses.

Python Code

Here’s the Python code to calculate the Fibonacci sequence and visualize it:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import matplotlib.pyplot as plt

# Function to generate the Fibonacci sequence
def fibonacci_sequence(n):
    fib_sequence = [0, 1]
    for i in range(2, n):
        fib_sequence.append(fib_sequence[i-1] + fib_sequence[i-2])
    return fib_sequence

# Parameters
n_terms = 20  # Number of terms to generate

# Generate the Fibonacci sequence
fib_sequence = fibonacci_sequence(n_terms)

# Plot the Fibonacci sequence
plt.figure(figsize=(10, 6))
plt.bar(range(n_terms), fib_sequence, color='skyblue')
plt.xlabel('Term Index (n)')
plt.ylabel('Fibonacci Number F(n)')
plt.title('Fibonacci Sequence')
plt.xticks(range(n_terms))
plt.grid(axis='y')
plt.show()

Explanation of the Code

1. Fibonacci Sequence Generation:
   • We define a function fibonacci_sequence that generates the first n terms of the Fibonacci sequence using a loop.
   • Starting with [0, 1], we append each new term as the sum of the two previous terms.
2. Plotting the Sequence:
   • We use a bar graph to visualize the terms in the Fibonacci sequence.
   • The $x$-$axis$ represents the term index $(n)$, and the $y$-$axis$ represents the value of the Fibonacci number at that index.

Visualization

The resulting bar graph displays the first $20$ terms of the Fibonacci sequence:

• The values grow slowly at first but increase rapidly as the index gets higher, showing the characteristic exponential growth pattern of the Fibonacci sequence.
• This growth pattern illustrates how the Fibonacci sequence can approximate exponential growth, even though each term is the sum of only two preceding terms.

Applications

The Fibonacci sequence has various applications:

• Computer Science: Recursive algorithms, dynamic programming.
• Biology: Natural patterns, such as branching in trees and arrangement of leaves.
• Finance: Technical analysis in stock trading.

This example demonstrates how $Python$ can be used to solve discrete math problems and visualize sequences that exhibit interesting growth patterns.

Let’s solve a $pharmacokinetics$ problem using $Python$ and visualize the results.

$Pharmacokinetics$ is the study of how drugs move through the body, and a common problem is calculating drug concentration over time.

Problem: Drug Concentration Over Time (One-Compartment Model)

We’ll assume a single dose of a drug is administered intravenously, and it distributes uniformly throughout a single compartment in the body.

Our goal is to calculate the concentration of the drug in the bloodstream over time and plot it.

Model Assumptions

1. One-compartment model: The drug distributes instantly throughout the body.
2. First-order elimination: The drug is metabolized and eliminated at a rate proportional to its concentration.

Equations and Parameters

The concentration $(C(t))$ of the drug in the bloodstream at time $(t)$ can be calculated with:
$$
C(t) = \frac{D}{V} e^{-k \cdot t}
$$
where:

• $(D)$: The dose administered (in $mg$),
• $(V)$: The volume of distribution (in $L$),
• $(k)$: The elimination rate constant (in $1/h$), calculated as$ (k = \frac{\ln(2)}{t_{1/2}})$,
• $(t_{1/2})$: The drug’s half-life (in hours),
• $(t)$: Time after administration (in hours).

Python Code

Let’s write Python code to calculate and plot the concentration $(C(t))$ over a specified time period.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt

# Define parameters
D = 500          # Dose in mg
V = 50           # Volume of distribution in L
t_half = 4       # Half-life of the drug in hours

# Calculate the elimination rate constant
k = np.log(2) / t_half

# Time range (0 to 24 hours)
time = np.linspace(0, 24, 100)

# Calculate concentration over time
concentration = (D / V) * np.exp(-k * time)

# Plot the concentration-time curve
plt.plot(time, concentration, color='blue', label='Drug Concentration')
plt.xlabel('Time (hours)')
plt.ylabel('Concentration (mg/L)')
plt.title('Drug Concentration Over Time')
plt.grid(True)
plt.legend()
plt.show()

Explanation of the Code

1. Parameter Definitions:
   • The dose $(D)$, volume of distribution $(V)$, and half-life $(t_{1/2})$ are defined based on typical values.
2. Elimination Rate Constant:
   • We calculate $(k)$ using the half-life formula $(k = \frac{\ln(2)}{t_{1/2}})$.
3. Concentration Calculation:
   • For each time point in the defined range ($0$ to $24$ hours), we calculate the concentration $(C(t))$ using the exponential decay formula.
4. Plotting:
   • The concentration over time is plotted on a graph with time on the $x$-$axis$ and concentration on the $y$-$axis$.

Visualization

The output graph displays:

• A blue curve representing the drug concentration in the bloodstream over time.
• The concentration decreases exponentially, showing how the drug is metabolized and eliminated from the body.

This model is useful for understanding the $pharmacokinetics$ of a drug after an intravenous dose, helping in dosage planning and ensuring therapeutic levels are maintained without reaching toxic levels.

Let’s solve s geometry problem with $Python$ and visualize the result with a graph.

Here’s the problem:

Problem: Line-Circle Intersection

Given a circle and a line in a 2D plane, find the intersection points of the line and the circle, and then plot them.

Setup

1. Circle: Defined by its center $(x_c, y_c)$ and radius $(r)$.
2. Line: Defined by the linear equation $(y = mx + b)$, where $(m)$ is the slope, and $(b)$ is the y-intercept.

Solution Outline

To find the intersection points:

1. Substitute the line equation $(y = mx + b)$ into the circle equation $(x - x_c)^2 + (y - y_c)^2 = r^2$.
2. Simplify to a quadratic equation in terms of $(x)$.
3. Solve the quadratic equation:
   • If there are no real solutions, the line does not intersect the circle.
   • One real solution indicates a tangent (one intersection point).
   • Two real solutions indicate two intersection points.
4. Plot the circle, line, and intersection points.

Python Code

Here’s the $Python$ code for finding the intersection points and plotting them.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

import numpy as np
import matplotlib.pyplot as plt

def find_line_circle_intersections(xc, yc, r, m, b):
    # Solve for x in the quadratic equation
    A = 1 + m**2
    B = -2 * xc + 2 * m * (b - yc)
    C = xc**2 + (b - yc)**2 - r**2
    
    discriminant = B**2 - 4 * A * C
    
    # If discriminant is negative, no real intersection
    if discriminant < 0:
        return "No intersection"
    
    # Calculate the x-coordinates of intersection points
    x1 = (-B + np.sqrt(discriminant)) / (2 * A)
    x2 = (-B - np.sqrt(discriminant)) / (2 * A)
    
    # Calculate the corresponding y-coordinates
    y1 = m * x1 + b
    y2 = m * x2 + b
    
    return [(x1, y1), (x2, y2)] if discriminant > 0 else [(x1, y1)]

# Define the circle and line parameters
xc, yc, r = 0, 0, 5  # Circle with center (0, 0) and radius 5
m, b = 1, 1          # Line with slope 1 and y-intercept 1

# Find the intersection points
intersections = find_line_circle_intersections(xc, yc, r, m, b)

# Set up the plot
theta = np.linspace(0, 2 * np.pi, 100)
x_circle = xc + r * np.cos(theta)
y_circle = yc + r * np.sin(theta)

# Plot the circle
plt.plot(x_circle, y_circle, label='Circle', color='blue')

# Plot the line
x_vals = np.linspace(-r-2, r+2, 100)
y_vals = m * x_vals + b
plt.plot(x_vals, y_vals, label='Line', color='red')

# Plot the intersection points, if any
if intersections != "No intersection":
    for (x, y) in intersections:
        plt.plot(x, y, 'go')  # Green dots for intersection points
        plt.text(x, y, f'({x:.2f}, {y:.2f})', ha='right')

# Add labels and title
plt.xlabel('x')
plt.ylabel('y')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title('Intersection of a Circle and a Line')
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.show()

Explanation of the Code

1. Intersection Calculation:
   • The equation of the circle $(x - x_c)^2 + (y - y_c)^2 = r^2$ and the line equation $y = mx + b$ are combined.
   • Solving the resulting quadratic equation allows us to find the intersection points (if they exist).
2. Plotting:
   • The circle is drawn by parameterizing it with $(\theta)$.
   • The line is plotted using a range of $(x)$ values.
   • The intersection points (if any) are marked with green dots and labeled with their coordinates.

Visualization

The output graph displays:

• The circle and line in blue and red, respectively.
• Green dots indicate the intersection points with coordinates labeled for easy interpretation.

This graph illustrates the intersection of a circle and a line in a 2D plane.

Key Elements:

1. Circle (blue line): Centered at the origin $(0, 0)$ with a radius of $5$.
2. Line (red line): Represented by the equation $(y = x + 1)$, which has a slope of $1$ and a y-intercept of $1$.

Intersection Points:

The green dots mark the two intersection points where the line crosses the circle:

• Point 1: Located at approximately $(-4.00, -3.00)$.
• Point 2: Located at approximately $(3.00, 4.00)$.

Each point is labeled with its coordinates, making it easy to see the exact locations of intersection.

This visualization effectively shows where the line and circle meet, providing a clear solution to the problem of finding their intersection points.

To solve an optimization problem with a nonlinear objective function or nonlinear constraints in $Python$, we can use libraries like SciPy’s optimize module.

SciPy provides various functions to handle nonlinear optimization problems, including minimize with methods like 'SLSQP' (Sequential Least Squares Programming), which can handle nonlinear constraints.

In this example, we’ll set up a nonlinear objective function with a nonlinear constraint and solve it using SciPy.

Problem Setup

Suppose we want to minimize the following objective function:

$$
f(x, y) = (x - 2)^2 + (y - 1)^2
$$

This objective function represents the distance between $(x, y)$ and the point $(2, 1)$, which we aim to minimize.
We’ll also define a nonlinear constraint:

$$
g(x, y) = x^2 + y^2 - 1 \leq 0
$$

This constraint forces $(x, y)$ to lie within the unit circle centered at the origin.

Code Implementation

The following $Python$ code demonstrates how to define and solve this nonlinear optimization problem using SciPy.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

from scipy.optimize import minimize, NonlinearConstraint
import numpy as np

# Define the nonlinear objective function
def objective(vars):
    x, y = vars
    return (x - 2)**2 + (y - 1)**2

# Define the nonlinear constraint function
def constraint(vars):
    x, y = vars
    return x**2 + y**2 - 1  # This should be <= 0 to satisfy the constraint

# Create a nonlinear constraint object
nonlinear_constraint = NonlinearConstraint(constraint, -np.inf, 0)

# Initial guess for the variables
initial_guess = [0, 0]

# Solve the optimization problem
result = minimize(
    objective,
    initial_guess,
    method='SLSQP',
    constraints=[nonlinear_constraint]
)

# Display the results
if result.success:
    print("Optimal solution found:")
    print("x =", result.x[0])
    print("y =", result.x[1])
    print("Minimum value of objective function =", result.fun)
else:
    print("Optimization failed:", result.message)

Explanation of Key Components

1. Objective Function:

   • The function objective(vars) takes an array vars with variables $( x )$ and $( y )$ and returns the value of the objective function $(x - 2)^2 + (y - 1)^2$.
     This is the function we want to minimize.

2. Constraint Function:

   • The function constraint(vars) defines the constraint $( x^2 + y^2 - 1 )$, which must be less than or equal to zero for a valid solution.
     In other words, the solution must lie within or on the unit circle.

3. Nonlinear Constraint:

   • We use NonlinearConstraint to define the constraint, setting the bounds to -np.inf (no lower bound) and 0 (upper bound), which enforces $( x^2 + y^2 - 1 \leq 0 )$.

4. Optimization Solver:

   • The minimize function from SciPy is used to find the minimum of the objective function.
   • We specify method='SLSQP' to handle the nonlinear constraint, and we pass the constraint as a list.
   • The initial guess is $([0, 0])$, which serves as a starting point for the algorithm.

5. Output:

   • If successful, result.x contains the optimal values for $( x )$ and $( y )$, and result.fun gives the minimum value of the objective function.
   • If the optimization fails, an error message is displayed.

Result

Optimal solution found:
x = 0.8944272288069395
y = 0.4472135198861174
Minimum value of objective function = 1.5278640450001992

The optimization was successful, yielding an optimal solution for $( x )$ and $( y )$ within the specified constraints. The optimal values are:

• $( x = 0.894 )$
• $( y = 0.447 )$

These values minimize the objective function, achieving a minimum value of approximately $1.528$.

This result satisfies the constraint that $( x^2 + y^2 \leq 1 )$, meaning the solution lies within the unit circle as required.

Summary

This example demonstrates how to solve a constrained nonlinear optimization problem in $Python$ using SciPy.

The SLSQP algorithm in SciPy‘s minimize function is well-suited for handling nonlinear constraints and is effective for finding solutions when either the objective function or constraints are nonlinear.

Creating a 3D bubble chart in $Python$ using plotly can effectively visualize data in three dimensions, with the addition of varying bubble sizes to represent a fourth data dimension.

In this example, we’ll use plotly.graph_objects to create a Scatter3d plot where each point (or bubble) has x, y, and z coordinates along with a size attribute for the bubble’s radius.

Here’s how to create a detailed 3D bubble chart with plotly.

Step-by-Step Code Explanation

1. Generate Data: We’ll generate synthetic data for x, y, and z coordinates.
   We’ll also create a size variable to determine the size of each bubble.
2. Create a Scatter3d Plot: Using plotly.graph_objects, we’ll create a Scatter3d object to represent each bubble, where:
   • x, y, and z correspond to the spatial coordinates.
   • marker.size controls the radius of each bubble.
   • marker.color is set to vary based on another variable for an additional data layer.
3. Customize Layout: We’ll customize the layout to make the chart more informative and visually appealing.

Code Example

Here’s how you can implement a 3D bubble chart using plotly.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import numpy as np
import plotly.graph_objects as go

# Generate synthetic data
np.random.seed(0)
num_points = 100
x = np.random.normal(loc=0, scale=1, size=num_points)
y = np.random.normal(loc=1, scale=2, size=num_points)
z = np.random.normal(loc=2, scale=1.5, size=num_points)
size = np.random.randint(5, 20, size=num_points)  # Bubble sizes (can represent some other variable)

# Create a 3D scatter plot for the bubble chart
fig = go.Figure(data=[go.Scatter3d(
    x=x,
    y=y,
    z=z,
    mode='markers',
    marker=dict(
        size=size,             # Bubble sizes
        color=z,               # Color based on Z-axis values or any other metric
        colorscale='Viridis',  # Color scale for bubbles
        opacity=0.8,
        sizemode='diameter'    # Control size mode (use 'diameter' for relative sizing)
    )
)])

# Update layout for clarity
fig.update_layout(
    title="3D Bubble Chart",
    scene=dict(
        xaxis_title="X Axis",
        yaxis_title="Y Axis",
        zaxis_title="Z Axis"
    ),
    margin=dict(l=0, r=0, b=0, t=30)  # Adjust margins for better view
)

fig.show()

Explanation of Key Components

1. Data Generation: We generate random data for x, y, and z coordinates, along with a size array for bubble sizes.
   This size variable can represent any additional metric, such as population, magnitude, or frequency.

2. 3D Scatter Plot with Scatter3d:

   • x, y, and z represent the spatial coordinates.
   • marker.size controls the size of each bubble.
   • marker.color uses z values (or another variable) to set bubble colors, adding a layer of information.

3. Customization:

   • Color Scale: The Viridis color scale is used for a visually pleasing gradient effect based on z values.
   • Opacity: Setting opacity=0.8 allows overlapping bubbles to blend slightly, enhancing the 3D effect.
   • Layout: Axes are labeled, and margins are adjusted for an optimal view.

Summary

This 3D bubble chart effectively visualizes data across three spatial dimensions (x, y, and z), with the size of each bubble representing a fourth dimension.
This visualization is useful for showing multi-dimensional data, especially when analyzing clusters, correlations, or densities across multiple variables.

Visualizing complex mathematical surfaces in 3D can be incredibly insightful, especially when using interactive plotting libraries like Plotly.

In this tutorial, we’ll build an intricate 3D contour plot using plotly.graph_objects and Python’s numpy.

Although Plotly doesn’t directly support 3D contour plots, we can achieve a similar effect using the go.Surface plot type.

Let’s walk through the steps to create this visualization.

Step 1: Define a Complex Mathematical Function

To create a compelling 3D plot, we need a mathematical function that has varied, interesting features.

For this example, let’s combine trigonometric functions with an exponential decay factor.

This will produce wave-like patterns that decay outward, creating a complex and visually engaging surface.

Here’s the function we’ll use:

1
2
3
4

import numpy as np

def complex_function(x, y):
    return np.sin(x**2 + y**2) * np.exp(-0.1 * (x**2 + y**2)) + 0.5 * np.sin(3 * x) * np.cos(3 * y)

This function combines sine waves with exponential decay, resulting in a surface that has oscillations and a natural fade-out effect, adding to the complexity.

Step 2: Create a Grid of Points

We need to evaluate our function across a grid of $(x)$ and $(y)$ values.

Using numpy.linspace, we can create a finely spaced grid.

This allows us to generate smooth contours and ensures that the details of our surface are captured.

1
2
3
4

x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = complex_function(X, Y)

Here, X and Y form a 2D grid, and Z is the output of our function across this grid, representing height.

Step 3: Plot the Surface with Plotly’s go.Surface

To plot in 3D, we use Plotly’s go.Surface plot type.

go.Surface is flexible, allowing us to visualize a 3D surface with customizable color maps and contour lines.

We’ll set up contour lines along the z axis to give the appearance of a 3D contour plot.

1
2
3
4
5
6
7
8
9
10
11

import plotly.graph_objects as go

fig = go.Figure(data=go.Surface(
    x=X,
    y=Y,
    z=Z,
    colorscale='Viridis',
    contours={
        "z": {"show": True, "size": 0.1, "start": -1, "end": 1} # Define contour levels
    }
))

In this code:

• colorscale='Viridis' applies a perceptually uniform color scale, enhancing depth perception.
• contours settings add contour lines along the z axis, creating a layered effect that resembles contour lines on a topographic map.

Step 4: Customize the Layout

To make the plot more informative and visually appealing, we’ll add labels and adjust the camera view to highlight the surface’s details.

1
2
3
4
5
6
7
8
9
10
11
12

fig.update_layout(
    title="Complex 3D Contour Plot using Surface",
    scene=dict(
        xaxis_title="X Axis",
        yaxis_title="Y Axis",
        zaxis_title="Z Axis",
        camera=dict(
            eye=dict(x=1.25, y=1.25, z=0.75) # Adjust camera position for better view
        )
    )
)
fig.show()

With these settings:

• xaxis_title, yaxis_title, and zaxis_title label each axis.
• camera positions the viewpoint, giving a balanced, 3D perspective on the plot.

Full Code

Here’s the complete code to generate this 3D contour-style plot:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import numpy as np
import plotly.graph_objects as go

# Define the function for complex surface
def complex_function(x, y):
    return np.sin(x**2 + y**2) * np.exp(-0.1 * (x**2 + y**2)) + 0.5 * np.sin(3 * x) * np.cos(3 * y)

# Generate a grid of points
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = complex_function(X, Y)

# Create 3D surface plot with contours on z-axis
fig = go.Figure(data=go.Surface(
    x=X,
    y=Y,
    z=Z,
    colorscale='Viridis',
    contours={
        "z": {"show": True, "size": 0.1, "start": -1, "end": 1}
    }
))

# Customize plot
fig.update_layout(
    title="Complex 3D Contour Plot using Surface",
    scene=dict(
        xaxis_title="X Axis",
        yaxis_title="Y Axis",
        zaxis_title="Z Axis",
        camera=dict(
            eye=dict(x=1.25, y=1.25, z=0.75)
        )
    )
)

fig.show()

Output

Explanation of Key Components

• Complex Function: By combining trigonometric and exponential functions, the surface has both oscillations and decay, providing an intricate structure.
• Surface Plot and Contours: Although Plotly lacks a dedicated 3D contour plot type, adding contours on the z axis of a go.Surface plot effectively mimics this visualization style.
• Interactive Plotting: Plotly’s interactive nature allows users to explore the plot by rotating and zooming, revealing intricate details from different perspectives.

This plot is highly customizable.

Try experimenting with different functions, contour settings, and color scales to create unique 3D visualizations!

This plot simulates circular waves radiating outward from the origin.

The amplitude decays as the waves spread, creating a visually dynamic $3D$ $mesh$.

1. Import Required Libraries

First, import the necessary libraries:

1
2

import numpy as np
import plotly.graph_objects as go

2. Define the Circular Wave Grid

To create circular waves, we define a grid in polar coordinates (r for radial distance and theta for angle) and convert it to Cartesian coordinates (x and y).

This grid will form a circular, ripple-like structure.

1
2
3
4
5
6
7
8

# Define the polar grid
r = np.linspace(0, 10, 100)
theta = np.linspace(0, 2 * np.pi, 100)
r, theta = np.meshgrid(r, theta)

# Convert to Cartesian coordinates
X = r * np.cos(theta)
Y = r * np.sin(theta)

3. Define the Circular Wave Function for Z Coordinates

Define a wave function that decreases in amplitude as it moves outward.

We can use a sine function with a decaying exponential to achieve this effect:

1
2

# Circular wave function
Z = np.sin(3 * r - theta) * np.exp(-0.3 * r)

4. Reshape Data for the Mesh Plot

Flatten X, Y, and Z to 1D arrays for Plotly’s go.Mesh3d.

1
2
3

X = X.flatten()
Y = Y.flatten()
Z = Z.flatten()

5. Create the Mesh Plot

Now, create the $3D$ $mesh$ plot with customized color and transparency:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# Create the mesh plot for the circular wave
fig = go.Figure(
    data=[go.Mesh3d(
        x=X, y=Y, z=Z,
        color='blue',
        opacity=0.7,
        intensity=Z,
        colorscale="Cividis",
        alphahull=5
    )]
)

# Set layout options for a better view
fig.update_layout(
    title="3D Circular Wave Mesh Plot",
    scene=dict(
        xaxis_title='X-axis',
        yaxis_title='Y-axis',
        zaxis_title='Z-axis',
        camera=dict(
            eye=dict(x=1.5, y=1.5, z=1.5)
        )
    )
)

6. Display the Plot

To display the circular wave plot, use:

1

fig.show()

Explanation of Key Parameters

• Wave Equation: The function np.sin(3 * r - theta) * np.exp(-0.3 * r) simulates oscillations with amplitude decay, creating a wave pattern that radiates outward.
• Colorscale: The Cividis scale adds contrast, highlighting the wave peaks and valleys for a dramatic effect.
• Opacity: Lower opacity adds depth to the plot, making the wave’s radial decay easier to perceive.

This creates a visually engaging $3D$ $mesh$ that mimics ripples in water, showcasing the decaying wave amplitude as it moves outward from the origin.

Intricate 3D Surface Plot with Sine and Exponential Decay

To create a complex 3D surface plot in $Python$ using $Plotly$, we can generate a dataset that defines a surface over a grid of $x$ and $y$ values.

One common approach is to base this on mathematical functions to make the surface appear intricate, such as sinusoidal functions or $Gaussian$ surfaces, which add visually interesting layers of complexity.

Let’s walk through the steps to create a detailed 3D surface plot using $Plotly$.

1. Set Up the Libraries

First, import the required libraries:

1
2

import numpy as np
import plotly.graph_objects as go

2. Define the X and Y Grid

To create a surface, we need a grid of points for the $x$ and $y$ dimensions.

These will serve as the base coordinates for each point on our surface.

1
2
3
4

# Define the grid size
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)

3. Define the Complex Function for Z Values

For a more intricate plot, we can use a combination of functions, like a $Gaussian$ function multiplied by a sine or cosine function.

This creates peaks and valleys that look complex and engaging.

1
2

# Complex function for Z
Z = np.sin(np.sqrt(X**2 + Y**2)) * np.cos(X) * np.exp(-0.1 * np.sqrt(X**2 + Y**2))

This function combines a radial sine function with a decaying exponential, adding oscillations and smooth curvature.

4. Create the Surface Plot

With the X, Y, and Z values prepared, we use $Plotly$ to create the 3D surface plot:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# Create the surface plot
fig = go.Figure(data=[go.Surface(z=Z, x=X, y=Y, colorscale='Viridis')])

# Set additional plot parameters for enhanced aesthetics
fig.update_layout(
    title="Complex 3D Surface Plot",
    scene=dict(
        xaxis_title='X-axis',
        yaxis_title='Y-axis',
        zaxis_title='Z-axis',
        camera=dict(
            eye=dict(x=1.25, y=1.25, z=1.25)
        ),
        aspectratio=dict(x=1, y=1, z=0.5)
    )
)

5. Display the Plot

Finally, display the plot with:

1

fig.show()

Explanation of the Parameters

• Colorscale: Viridis is chosen for its high-contrast, which enhances the readability of peaks and valleys.
  You can try others like Plasma or Cividis.
• Scene settings: This includes axis titles for clarity and a custom camera position to provide a good viewing angle.
• Aspect ratio: Adjusts the scaling of the axes, so the plot is not distorted.

This script generates a 3D surface that features smooth transitions, sharp peaks, and interesting valleys, making it a complex and visually appealing 3D plot.

Adjusting the function or grid size can add further complexity if desired.

$Plotly$’s 3D scatter plot capabilities allow us to visualize complex, multi-dimensional data interactively.

We’ll create a detailed 3D scatter plot with customizations such as color-coding, sizing, and axis labels.

This example demonstrates how to plot complex data with customized markers, informative labels, and meaningful axes, all designed to enhance clarity and interaction with the data.

We’ll use synthetic data that includes three main dimensions, X, Y, and Z, representing each axis in the 3D space, and additional features that determine point colors and sizes.

Step-by-Step Explanation and Code

1. Generate Data:
   We’ll create synthetic data using $NumPy$ to represent our 3D points, with values for each axis (X, Y, Z) and two additional variables (category for color and size for marker size).

2. Set Up the Plotly 3D Scatter Plot:
   Using $Plotly$’s go.Scatter3d, we’ll customize our 3D plot to visualize:

   • Point Colors: Categorical values will be represented by different colors.
   • Point Sizes: A continuous variable will determine the size of each point.
   • Axis Titles: Labels for each axis to provide clear context.

3. Customize Layout:
   We’ll adjust the layout to add titles, background, and enhance interactivity.

Here’s the $Python$ code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import plotly.graph_objects as go
import numpy as np

# Generate synthetic data
np.random.seed(42)
n_points = 200
x = np.random.uniform(0, 100, n_points)  # X values
y = np.random.uniform(0, 100, n_points)  # Y values
z = np.random.uniform(0, 100, n_points)  # Z values
category = np.random.choice(['Category A', 'Category B', 'Category C'], n_points)  # Color by category
size = np.random.uniform(5, 20, n_points)  # Size variable for marker size

# Map categories to colors
color_map = {'Category A': 'red', 'Category B': 'blue', 'Category C': 'green'}
colors = [color_map[cat] for cat in category]

# Create the 3D scatter plot
fig = go.Figure(
    data=[
        go.Scatter3d(
            x=x,
            y=y,
            z=z,
            mode='markers',
            marker=dict(
                size=size,
                color=colors,
                opacity=0.8,
                line=dict(width=1, color='DarkSlateGrey')
            ),
            text=[f"X: {x_val:.2f}, Y: {y_val:.2f}, Z: {z_val:.2f}, Size: {size_val:.2f}" 
                  for x_val, y_val, z_val, size_val in zip(x, y, z, size)],
            hoverinfo='text'
        )
    ]
)

# Customize the layout
fig.update_layout(
    title="3D Scatter Plot with Color and Size Encoding",
    scene=dict(
        xaxis=dict(title="X Axis (e.g., Feature 1)"),
        yaxis=dict(title="Y Axis (e.g., Feature 2)"),
        zaxis=dict(title="Z Axis (e.g., Feature 3)"),
        bgcolor="rgba(240,240,240,0.95)"
    ),
    width=800,
    height=600,
    showlegend=False
)

fig.show()

Detailed Explanation

1. Data Generation:

   • We use $NumPy$’s np.random.uniform to generate random values for X, Y, and Z coordinates within a specified range.
     We also define category (with values like Category A, Category B, Category C) and size, which affects the marker sizes.
   • We assign colors using color_map, where each category has a different color (e.g., red, blue, green).

2. Creating the Scatter Plot:

   • Scatter3d: This $Plotly$ function is used to create 3D scatter plots.
     x, y, and z are assigned to the respective coordinate values.
   • Marker Customization:
     • size=size adjusts the size of each marker based on the size variable.
     • color=colors assigns colors based on the category.
     • opacity=0.8 provides transparency, making overlapping points more distinguishable.
     • line=dict(width=1, color='DarkSlateGrey') adds a border to each marker, improving visibility.
   • Hover Information: We provide custom hover text to display values for X, Y, Z, and size when hovering over points.

3. Layout Customization:

   • title provides a clear title for the plot.
   • Axis Titles: Each axis is labeled to describe the corresponding feature.
   • Background Color: scene.bgcolor is set to a light grey, which enhances the visibility of the colored points.
   • Dimensions: We specify width and height for consistent display.

Interpretation

This interactive 3D scatter plot allows us to observe:

• Distribution: The spread of points across the three dimensions reveals clustering patterns and possible outliers.
• Category Comparison: Colors represent different categories, allowing us to compare distributions between them.
• Point Emphasis: Size variation highlights differences in another variable, helping us to see patterns across categories or regions of the 3D space.

Output

The resulting plot will display a 3D scatter plot with different colors for each category, sizes reflecting a separate feature, and axis titles.

This interactive view lets you rotate, zoom, and hover over points for detailed insights.

Conclusion

The 3D scatter plot with $Plotly$ provides a powerful way to explore complex, multi-variable relationships in data.

By encoding multiple variables in position, color, and size, we can convey a rich amount of information in a single, interactive plot, ideal for data science, research, and presentation purposes.