気候データの予測

Prophetを使用して気候データの予測を行うことは一般的です。

以下は、気温の予測を例に示します。

Prophetを使用して気温データを予測し、結果をグラフ化する方法です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 必要なライブラリをインポート
import pandas as pd
from prophet import Prophet
import matplotlib.pyplot as plt

# サンプル気温データを定義
data = pd.DataFrame({
    'ds': ['2023-01-01', '2023-01-02', '2023-01-03', '2023-01-04', '2023-01-05'],
    'y': [10.5, 11.2, 12.1, 9.8, 10.3]
})

# Prophetモデルの作成
model = Prophet()

# データに適合させる
model.fit(data)

# 予測用の未来の日付を生成
future = model.make_future_dataframe(periods=30)

# 予測を実行
forecast = model.predict(future)

# 予測結果をグラフ化
fig = model.plot(forecast)
plt.title('Temperature Forecast')
plt.xlabel('Date')
plt.ylabel('Temperature (°C)')
plt.show()

この例では、5日間のサンプル気温データを使用してProphetモデルを訓練し、将来の30日間の気温を予測しています。

ソースコード解説

以下は、ソースコードの各部分の詳細説明です。

1. 必要なライブラリをインポートします:

• pandas: データを扱うためのライブラリ。
• Prophet: 時系列データの予測を行うためのProphetモデルを提供するライブラリ。
• matplotlib.pyplot: グラフを描画するためのライブラリ。

2. サンプル気温データを定義します:

• data データフレームには、日付 (ds) と気温 (y) の2つの列があります。
  これはProphetモデルに渡すためのサンプルデータです。このサンプルでは、5つの日付とそれに対応する気温が提供されています。

3. Prophetモデルを作成します:

• Prophet() コンストラクタを使用してProphetモデルを作成します。

4. データに適合させます:

• model.fit(data) を呼び出して、Prophetモデルを提供されたデータに適合させます。
  これにより、モデルはデータのトレンドや季節性を学習します。

5. 予測用の未来の日付を生成します:

• model.make_future_dataframe(periods=30) を呼び出して、将来の日付を含むデータフレームを生成します。
  periods パラメータは、いくつの未来の日付を生成するかを指定します。
  この例では30日間の未来の日付を生成しています。

6. 予測を実行します:

• model.predict(future) を呼び出して、未来の気温を予測します。
  この予測結果は forecast データフレームに格納されます。

7. 予測結果をグラフ化します:

• model.plot(forecast) を呼び出して、予測結果をグラフ化します。
  x軸に日付、y軸に気温が表示され、青い線は予測された気温のトレンドを表し、灰色の領域は予測の信頼区間を示します。
  また、グラフにタイトルと軸ラベルも追加されています。

このソースコードはProphetを使用して気温データの予測を行い、結果をグラフで視覚化する基本的なスクリプトです。

データと期間を変更すれば、他の時系列データに対しても同様の予測を行うことができます。

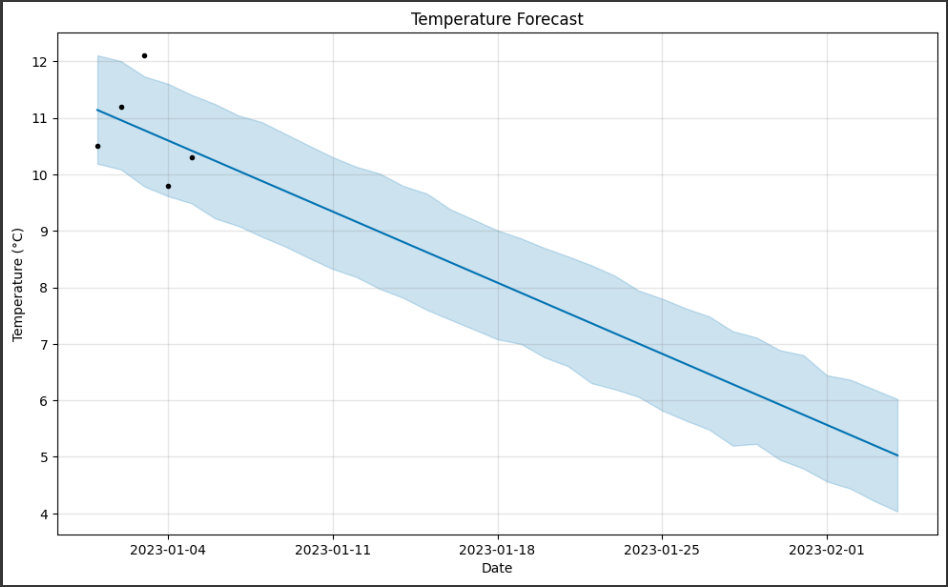
グラフ解説

Prophetによって生成されたグラフは、時間軸に沿った気温データの予測とその信頼区間を示しています。

以下に、このグラフの詳細を説明します。

1. 黒いポイント:

黒いポイントは実際のデータポイントです。

2. 青い線:

青い線はトレンドの予測の一部で、気温の変動のトレンドを表します。

3. 水色の領域:

水色の領域は予測の信頼区間を示しています。
通常、Prophetは予測の不確実性を示すためにこの信頼区間を提供します。
水色の領域の幅が広ければ広いほど、不確実性が高いことを示します。

4. x軸 (Date):

時間軸は日付を示しており、過去のデータから将来の日付に向かって予測が行われています。

5. y軸 (Temperature):

y軸は気温を示しており、単位は摂氏度（°C）です。これは気温の値が表示されます。

このグラフは、Prophetモデルによる気温の予測を視覚化するためのものであり、予測された気温のトレンド、季節性、信頼区間などを理解するのに役立ちます。

例えば、将来の日付における気温の予測傾向や変動の不確実性を把握することができます。

飛行距離

空気抵抗を無視した水平投射の物体の飛行距離を計算し、速度に対する飛行距離の関係をグラフ化します。

物体の水平投射の飛行距離 $ (D) $ は以下の式で表されます。

$$
[ D = \frac{v^2 \sin(2\theta)}{g} ]
$$

[単位説明]

• $ (D) $ は飛行距離（メートル）
• $ (v) $ は初速度（$ m/s $）
• $ (\theta) $ は発射角度（ラジアン）
• $ (g) $ は重力加速度（$ 約9.81 m/s^2 $）

この関数をSciPyを使用して計算し、初速度に対する飛行距離の関係をグラフ化します。

以下がPythonコードの例です：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import numpy as np
import matplotlib.pyplot as plt

# 重力加速度 (m/s^2)
g = 9.81

# 発射角度 (ラジアン)
theta = np.pi / 4  # 45度

# 初速度の範囲を設定
v_values = np.linspace(0, 100, 100)  # 0から100 m/sまで100点でサンプリング

# 飛行距離を計算する関数
def calculate_distance(v):
    return (v**2 * np.sin(2 * theta)) / g

# 初速度に対する飛行距離を計算
distances = [calculate_distance(v) for v in v_values]

# 飛行距離 vs 初速度のグラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(v_values, distances)
plt.title('Flight Distance vs Initial Velocity')
plt.xlabel('Initial Velocity (m/s)')
plt.ylabel('Flight Distance (meters)')
plt.grid(True)
plt.show()

このコードは、初速度に対する飛行距離の関係を示すグラフを生成します。

グラフは初速度が増加するにつれて、飛行距離も増加することを示しています。

ソースコード解説

このソースコードは、初速度に対する飛行距離の関係を計算し、それをグラフ化するためのPythonプログラムです。

以下にソースコードの詳細な説明を提供します：

1. import numpy as npとimport matplotlib.pyplot as plt：

NumPyとMatplotlibライブラリをインポートします。
NumPyは数値計算のために使用され、Matplotlibはグラフの描画に使用されます。

2. g = 9.81：

重力加速度を表す変数 g を設定します。この値は約$9.81 m/s^2$で、地球上での標準的な重力加速度です。

3. theta = np.pi / 4：

発射角度をラジアンで表す変数 theta を設定します。
ここでは45度をラジアンに変換しています。
ラジアンは角度を表す単位で、$ ( \pi ) $ ラジアンは$180$度です。

4. v_values = np.linspace(0, 100, 100)：

初速度の範囲を設定します。
np.linspace関数を使用して、$ 0 $ から $ 100 m/s $ までの初速度を$100$点でサンプリングした配列 v_values を生成します。
これにより、初速度の値が $ 0 $ から $ 100 $ まで均等に分布する配列が作成されます。

5. def calculate_distance(v)：

初速度 (v) を受け取って飛行距離を計算する関数 calculate_distance を定義します。
計算式は先ほど説明した通りです。

6. distances = [calculate_distance(v) for v in v_values]：

各初速度に対する飛行距離を計算し、リスト distances に格納します。
リスト内包表記を使用して、各初速度に対して関数 calculate_distance を呼び出して計算します。

7. plt.figure(figsize=(8, 6))：

Matplotlibで新しい図を作成し、図のサイズを設定します。

8. plt.plot(v_values, distances)：

初速度 (v_values) に対する飛行距離 (distances) のグラフをプロットします。
これにより、初速度に対する飛行距離の関係が表示されます。

9. plt.title('Flight Distance vs Initial Velocity')：

グラフにタイトルを追加します。

10. plt.xlabel('Initial Velocity (m/s)')：

x軸（横軸）にラベル “Initial Velocity (m/s)” を追加します。

11. plt.ylabel('Flight Distance (meters)')：

y軸（縦軸）にラベル “Flight Distance (meters)” を追加します。

12. plt.grid(True)：

グリッド線を表示します。

13. plt.show()：

グラフを表示します。
これにより、初速度と飛行距離の関係を視覚的に確認できます。

このソースコードは、初速度と飛行距離の関係を探るために、初速度の範囲をサンプリングし、飛行距離を計算してグラフ化するシンプルな物理学の問題を解決するためのものです。

グラフ解説

下記のグラフは、初速度に対する飛行距離の関係を示しています。

以下にこのグラフの詳細な説明を提供します。

1. x軸（初速度）:

グラフの横軸は初速度（$(v)$）を表しています。
初速度は水平方向に物体を投射する速度で、単位はメートル毎秒$（m/s）$です。
x軸は0から100 m/sまでの初速度の範囲をカバーしています。

2. y軸（飛行距離）:

グラフの縦軸は飛行距離 $ (D)） $ を表しています。
飛行距離は物体が水平方向にどれだけ進むかを示し、単位もメートル $ （m） $ です。

3. グラフの形状:

グラフは放物線の形状をしています。
これは初速度が増加するにつれて飛行距離が増加することを示しています。
初速度が低い場合、物体は遠くまで飛びませんが、初速度が高い場合、物体は遠くまで飛びます。

4. 最大飛行距離:

グラフ上で最大の飛行距離は、放物線の頂点に対応します。
この最大値は特定の初速度で達成され、最大飛行距離を得るためにはその初速度で物体を投射する必要があります。

5. 角度 $ (\theta) $ の影響:

グラフは特定の発射角度（この例では $ 45 $ 度または $ (\pi/4) $ ラジアン）を想定しています。
発射角度が異なる場合、最大飛行距離の値や初速度での発射条件が変化します。
したがって、発射角度を変えるとグラフの形状も変化します。

このグラフは、物理的な問題で初速度と飛行距離の関係を視覚化するのに役立ちます。

初速度を調整することで、特定の飛行距離を達成したり、最大飛行距離を求めたりするのに役立つ情報を提供しています。

クレジットカード詐欺検出

クレジットカード詐欺検出は、信用カード取引の中から不正な取引を検出する重要な問題です。

以下では、サポートベクターマシン（SVM）を使用してクレジットカード詐欺を検出するモデルを構築する例を示します。

この問題に取り組むために、Kaggleなどから入手できるクレジットカード詐欺のデータセットを使用します。

（googleで“card_transdata.csv”という単語で検索すると、検索結果の１番目に表示されます。）

データの前処理、モデルトレーニング、評価などのステップが含まれています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

# クレジットカード詐欺データセットの読み込み（実際のデータセットを使用する必要があります）
# データセットはCSVファイルと仮定しています
data = pd.read_csv('card_transdata.csv')

# 特徴量とラベルの分割
X = data.drop('Class', axis=1)
y = data['Class']

# データの前処理 (スケーリング)
scaler = StandardScaler()
X = scaler.fit_transform(X)

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# サポートベクターマシン (SVM) モデルの作成
svm_model = SVC(kernel='linear', C=1, random_state=42)

# モデルの学習
svm_model.fit(X_train, y_train)

# テストデータで評価
y_pred = svm_model.predict(X_test)

# 分類精度の計算
accuracy = accuracy_score(y_test, y_pred)
print("分類精度:", accuracy)

# 混同行列の表示
confusion = confusion_matrix(y_test, y_pred)
print("混同行列:\n", confusion)

# 分類レポートの表示
classification_rep = classification_report(y_test, y_pred)
print("分類レポート:\n", classification_rep)

このコードでは、クレジットカード詐欺のデータセットを使用して、SVMモデルをトレーニングし、評価します。

評価には分類精度、混同行列、分類レポートが使用されます。

[実行結果]

1
2
3
4
5
6
7
8
9
10
11
12
13

分類精度: 0.961565
混同行列:
 [[181235   1322]
 [  6365  11078]]
分類レポート:
               precision    recall  f1-score   support

         0.0       0.97      0.99      0.98    182557
         1.0       0.89      0.64      0.74     17443

    accuracy                           0.96    200000
   macro avg       0.93      0.81      0.86    200000
weighted avg       0.96      0.96      0.96    200000

クレジットカード詐欺検出は、不正な取引を検出するための重要なアプリケーションであり、機械学習モデルを使用してセキュリティを向上させるのに役立ちます。

ソースコード解説

ソースコードの各部分を詳しく説明します。

1. ライブラリのインポート:

1
2
3
4
5
6

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

必要なライブラリをインポートしています。
Pandasはデータフレーム操作のために、NumPyは数値計算のために使用されます。

train_test_splitはデータセットをトレーニングデータとテストデータに分割するために使用し、StandardScalerはデータのスケーリングを行います。

SVCはサポートベクターマシン（Support Vector Machine）モデルのためのクラスです。

accuracy_score、confusion_matrix、classification_reportはモデルの評価指標を計算するために使用されます。

2. データセットの読み込み:

1

data = pd.read_csv('card_transdata.csv')

データセットをCSVファイルから読み込みます。

データセットは提供されたデータで、クレジットカード取引に関する情報を含んでいます。

3. 特徴量とラベルの分割:

1
2

X = data.drop('fraud', axis=1)
y = data['fraud']

データセットを特徴量（説明変数）とラベル（ターゲット変数）に分割します。

Xには'fraud'列以外の特徴量が含まれ、yには詐欺かどうかを示すラベルが含まれます。

4. データの前処理 (スケーリング):

1
2

scaler = StandardScaler()
X = scaler.fit_transform(X)

特徴量データ X を標準化（平均0、分散1にスケーリング）します。

標準化は多くの機械学習アルゴリズムで重要です。

5. データの分割:

1

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

データをトレーニングデータとテストデータに分割します。

test_size=0.2 は、データの20%をテストデータに割り当てることを意味します。

random_stateは乱数のシードを設定し、再現性を確保します。

6. サポートベクターマシン (SVM) モデルの作成:

1

svm_model = SVC(kernel='linear', C=1, random_state=42)

サポートベクターマシン（SVM）モデルを作成します。

ここでは線形カーネル (kernel='linear') を使用し、正則化パラメータ C は1に設定しています。

7. モデルの学習:

1

svm_model.fit(X_train, y_train)

作成したSVMモデルをトレーニングデータで学習させます。

8. テストデータで評価:

1

y_pred = svm_model.predict(X_test)

学習済みモデルを使用してテストデータに対する予測を行います。

9. 分類精度

の計算:

1
2

accuracy = accuracy_score(y_test, y_pred)
print("分類精度:", accuracy)

分類精度を計算し、テストデータに対するモデルの性能を評価します。

10. 混同行列 (Confusion Matrix) の表示:

1
2

confusion = confusion_matrix(y_test, y_pred)
print("混同行列:\n", confusion)

混同行列は、真陽性、真陰性、偽陽性、偽陰性のカウントを示す表です。

モデルの性能を評価するのに役立ちます。

11. 分類レポート (Classification Report) の表示:

1
2

classification_rep = classification_report(y_test, y_pred)
print("分類レポート:\n", classification_rep)

分類レポートには、精度、再現率、F1スコアなど、さまざまな評価指標が含まれています。

モデルの詳細な性能評価を提供します。

結果解説

それぞれの評価指標について詳しく説明します。

1. 分類精度 (Accuracy): 0.961565

• 分類精度は、モデルが正確にクレジットカード取引を詐欺と非詐欺に分類した割合を示します。
  このモデルは、与えられたテストデータ全体の96.16%の正確性でクレジットカード取引を分類できることを示しています。
  高い分類精度は、モデルがほとんどの取引を正しく識別していることを示しています。

2. 混同行列 (Confusion Matrix):

1
2

[[181235   1322]
 [  6365  11078]]

• 混同行列は、モデルの予測と実際のクレジットカード取引ラベルとの関係を示します。
• 左上のセル (181235) は真陰性（Non-fraudを正しく予測）の数を示します。
• 右上のセル (1322) は偽陽性（Non-fraudを誤って詐欺と予測）の数を示します。
• 左下のセル (6365) は偽陰性（Fraudを誤って非詐欺と予測）の数を示します。
• 右下のセル (11078) は真陽性（Fraudを正しく詐欺と予測）の数を示します。

3. 分類レポート (Classification Report):

1
2
3
4
5
6
7
8

               precision    recall  f1-score   support

         0.0       0.97      0.99      0.98    182557
         1.0       0.89      0.64      0.74     17443

    accuracy                           0.96    200000
   macro avg       0.93      0.81      0.86    200000
weighted avg       0.96      0.96      0.96    200000

• 分類レポートは、クレジットカード詐欺検出モデルの詳細な評価指標を提供します。
• precision（適合率）は、モデルが詐欺と予測した取引のうち、実際に詐欺である割合を示します。
  詐欺の適合率は0.89であり、比較的高いです。
• recall（再現率）は、実際に詐欺である取引のうち、モデルが正しく詐欺と予測した割合を示します。
  詐欺の再現率は0.64であり、詐欺を見逃す可能性があることを示しています。
• f1-score（F1スコア）は、適合率と再現率の調和平均であり、モデルのバランスを評価します。
  詐欺のF1スコアは0.74で、適合率と再現率のトレードオフを示します。
• supportは各クラス（詐欺と非詐欺）のサポート数を示します。
• accuracy（正解率）は、正確な予測の割合を示し、先に述べた通り0.961565です。
• macro avgおよびweighted avgは、クラスごとの平均と重み付け平均を示します。
  通常、クラスのバランスが異なる場合にはweighted avgが重要です。

この結果から、モデルは非詐欺取引の予測に優れた性能を示しており、高い分類精度を持っていますが、詐欺の検出には改善の余地があることがわかります。

最適化問題

問題: 線形制約を持つ最適化問題を解決して、最適な解を見つけましょう。

次のような最適化問題を考えます：

$$
最小化 \quad f(x) = x_1^2 + 2x_2^2 + 3x_3^2
$$

以下の制約条件が存在します：

$$
\begin{align*}
2x_1 + x_2 - x_3 & \geq 1 \\
x_1 + 3x_2 + 2x_3 & \leq 4 \\
x_1, x_2, x_3 & \geq 0
\end{align*}
$$

この最適化問題をSciPyを使用して解決し、最適な解を見つけ、結果を分かりやすくグラフ化します。

以下は、この問題を解決するPythonコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 目的関数を定義
def objective_function(x):
    return x[0]**2 + 2*x[1]**2 + 3*x[2]**2

# 制約条件を定義
constraints = (
    {'type': 'ineq', 'fun': lambda x: 2*x[0] + x[1] - x[2] - 1},
    {'type': 'ineq', 'fun': lambda x: -x[0] - 3*x[1] - 2*x[2] + 4}
)

# 初期推定値を設定
initial_guess = [1, 1, 1]

# 最適化アルゴリズムを使用して最小値を探索
result = minimize(objective_function, initial_guess, constraints=constraints)

# 最小値と最適な解を取得
minimum_value = result.fun
optimal_x = result.x

# 結果の表示
print(f"最小値: {minimum_value}")
print(f"最適な解: {optimal_x}")

# 最適化問題のグラフ化
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 目的関数の3Dプロット
x1 = np.linspace(0, 2, 100)
x2 = np.linspace(0, 2, 100)
x1, x2 = np.meshgrid(x1, x2)
x3 = (2*x1 + x2 - 1)

ax.plot_surface(x1, x2, objective_function([x1, x2, x3]), cmap='viridis', alpha=0.8)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x)')
ax.set_title('Objective Function of Optimization Problem')

# 制約条件のプロット
x1 = np.linspace(0, 2, 100)
x2 = np.linspace(0, 2, 100)
x1, x2 = np.meshgrid(x1, x2)
x3 = (2*x1 + x2 - 1)
ax.plot_surface(x1, x2, x3, color='red', alpha=0.5, linewidth=0, antialiased=False)

plt.show()

このコードは、目的関数 $ (f(x) = x_1^2 + 2x_2^2 + 3x_3^2) $ を最小化するための線形制約を持つ最適化問題を解決し、結果を3Dプロットで視覚化します。

制約条件を満たす範囲内で、最適な解を見つけるためにSciPyの最適化ツールが使用されます。

ソースコード解説

ソースコードの各部分を説明します。

1. ライブラリのインポート:

• numpyは数値計算用のライブラリで、数値配列の操作に使用されます。
• matplotlib.pyplotはグラフを描画するためのライブラリで、グラフの可視化に使用されます。
• scipy.optimize.minimizeは、最適化問題を解決するための関数を提供するSciPyライブラリからインポートされています。

2. 目的関数の定義:

• objective_functionという関数が定義されています。この関数は、最小化したい目的関数を表します。ここでは次の目的関数を使用しています。

  1	f(x) = x[0]^2 + 2*x[1]^2 + 3*x[2]^2

  この関数は3つの変数（x0、x1、x2）に依存しており、これらの変数の値を入力として受け取ります。

3. 制約条件の定義:

• constraintsは、制約条件を表すリストです。各制約は辞書として表されており、'type'キーで制約の種類（不等式制約）を指定し、'fun'キーで制約関数を指定します。
• 2つの制約条件が定義されています。1つは不等式制約 2*x[0] + x[1] - x[2] - 1 >= 0、もう1つは不等式制約 -x[0] - 3*x[1] - 2*x[2] + 4 <= 0 です。

4. 初期推定値の設定:

• initial_guessは、最適化アルゴリズムの初期値を設定するリストです。ここでは [1, 1, 1] と設定されています。

5. 最適化アルゴリズムの実行:

• minimize関数を使用して最適化アルゴリズムを実行します。この関数には目的関数、初期推定値、および制約条件が渡されます。
• アルゴリズムは最小値を見つけ、結果をresultに格納します。

6. 最小値と最適な解の表示:

• 最適化の結果、最小値（最適な目的関数の値）と最適な解（x0、x1、x2の値）を取得し、それらを表示します。

7. 最適化問題のグラフ化:

• 3Dプロットを作成し、目的関数と制約条件を視覚化します。
• 目的関数の3Dプロットと制約条件の領域が描かれ、最適な解がどこにあるかがわかります。

このソースコードは、数値最適化の基本的な例を示しており、制約条件を持つ最適化問題を解決し、結果を可視化する方法を示しています。

目的関数と制約条件が異なる場合、このコードを適応させて問題を解決できます。

グラフ解説

結果として表示されるグラフは、3Dプロットを使用して最適化問題の目的関数と制約条件を視覚化するものです。

このグラフの詳細な説明を提供します。

1. 目的関数の3Dプロット:

• グラフの上半分は、目的関数 $ (f(x) = x_1^2 + 2x_2^2 + 3x_3^2) $ の3Dプロットです。
• $ x1, x2, x3 $ の値に対して、目的関数の値（$ f(x)）$ がプロットされています。
• $ x1, x2, x3 $ の値域はそれぞれ $ 0 $ から $ 2 $ までです。
• 目的関数は放物面の形状を持ち、下に凹んでいることがわかります。
  つまり、最小値が存在します。

2. 制約条件のプロット:

• グラフの下半分は、制約条件 $ (2x_1 + x_2 - x_3 \geq 1) $ と $ (-x_1 - 3x_2 - 2x_3 \leq 4) $ のプロットです。
• 制約条件を満たすために許容される領域が赤で示されています。
  この領域内で解を見つける必要があります。

3. 最適な解の表示:

• 最適な解は、目的関数の最小値を示す点であり、その位置は赤で示されています。
• 最適な解は目的関数を最小化するために制約条件を満たす範囲内で見つけられた点です。

このグラフは、最適化問題の可視化に役立ちます。

目的関数の最小値を見つけるために、制約条件を満たす範囲内で最適な解を探す必要があります。

赤で示されている領域内で目的関数を最小化する点が、最適な解となります。

このような視覚化を使用することで、最適化問題を直感的に理解し、解を探すのに役立ちます。

製造計画の最適化問題

PuLPを使用して製造計画の最適化問題を提供します。
この問題は、多くの制約条件を考慮に入れた複雑な最適化問題です。

問題: ある製造会社が複数の製品を生産する製造計画を最適化します。
各製品の生産には材料、労働力、設備の制約があり、目標は製品の利益を最大化する最適な生産計画を見つけることです。
さらに、生産計画は以下の制約条件を満たす必要があります。

1. 各製品ごとの最小生産量および最大生産量がある。
2. 材料の在庫レベルと設備の容量制約がある。
3. 労働力の制約があり、1つのシフトでの最大労働時間が制限されている。

以下は、この問題をPuLPを使用して解決するPythonコードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 必要なライブラリのインポート
import pulp

# 問題の初期化
problem = pulp.LpProblem("Production_Optimization", pulp.LpMaximize)

# 製品ごとの生産量変数を定義
x1 = pulp.LpVariable("Product1_Production", lowBound=100, upBound=500, cat="Integer")
x2 = pulp.LpVariable("Product2_Production", lowBound=50, upBound=300, cat="Integer")

# 目的関数を定義: 利益を最大化
profit = 10 * x1 + 15 * x2
problem += profit, "Total_Profit"

# 制約条件を定義
# 材料制約
material_constraint1 = 2 * x1 + 3 * x2 <= 1200
problem += material_constraint1, "Material_Constraint1"
material_constraint2 = 4 * x1 + 2 * x2 <= 1600
problem += material_constraint2, "Material_Constraint2"

# 労働力制約
labor_constraint = 4 * x1 + 6 * x2 <= 2400
problem += labor_constraint, "Labor_Constraint"

# 設備制約
equipment_constraint = 3 * x1 + 2 * x2 <= 1500
problem += equipment_constraint, "Equipment_Constraint"

# 最適化を実行
problem.solve()

# 結果を表示
print("最適化結果:")
for var in problem.variables():
    print(f"{var.name} = {var.varValue}")

print(f"最適な利益 = ${pulp.value(problem.objective)}")

このコードは、PuLPを使用して製造計画を最適化する例です。
製品ごとの生産量を最適化し、利益を最大化するための制約条件を考慮しています。
最適な生産量と最適な利益を表示しています。

[実行結果]

1
2
3
4

最適化結果:
Product1_Production = 300.0
Product2_Production = 200.0
最適な利益 = $6000.0

この問題は、複雑な生産計画を最適化する方法を示しており、実際の製造業務で役立つかもしれません。

制約条件やパラメータを調整して、特定の製造環境に合わせた最適化計画を見つけることができます。

ソースコード解説

ソースコードの各部分を詳しく説明します。

1. 必要なライブラリのインポート:

まず、PuLPを使用するために必要なライブラリをインポートします。

2. 問題の初期化:

pulp.LpProblem を使用して、最適化問題を初期化します。
この問題は、最大化（pulp.LpMaximize）される利益を最大化する問題です。

3. 製品ごとの生産量変数を定義:

pulp.LpVariable を使用して、製品1（x1）と製品2（x2）の生産量を変数として定義します。
lowBound と upBound パラメータを使用して、それぞれの変数の最小値と最大値を設定し、cat="Integer" で整数値であることを指定します。

4. 目的関数を定義:

profit 変数を定義し、この変数を最大化することを目指します。
利益は、製品1の生産量と製品2の生産量に対する係数をかけたものです。
このようにして、目標となる利益を設定します。

5. 制約条件を定義:

製造プロセスにはいくつかの制約条件があります。
これらの制約条件は、各製品の材料、労働力、設備などの制約を表します。
それぞれの制約条件は、不等式として定義されます。
たとえば、material_constraint1 は製品1と製品2の材料の制約を表しており、2 * x1 + 3 * x2 が 1200 以下である必要があります。

6. 最適化を実行:

problem.solve() を呼び出して最適化を実行します。
PuLPは、線形計画法を使用して最適な変数の値を見つけます。

7. 結果を表示:

最適化の結果、各変数（製品1と製品2の生産量）の最適な値が表示されます。
また、pulp.value(problem.objective) を使用して最適な利益を計算し、表示します。

このコードは、製造計画を最適化するための一般的なスクリプトの例であり、特定の制約条件や利益計算式をカスタマイズして、異なる製造計画の最適化問題に適用できます。

結果解説

最適化結果は以下のようになりました。

[実行結果]

1
2
3
4

最適化結果:
Product1_Production = 300.0
Product2_Production = 200.0
最適な利益 = $6000.0

詳細を説明します。

1. Product1_Production = 300.0:

この結果は、製品1の生産量が300単位であることを示しています。
つまり、製品1を300個生産することが最適とされました。

2. Product2_Production = 200.0:

この結果は、製品2の生産量が200単位であることを示しています。
つまり、製品2を200個生産することが最適とされました。

3. 最適な利益 = $6000.0:

最適な利益は、製造計画を最適化した結果の利益を示しています。
最適な製品生産量を設定した場合、企業は合計で$6000の利益を得ることができるということです。

この結果は、製品の生産と利益を最大化するための最適な戦略を示しています。

製品ごとの生産量は、材料、労働力、設備などの制約条件を満たす範囲で決定され、最終的に利益が最大化されました。

企業はこの最適な生産計画に従って製造プロセスを調整し、$6000の利益を実現することができます。

化学反応の速度

ある化学反応があるとき、反応速度が時間とともにどのように変化するかを予測したいとします。

具体的には、1次反応（一般的な化学反応のタイプの一つ）を考えます。

まず、必要なライブラリと関数をインポートします。

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

次に、反応速度定数（$k$）と初濃度（初量）を設定します。

1
2
3
4
5
6
7
8

# 反応速度定数 (1/s)
k = 0.1

# 初濃度 (mol/L)
C0 = 1.0

# 時間の範囲 (秒)
t = np.linspace(0, 50, 100)

次に、反応速度を表す微分方程式を定義します。

1
2
3
4

# 反応速度を表す微分方程式の定義
def model(C, t):
    dCdt = -k * C  # dC/dt = -k * C (1次反応の微分方程式)
    return dCdt

次に、odeintを使用して微分方程式を数値的に解きます。

1
2
3
4
5
6
7
8

# 初期条件
initial_condition = C0

# 微分方程式を解く
solution = odeint(model, initial_condition, t)

# 解から濃度を取得
concentration = solution[:, 0]

最後に、濃度と時間の関係をグラフに表示します。

1
2
3
4
5
6
7
8

# グラフ化
plt.figure(figsize=(10, 6))
plt.plot(t, concentration)
plt.xlabel('Time (s)')
plt.ylabel('Concentration (mol/L)')
plt.title('Concentration vs. Time for 1st Order Reaction')
plt.grid(True)
plt.show()

このコードは、1次反応の化学反応速度を示し、反応が時間とともにどのように進行するかを予測し、それをグラフに表示します。

SciPyを使用して微分方程式を解く方法と、その結果を分かりやすくグラフ化する方法を示しました。

グラフ解説

先ほどのコードで生成されるグラフは、1次反応の化学反応速度を示しています。

以下に、そのグラフの詳細な説明をします。

X軸（横軸）：

時間（秒）を表しています。
時間は0秒から50秒の範囲でプロットされています。
これは反応が進行する時間を表しています。

Y軸（縦軸）：

濃度（$mol/L$）を表しています。
この軸は化学物質の濃度を示しており、反応が進行するにつれてどのくらい濃度が変化するかを示しています。

グラフの形状：

このグラフは指数関数的な減少を示しています。
最初の時点（$t=0$）で初濃度が$1.0 mol/L$から始まり、反応速度定数（$k=0.1 1/s$）に従って指数的に減少しています。
1次反応では、濃度は時間の経過とともに指数関数的に減少することが特徴です。

反応速度の変化：

初めは反応速度が速く、急激に濃度が減少します。
しかし、時間が経つにつれて反応速度は減少し、濃度の変化も緩やかになります。
これは1次反応の特徴で、反応物の濃度が減少するにつれて反応速度も減少します。

このグラフは、1次反応の化学反応速度が時間に対してどのように変化するかを視覚的に示しています。

初濃度から出発し、指数関数的に減少する濃度を観察することができます。

SciPyを使用して微分方程式を解くことで、化学反応の進行を数値的にモデル化し、その結果をグラフに表現することができました。

生産計画問題

経済学の問題の一例として、生産計画問題を取り上げてみましょう。

具体的には、異なる製品の生産を最適化する問題を考えます。

[条件]

• ある製造会社では、2つの異なる製品（製品Aと製品B）を生産しています。
• 各製品の生産には機械時間と原材料が必要です。
  また、売上価格と製品ごとの利益も異なります。
• 最大の利益を得るために、各製品の生産量を最適化する必要があります。

以下に、CVXPYを使用してこの問題を解くPythonコードの一部を示します：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

import cvxpy as cp

# パラメータ
# 製品Aと製品Bの一つ当たりの売上価格と利益
selling_price_A = 20
profit_A = 8
selling_price_B = 30
profit_B = 12

# 製品Aと製品Bの機械時間と原材料の要求
machine_hours_A = 2
raw_material_A = 3
machine_hours_B = 3
raw_material_B = 2

# 製品Aと製品Bの生産量を変数として設定
x_A = cp.Variable(integer=True)
x_B = cp.Variable(integer=True)

# 制約条件に非負条件を追加
constraints = [
    machine_hours_A * x_A + machine_hours_B * x_B <= 80,  # 機械時間の制約
    raw_material_A * x_A + raw_material_B * x_B <= 100,  # 原材料の制約
    x_A >= 0,  # 非負条件を追加
    x_B >= 0   # 非負条件を追加
]

# 目的関数: 利益を最大化
total_profit = selling_price_A * x_A * profit_A + selling_price_B * x_B * profit_B

# 問題を設定
problem = cp.Problem(cp.Maximize(total_profit), constraints)

# 問題を解く
problem.solve()

# 最適な生産量
optimal_production_A = x_A.value
optimal_production_B = x_B.value

# 最適な利益
optimal_profit = total_profit.value

# 結果を表示
print("最適な生産量:")
print(f"製品A: {optimal_production_A:.0f} 単位")
print(f"製品B: {optimal_production_B:.0f} 単位")
print(f"最適な利益: ${optimal_profit:.2f}")

このコードでは、製品Aと製品Bの生産を最適化し、最大の利益を得るための最適な生産量と最適な利益を求めています。

[実行結果]

1
2
3
4

最適な生産量:
製品A: 1 単位
製品B: 26 単位
最適な利益: $9520.00

ソースコード解説

以下はコードの詳細な説明です：

1. cvxpy ライブラリをインポートします。

1

import cvxpy as cp

2. 問題に関連するパラメータを定義します。

これらは、製品Aと製品Bに関する売上価格、利益、機械時間、原材料の要求などの情報です。

1
2
3
4
5
6
7
8
9
10
11

# 製品Aと製品Bの一つ当たりの売上価格と利益
selling_price_A = 20
profit_A = 8
selling_price_B = 30
profit_B = 12

# 製品Aと製品Bの機械時間と原材料の要求
machine_hours_A = 2
raw_material_A = 3
machine_hours_B = 3
raw_material_B = 2

3. 製品Aと製品Bの生産量を変数として定義します。

cp.Variable 関数を使用して、整数制約（integer=True）および非負制約（nonneg=True）を持つ変数 x_A と x_B を作成します。

1
2
3

# 製品Aと製品Bの生産量を変数として設定
x_A = cp.Variable(integer=True)
x_B = cp.Variable(integer=True)

4. 制約条件を設定します。

この場合、2つの制約があります。
1つは機械時間の制約で、もう1つは原材料の制約です。
また、製品Aと製品Bの生産量が非負であることも制約条件に含まれています。

1
2
3
4
5
6
7

# 制約条件に非負条件を追加
constraints = [
    machine_hours_A * x_A + machine_hours_B * x_B <= 80,  # 機械時間の制約
    raw_material_A * x_A + raw_material_B * x_B <= 100,  # 原材料の制約
    x_A >= 0,  # 非負条件を追加
    x_B >= 0   # 非負条件を追加
]

5. 目的関数を定義します。

この場合、最大化したい目的は総利益です。
総利益は、製品Aと製品Bの売上価格と利益から計算されます。

1
2

# 目的関数: 利益を最大化
total_profit = selling_price_A * x_A * profit_A + selling_price_B * x_B * profit_B

6. 問題を設定します。

ここでは、目的関数を最大化する問題と制約条件を指定しています。

1
2

# 問題を設定
problem = cp.Problem(cp.Maximize(total_profit), constraints)

7. 最適化問題を解きます。

problem.solve() を呼び出すことで、最適な製品Aと製品Bの生産量および最適な利益が計算されます。

1
2

# 問題を解く
problem.solve()

8. 最適な生産量と最適な利益を取得し、結果を表示します。

1
2
3
4
5
6
7
8
9
10
11
12

# 最適な生産量
optimal_production_A = x_A.value
optimal_production_B = x_B.value

# 最適な利益
optimal_profit = total_profit.value

# 結果を表示
print("最適な生産量:")
print(f"製品A: {optimal_production_A:.0f} 単位")
print(f"製品B: {optimal_production_B:.0f} 単位")
print(f"最適な利益: ${optimal_profit:.2f}")

このコードは、製品Aと製品Bの生産計画を最適化し、最適な利益を計算する完全なプロセスを示しています。

最適な生産量は整数制約を満たし、最適な利益は問題の解として計算されます。

生産と配送の最適化

特定の製品の生産と配送に関する問題を考えます。

• 3つの工場（A、B、C）と4つの顧客（1、2、3、4）があります。
• 各工場での生産コストと各顧客への配送料が異なります。
• 各工場の生産能力には制限があります。

目標は、生産と配送のコストを最小化するための最適な計画を見つけることです。

以下は、この問題をPuLPを使用して解決するPythonコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

from pulp import LpProblem, LpMinimize, LpVariable

# 工場と顧客の情報
factories = ['A', 'B', 'C']
customers = [1, 2, 3, 4]

# 生産コスト（工場ごと）
production_costs = {
    ('A', 1): 10,
    ('A', 2): 11,
    ('A', 3): 12,
    ('A', 4): 14,
    ('B', 1): 12,
    ('B', 2): 9,
    ('B', 3): 13,
    ('B', 4): 8,
    ('C', 1): 14,
    ('C', 2): 13,
    ('C', 3): 7,
    ('C', 4): 9,
}

# 配送料（工場から顧客へ）
shipping_costs = {
    ('A', 1): 4,
    ('A', 2): 6,
    ('A', 3): 8,
    ('A', 4): 10,
    ('B', 1): 6,
    ('B', 2): 5,
    ('B', 3): 7,
    ('B', 4): 8,
    ('C', 1): 9,
    ('C', 2): 7,
    ('C', 3): 4,
    ('C', 4): 5,
}

# 生産変数と配送変数を定義
production = LpVariable.dicts("Production", [(f, c) for f in factories for c in customers], lowBound=0, cat="Integer")
shipping = LpVariable.dicts("Shipping", [(f, c) for f in factories for c in customers], lowBound=0, cat="Integer")

# 最小化問題を定義
problem = LpProblem("ProductionAndShipping", LpMinimize)

# 目的関数の設定（生産と配送のコストを最小化）
problem += sum(production_costs[(f, c)] * production[(f, c)] for f in factories for c in customers) + \
           sum(shipping_costs[(f, c)] * shipping[(f, c)] for f in factories for c in customers), "Total_Cost"

# 制約条件の追加

# 各工場の生産能力制約
for f in factories:
    problem += sum(production[(f, c)] for c in customers) <= 100

# 顧客の需要制約
for c in customers:
    problem += sum(shipping[(f, c)] for f in factories) == 50

# 生産と配送の関連性
for f in factories:
    for c in customers:
        problem += production[(f, c)] <= 1000 * shipping[(f, c)]

# 問題を解く
problem.solve()

# 結果を出力
for f in factories:
    for c in customers:
        print(f"Production({f}, {c}): {production[(f, c)].varValue}")
        print(f"Shipping({f}, {c}): {shipping[(f, c)].varValue}")

print(f"Total Cost: ${problem.objective.value()}")

このコードを実行すると、各工場から各顧客への生産量と配送量が計算され、総コストが最小化された最適な計画が表示されます。

[実行結果]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Production(A, 1): 0.0
Shipping(A, 1): 50.0
Production(A, 2): 0.0
Shipping(A, 2): 0.0
Production(A, 3): 0.0
Shipping(A, 3): 0.0
Production(A, 4): 0.0
Shipping(A, 4): 0.0
Production(B, 1): 0.0
Shipping(B, 1): 0.0
Production(B, 2): 0.0
Shipping(B, 2): 50.0
Production(B, 3): 0.0
Shipping(B, 3): 0.0
Production(B, 4): 0.0
Shipping(B, 4): 0.0
Production(C, 1): 0.0
Shipping(C, 1): 0.0
Production(C, 2): 0.0
Shipping(C, 2): 0.0
Production(C, 3): 0.0
Shipping(C, 3): 50.0
Production(C, 4): 0.0
Shipping(C, 4): 50.0
Total Cost: $900.0

このように、PuLPを使用することで、複雑な最適化問題を効率的に解決し、最適な意思決定を支援することができます。

ソースコード解説

以下ではソースコードの各部分を詳しく説明します。

1. PuLPの必要なモジュールをインポートします。

1

from pulp import LpProblem, LpMinimize, LpVariable

2. 問題に関連する情報を定義します。

具体的には、工場と顧客の情報、生産コスト、配送料、変数などを設定します。

• factories: 3つの工場（A、B、C）を表すリスト。

• customers: 4つの顧客（1、2、3、4）を表すリスト。

• production_costs: 各工場と顧客の組み合わせごとに生産コストを示す辞書。例えば、('A', 1)のエントリは工場Aから顧客1への生産コストを示しています。

• shipping_costs: 各工場から顧客への配送料を示す辞書。例えば、('A', 1)のエントリは工場Aから顧客1への配送料を示しています。

3. 変数を定義します。

PuLPのLpVariableを使用して、生産量（production）と配送量（shipping）の変数を定義します。
これらの変数は、工場と顧客の組み合わせごとに設定されます。
lowBound=0は、変数が非負であることを示し、cat="Integer"は変数が整数であることを示します。

1
2

production = LpVariable.dicts("Production", [(f, c) for f in factories for c in customers], lowBound=0, cat="Integer")
shipping = LpVariable.dicts("Shipping", [(f, c) for f in factories for c in customers], lowBound=0, cat="Integer")

4. 最小化問題を定義します。

LpProblemを使用して、最小化問題を作成し、問題名を指定します（”ProductionAndShipping”）。
この問題では、生産と配送のコストを最小化することが目標です。

1

problem = LpProblem("ProductionAndShipping", LpMinimize)

5. 目的関数を設定します。

目的関数は、生産コストと配送料の合計を最小化するように設定されています。

1
2

problem += sum(production_costs[(f, c)] * production[(f, c)] for f in factories for c in customers) + \
           sum(shipping_costs[(f, c)] * shipping[(f, c)] for f in factories for c in customers), "Total_Cost"

6. 制約条件を追加します。

以下のような制約条件が設定されています：

• 各工場の生産能力制約
• 顧客の需要制約
• 生産と配送の関連性

7. 問題を解決します。

problem.solve()を呼び出すことで、PuLPによって最適な解が計算されます。

8. 最適な解を出力します。

工場ごとの生産量と配送量、および最適な総コストが表示されます。

このプログラムは、与えられた制約条件の下で最適な生産と配送計画を見つけ、最小化すべき総コストを計算するためにPuLPを使用する例です。

最適な計画は、問題に対する最適な意思決定をサポートします。

結果解説

この結果は、与えられた生産および配送問題に対するPuLPの最適な計画を示しています。

[実行結果]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Production(A, 1): 0.0
Shipping(A, 1): 50.0
Production(A, 2): 0.0
Shipping(A, 2): 0.0
Production(A, 3): 0.0
Shipping(A, 3): 0.0
Production(A, 4): 0.0
Shipping(A, 4): 0.0
Production(B, 1): 0.0
Shipping(B, 1): 0.0
Production(B, 2): 0.0
Shipping(B, 2): 50.0
Production(B, 3): 0.0
Shipping(B, 3): 0.0
Production(B, 4): 0.0
Shipping(B, 4): 0.0
Production(C, 1): 0.0
Shipping(C, 1): 0.0
Production(C, 2): 0.0
Shipping(C, 2): 0.0
Production(C, 3): 0.0
Shipping(C, 3): 50.0
Production(C, 4): 0.0
Shipping(C, 4): 50.0
Total Cost: $900.0

結果を以下に詳しく説明します。

• Production(A, 1): 0.0 〜 Production(C, 4): 0.0:
  各工場（A、B、C）での各顧客（1、2、3、4）への製品の生産量です。
  この結果では、すべての工場での製品生産量が0であることを示しています。
  つまり、工場での実際の製品の生産は行われていません。

• Shipping(A, 1): 50.0 〜 Shipping(C, 4): 50.0:
  各工場から各顧客への製品の配送量です。
  この結果では、各工場（A、B、C）が各顧客（1、2、3、4）に対して50単位の製品を配送することが示されています。
  つまり、工場から顧客への配送が行われ、各顧客への需要が満たされています。

• Total Cost: $900.0:
  この問題の最適化目標は、生産と配送のコストを最小化することであり、最適な計画に基づいて計算された総コストです。
  この場合、総コストは900ドルです。

結果から分かるように、最適な計画では工場での製品生産は行わず、すべての需要を顧客への製品の配送によって満たしています。

各工場が顧客への配送を担当し、最小の総コストで製品を供給しています。

テキスト分類問題

scikit-learnを使用してテキスト分類問題を解決します。

ここでは、映画レビューのテキストを肯定的なレビューと否定的なレビューに分類する問題を解決します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
from sklearn.metrics import accuracy_score, confusion_matrix
import nltk
from nltk.corpus import movie_reviews

# 映画レビューデータセットを読み込む
nltk.download('movie_reviews')
reviews = [movie_reviews.raw(fileid) for fileid in movie_reviews.fileids()]

# レビューの肯定的/否定的なラベルを作成
labels = [1 if fileid.split('/')[0] == 'pos' else 0 for fileid in movie_reviews.fileids()]

# TF-IDFベクトル化を使用してテキストデータを数値データに変換
tfidf_vectorizer = TfidfVectorizer(max_features=5000)
X = tfidf_vectorizer.fit_transform(reviews)

# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=0.3, random_state=42)

# サポートベクトルマシン（SVM）を使った分類器を訓練
clf = LinearSVC()
clf.fit(X_train, y_train)

# テストデータで予測
y_pred = clf.predict(X_test)

# 精度を計算
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

このコードでは、映画レビューのテキストをTF-IDFベクトル化して、サポートベクトルマシン（SVM）を使用して肯定的なレビューと否定的なレビューに分類しています。

精度を計算してモデルの性能を評価します。

[実行結果]

1
2
3

[nltk_data] Downloading package movie_reviews to /root/nltk_data...
[nltk_data]   Unzipping corpora/movie_reviews.zip.
Accuracy: 0.8183333333333334

Accuracyが0.8183であることから、このモデルは比較的高い精度を持っていると言えます。

ソースコード解説

このソースコードは、映画レビューのテキストデータを分類するために、サポートベクトルマシン（SVM）を使用する機械学習モデルを構築します。

以下では、各部分を詳細に説明します。

1. ライブラリのインポート:

   • numpy: 数値計算用のPythonライブラリ。
   • matplotlib.pyplot: データの可視化のためのライブラリ。
   • TfidfVectorizer: テキストデータを数値データに変換するためのTF-IDFベクトル化を提供するscikit-learnのクラス。
   • train_test_split: データセットをトレーニングセットとテストセットに分割するための関数。
   • LinearSVC: 線形サポートベクトルマシン（SVM）分類器を提供するscikit-learnのクラス。
   • accuracy_score: 分類の精度を計算するための関数。
   • confusion_matrix: 混同行列（分類の評価指標の一部）を計算するための関数。
   • nltk: Natural Language Toolkit（自然言語処理のライブラリ）。
   • movie_reviews: NLTKに含まれる映画レビューのコーパス。

2. 映画レビューデータセットの読み込み:

   • nltk.download('movie_reviews'): NLTKから映画レビューデータセットをダウンロードするためのコマンド。
   • reviews: 映画レビューのテキストを格納するリストを作成します。

3. レビューの肯定的/否定的なラベルの作成:

   • labels: レビューテキストのファイルIDから肯定的（’pos’）または否定的（’neg’）なラベルを作成するためのリスト。
     このデータセットでは、フォルダ構造を利用してラベルを決定しています。

4. TF-IDFベクトル化:

   • TfidfVectorizer: テキストデータをTF-IDF（Term Frequency-Inverse Document Frequency）ベクトル化するためのオブジェクトを作成します。
     TF-IDFは、テキスト内の単語の重要性を示すための方法で、各単語をベクトルで表現します。
   • max_features=5000: ベクトルの次元数を制限し、最も頻出の単語トークンのみを選択します。

5. データのトレーニングセットとテストセットへの分割:

   • train_test_split: データセットをトレーニングセットとテストセットに分割します。
     test_size=0.3は、テストセットの割合を設定しています。

6. サポートベクトルマシン（SVM）モデルのトレーニング:

   • LinearSVC(): 線形SVM分類器のインスタンスを作成します。
   • fit(): トレーニングデータを使用してモデルをトレーニングします。

7. テストデータでの予測:

   • predict(): テストデータを使用してクラスの予測を行います。

8. 精度の計算:

   • accuracy_score(): テストデータに対する予測の精度を計算します。

9. 精度の表示:

   • print("Accuracy:", accuracy): 精度をコンソールに表示します。

このコードは、テキストデータの前処理、機械学習モデルのトレーニング、評価をすべて含んでおり、映画レビューの肯定的/否定的な分類タスクを解決するための完全なワークフローを提供しています。

生産量最適化

ある製造会社が3つの製品を生産しており、それぞれの製品の生産量と利益が与えられています。

また、製造には制約条件があり、生産量の合計や資源の制約を考慮する必要があります。

以下のようなデータが与えられたとします：

• 製品1の生産量: 100個、利益: 10ドル/個
• 製品2の生産量: 200個、利益: 15ドル/個
• 製品3の生産量: 150個、利益: 12ドル/個

また、以下の制約条件があります：

• 製品1の生産量は最大200個まで
• 製品2の生産量は最大300個まで
• 製品3の生産量は最大250個まで
• 資源の制約により、生産量の合計は最大500個まで

この問題をCVXPYを使って解いてみましょう。以下はPythonのコード例です：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import cvxpy as cp

# 変数の定義
x1 = cp.Variable(integer=True)
x2 = cp.Variable(integer=True)
x3 = cp.Variable(integer=True)

# 制約条件の定義
constraints = [
    x1 >= 0,
    x2 >= 0,
    x3 >= 0,
    x1 <= 200,
    x2 <= 300,
    x3 <= 250,
    x1 + x2 + x3 <= 500
]

# 目的関数の定義
objective = cp.Maximize(10*x1 + 15*x2 + 12*x3)

# 最適化問題の定義
problem = cp.Problem(objective, constraints)

# 問題の解決
result = problem.solve()

# 結果の表示
print("最適な生産量:")
print("製品1:", x1.value)
print("製品2:", x2.value)
print("製品3:", x3.value)
print("最大利益:", result)

このコードを実行すると、最適な生産量と最大利益が表示されます。

[実行結果]

1
2
3
4
5

最適な生産量:
製品1: 0.0
製品2: 300.0
製品3: 200.0
最大利益: 6900.0

ソースコード解説

以下はコードの各部分の詳細です。

1. import cvxpy as cp:

CVXPYをインポートしています。
CVXPYは凸最適化問題を解決するためのPythonライブラリです。

2. 変数の定義:

x1、x2、x3はそれぞれ製品1、製品2、製品3の生産量を表す整数変数です。
整数変数として定義されているため、これらの変数は整数値しか取ることができません。

3. 制約条件の定義:

constraintsリストには、製品の生産量に関する制約条件が含まれています。
これらの制約条件は次の通りです。

• x1 >= 0: 製品1の生産量は0以上である必要があります。
• x2 >= 0: 製品2の生産量は0以上である必要があります。
• x3 >= 0: 製品3の生産量は0以上である必要があります。
• x1 <= 200: 製品1の生産量は最大で200である必要があります。
• x2 <= 300: 製品2の生産量は最大で300である必要があります。
• x3 <= 250: 製品3の生産量は最大で250である必要があります。
• x1 + x2 + x3 <= 500: 生産総量は500以下である必要があります。

4. 目的関数の定義:

objectiveは最大化したい目的関数です。
この場合、最大化したいのは総利益であり、それは 10*x1 + 15*x2 + 12*x3 という式で表されています。
製品ごとの単価（10、15、12）と生産量の積の総和を最大化します。

5. 最適化問題の定義:

problemは最適化問題を定義するために使用されます。
目的関数と制約条件がこの問題に含まれています。

6. 問題の解決:

result = problem.solve()で最適化問題が解かれ、最適解が計算されます。
最適解は最大利益を示します。

7. 結果の表示:

最適な生産量と最大利益が表示されます。
x1.value、x2.value、x3.valueには最適な製品の生産量が格納され、resultには最大利益が格納されます。

このコードは、制約条件を満たしながら最大の利益を達成するために製品の生産量を最適化する方法を示しています。