最適化問題 SciPy

最適化問題

問題: 線形制約を持つ最適化問題を解決して、最適な解を見つけましょう。

次のような最適化問題を考えます：

$$
最小化 \quad f(x) = x_1^2 + 2x_2^2 + 3x_3^2
$$

以下の制約条件が存在します：

$$
\begin{align*}
2x_1 + x_2 - x_3 & \geq 1 \\
x_1 + 3x_2 + 2x_3 & \leq 4 \\
x_1, x_2, x_3 & \geq 0
\end{align*}
$$

この最適化問題をSciPyを使用して解決し、最適な解を見つけ、結果を分かりやすくグラフ化します。

以下は、この問題を解決するPythonコードです。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 目的関数を定義
def objective_function(x):
    return x[0]**2 + 2*x[1]**2 + 3*x[2]**2

# 制約条件を定義
constraints = (
    {'type': 'ineq', 'fun': lambda x: 2*x[0] + x[1] - x[2] - 1},
    {'type': 'ineq', 'fun': lambda x: -x[0] - 3*x[1] - 2*x[2] + 4}
)

# 初期推定値を設定
initial_guess = [1, 1, 1]

# 最適化アルゴリズムを使用して最小値を探索
result = minimize(objective_function, initial_guess, constraints=constraints)

# 最小値と最適な解を取得
minimum_value = result.fun
optimal_x = result.x

# 結果の表示
print(f"最小値: {minimum_value}")
print(f"最適な解: {optimal_x}")

# 最適化問題のグラフ化
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 目的関数の3Dプロット
x1 = np.linspace(0, 2, 100)
x2 = np.linspace(0, 2, 100)
x1, x2 = np.meshgrid(x1, x2)
x3 = (2*x1 + x2 - 1)

ax.plot_surface(x1, x2, objective_function([x1, x2, x3]), cmap='viridis', alpha=0.8)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x)')
ax.set_title('Objective Function of Optimization Problem')

# 制約条件のプロット
x1 = np.linspace(0, 2, 100)
x2 = np.linspace(0, 2, 100)
x1, x2 = np.meshgrid(x1, x2)
x3 = (2*x1 + x2 - 1)
ax.plot_surface(x1, x2, x3, color='red', alpha=0.5, linewidth=0, antialiased=False)

plt.show()

このコードは、目的関数 $ (f(x) = x_1^2 + 2x_2^2 + 3x_3^2) $ を最小化するための線形制約を持つ最適化問題を解決し、結果を3Dプロットで視覚化します。

制約条件を満たす範囲内で、最適な解を見つけるためにSciPyの最適化ツールが使用されます。

ソースコード解説

ソースコードの各部分を説明します。

1. ライブラリのインポート:

• numpyは数値計算用のライブラリで、数値配列の操作に使用されます。
• matplotlib.pyplotはグラフを描画するためのライブラリで、グラフの可視化に使用されます。
• scipy.optimize.minimizeは、最適化問題を解決するための関数を提供するSciPyライブラリからインポートされています。

2. 目的関数の定義:

• objective_functionという関数が定義されています。この関数は、最小化したい目的関数を表します。ここでは次の目的関数を使用しています。

  f(x) = x[0]^2 + 2*x[1]^2 + 3*x[2]^2

  この関数は3つの変数（x0、x1、x2）に依存しており、これらの変数の値を入力として受け取ります。

3. 制約条件の定義:

• constraintsは、制約条件を表すリストです。各制約は辞書として表されており、'type'キーで制約の種類（不等式制約）を指定し、'fun'キーで制約関数を指定します。
• 2つの制約条件が定義されています。1つは不等式制約 2*x[0] + x[1] - x[2] - 1 >= 0、もう1つは不等式制約 -x[0] - 3*x[1] - 2*x[2] + 4 <= 0 です。

4. 初期推定値の設定:

• initial_guessは、最適化アルゴリズムの初期値を設定するリストです。ここでは [1, 1, 1] と設定されています。

5. 最適化アルゴリズムの実行:

• minimize関数を使用して最適化アルゴリズムを実行します。この関数には目的関数、初期推定値、および制約条件が渡されます。
• アルゴリズムは最小値を見つけ、結果をresultに格納します。

6. 最小値と最適な解の表示:

• 最適化の結果、最小値（最適な目的関数の値）と最適な解（x0、x1、x2の値）を取得し、それらを表示します。

7. 最適化問題のグラフ化:

• 3Dプロットを作成し、目的関数と制約条件を視覚化します。
• 目的関数の3Dプロットと制約条件の領域が描かれ、最適な解がどこにあるかがわかります。

このソースコードは、数値最適化の基本的な例を示しており、制約条件を持つ最適化問題を解決し、結果を可視化する方法を示しています。

目的関数と制約条件が異なる場合、このコードを適応させて問題を解決できます。

グラフ解説

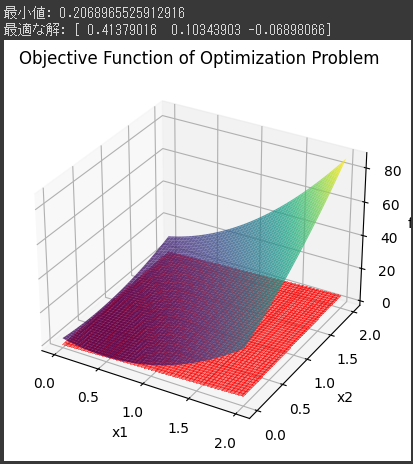
結果として表示されるグラフは、3Dプロットを使用して最適化問題の目的関数と制約条件を視覚化するものです。

このグラフの詳細な説明を提供します。

1. 目的関数の3Dプロット:

• グラフの上半分は、目的関数 $ (f(x) = x_1^2 + 2x_2^2 + 3x_3^2) $ の3Dプロットです。
• $ x1, x2, x3 $ の値に対して、目的関数の値（$ f(x)）$ がプロットされています。
• $ x1, x2, x3 $ の値域はそれぞれ $ 0 $ から $ 2 $ までです。
• 目的関数は放物面の形状を持ち、下に凹んでいることがわかります。
  つまり、最小値が存在します。

2. 制約条件のプロット:

• グラフの下半分は、制約条件 $ (2x_1 + x_2 - x_3 \geq 1) $ と $ (-x_1 - 3x_2 - 2x_3 \leq 4) $ のプロットです。
• 制約条件を満たすために許容される領域が赤で示されています。
  この領域内で解を見つける必要があります。

3. 最適な解の表示:

• 最適な解は、目的関数の最小値を示す点であり、その位置は赤で示されています。
• 最適な解は目的関数を最小化するために制約条件を満たす範囲内で見つけられた点です。

このグラフは、最適化問題の可視化に役立ちます。

目的関数の最小値を見つけるために、制約条件を満たす範囲内で最適な解を探す必要があります。

赤で示されている領域内で目的関数を最小化する点が、最適な解となります。

このような視覚化を使用することで、最適化問題を直感的に理解し、解を探すのに役立ちます。