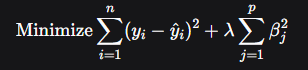1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
| import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)
class ManufacturingStation:
"""
Represents a single manufacturing station with processing time, failure rate, and capacity
"""
def __init__(self, name, mean_process_time, std_process_time, failure_rate=0.0, capacity=1):
self.name = name
self.mean_process_time = mean_process_time
self.std_process_time = std_process_time
self.failure_rate = failure_rate
self.capacity = capacity
self.queue = []
self.total_processed = 0
self.total_failed = 0
self.utilization_data = []
self.queue_length_data = []
self.processing_times = []
def get_processing_time(self):
"""Generate processing time using normal distribution with lower bound"""
time = max(0.1, np.random.normal(self.mean_process_time, self.std_process_time))
return time
def process_item(self, current_time):
"""Process an item and return success/failure status"""
process_time = self.get_processing_time()
self.processing_times.append(process_time)
if np.random.random() < self.failure_rate:
self.total_failed += 1
return False, process_time
else:
self.total_processed += 1
return True, process_time
def add_to_queue(self, item):
"""Add item to station queue"""
self.queue.append(item)
def get_queue_length(self):
"""Return current queue length"""
return len(self.queue)
class ManufacturingLine:
"""
Represents the entire manufacturing line with multiple stations
"""
def __init__(self, stations):
self.stations = stations
self.completed_products = 0
self.total_cycle_time = 0
self.cycle_times = []
self.throughput_data = []
self.bottleneck_data = []
def simulate(self, simulation_time=1000, arrival_rate=0.5):
"""
Run the manufacturing line simulation
Parameters:
- simulation_time: Total simulation time in minutes
- arrival_rate: Rate of new product arrivals (products per minute)
"""
current_time = 0
next_arrival = np.random.exponential(1/arrival_rate)
items_in_system = []
item_id = 0
print(f"Starting simulation for {simulation_time} minutes...")
print(f"Arrival rate: {arrival_rate} products/minute")
print("-" * 50)
while current_time < simulation_time:
if current_time >= next_arrival:
item_id += 1
items_in_system.append({
'id': item_id,
'arrival_time': current_time,
'current_station': 0,
'start_process_time': current_time,
'station_entry_times': [current_time]
})
next_arrival = current_time + np.random.exponential(1/arrival_rate)
for station_idx, station in enumerate(self.stations):
items_to_process = [item for item in items_in_system
if item['current_station'] == station_idx]
station.queue_length_data.append(len(items_to_process))
processed_items = []
for item in items_to_process[:station.capacity]:
if current_time >= item['start_process_time']:
success, process_time = station.process_item(current_time)
if success:
if station_idx < len(self.stations) - 1:
item['current_station'] += 1
item['start_process_time'] = current_time + process_time
item['station_entry_times'].append(current_time + process_time)
else:
cycle_time = current_time + process_time - item['arrival_time']
self.cycle_times.append(cycle_time)
self.completed_products += 1
processed_items.append(item)
else:
processed_items.append(item)
for item in processed_items:
if item in items_in_system:
items_in_system.remove(item)
if int(current_time) % 10 == 0:
current_throughput = self.completed_products / max(current_time, 1) * 60
self.throughput_data.append({
'time': current_time,
'throughput': current_throughput,
'items_in_system': len(items_in_system)
})
utilizations = []
for station in self.stations:
if len(station.processing_times) > 0:
avg_process_time = np.mean(station.processing_times)
utilization = min(1.0, arrival_rate * avg_process_time)
utilizations.append(utilization)
station.utilization_data.append(utilization)
else:
utilizations.append(0)
station.utilization_data.append(0)
if len(utilizations) > 0:
bottleneck_idx = np.argmax(utilizations)
self.bottleneck_data.append({
'time': current_time,
'bottleneck_station': bottleneck_idx,
'bottleneck_utilization': utilizations[bottleneck_idx]
})
current_time += 0.1
if len(self.cycle_times) > 0:
self.total_cycle_time = np.mean(self.cycle_times)
print(f"Simulation completed!")
print(f"Total products completed: {self.completed_products}")
print(f"Average cycle time: {self.total_cycle_time:.2f} minutes")
print(f"Final throughput: {self.completed_products/simulation_time*60:.2f} products/hour")
stations = [
ManufacturingStation("Component Prep", mean_process_time=3.0, std_process_time=0.5, failure_rate=0.02),
ManufacturingStation("PCB Assembly", mean_process_time=8.0, std_process_time=1.2, failure_rate=0.05),
ManufacturingStation("Screen Installation", mean_process_time=5.0, std_process_time=0.8, failure_rate=0.03),
ManufacturingStation("Quality Control", mean_process_time=6.0, std_process_time=1.0, failure_rate=0.01),
ManufacturingStation("Final Packaging", mean_process_time=2.0, std_process_time=0.3, failure_rate=0.01)
]
manufacturing_line = ManufacturingLine(stations)
manufacturing_line.simulate(simulation_time=1000, arrival_rate=0.4)
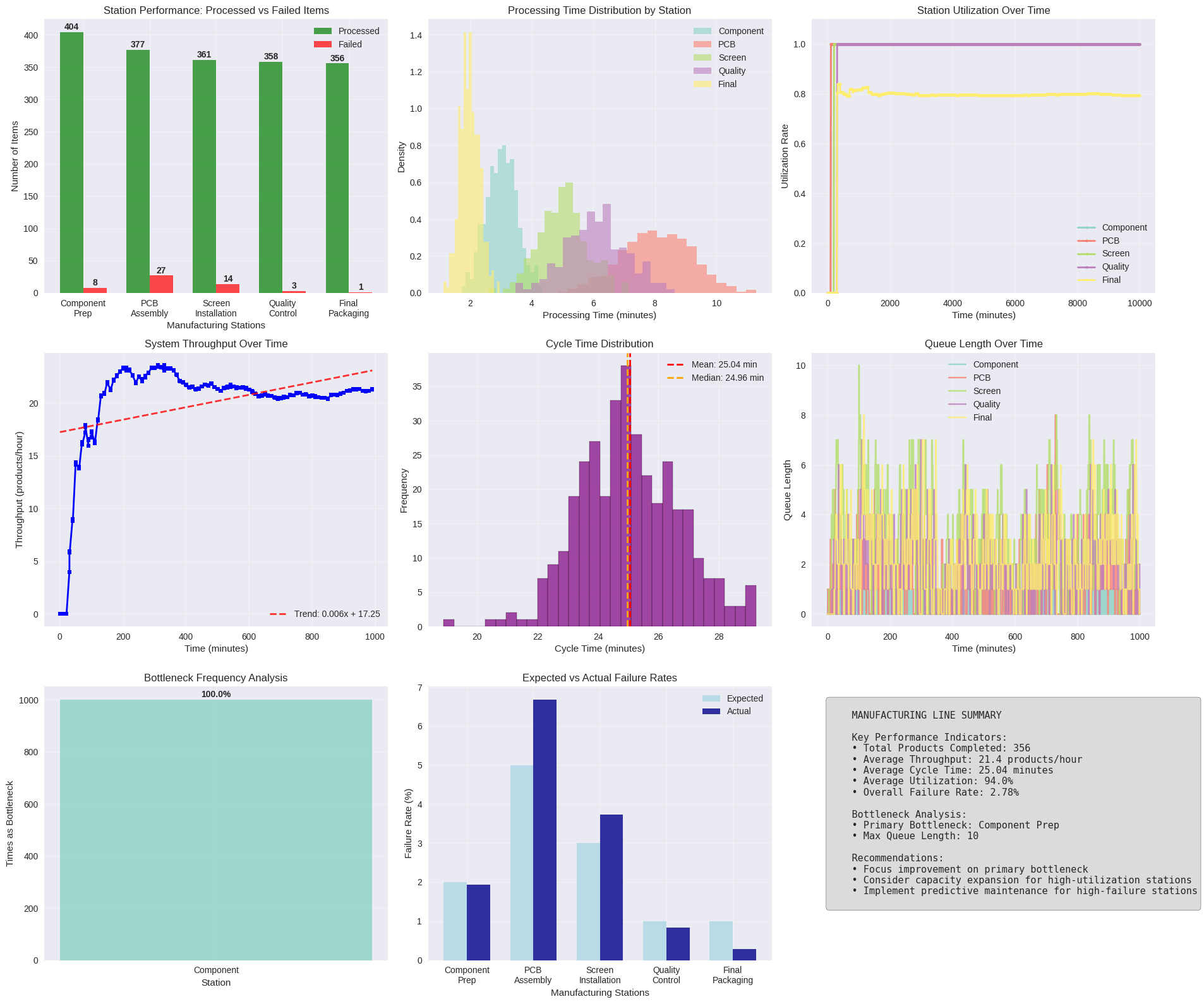
def analyze_and_visualize_results(line, stations):
"""
Comprehensive analysis and visualization of simulation results
"""
plt.style.use('seaborn-v0_8')
fig = plt.figure(figsize=(20, 16))
ax1 = plt.subplot(3, 3, 1)
station_names = [station.name for station in stations]
total_processed = [station.total_processed for station in stations]
total_failed = [station.total_failed for station in stations]
x_pos = np.arange(len(station_names))
width = 0.35
bars1 = ax1.bar(x_pos - width/2, total_processed, width, label='Processed', color='green', alpha=0.7)
bars2 = ax1.bar(x_pos + width/2, total_failed, width, label='Failed', color='red', alpha=0.7)
ax1.set_xlabel('Manufacturing Stations')
ax1.set_ylabel('Number of Items')
ax1.set_title('Station Performance: Processed vs Failed Items')
ax1.set_xticks(x_pos)
ax1.set_xticklabels([name.replace(' ', '\n') for name in station_names], rotation=0)
ax1.legend()
ax1.grid(True, alpha=0.3)
for bar in bars1:
height = bar.get_height()
ax1.text(bar.get_x() + bar.get_width()/2., height + 0.5,
f'{int(height)}', ha='center', va='bottom', fontweight='bold')
for bar in bars2:
height = bar.get_height()
if height > 0:
ax1.text(bar.get_x() + bar.get_width()/2., height + 0.5,
f'{int(height)}', ha='center', va='bottom', fontweight='bold')
ax2 = plt.subplot(3, 3, 2)
colors = plt.cm.Set3(np.linspace(0, 1, len(stations)))
for i, station in enumerate(stations):
if len(station.processing_times) > 0:
ax2.hist(station.processing_times, bins=20, alpha=0.6,
label=station.name.split()[0], color=colors[i], density=True)
ax2.set_xlabel('Processing Time (minutes)')
ax2.set_ylabel('Density')
ax2.set_title('Processing Time Distribution by Station')
ax2.legend()
ax2.grid(True, alpha=0.3)
ax3 = plt.subplot(3, 3, 3)
time_points = np.arange(0, len(stations[0].utilization_data)) * 10
for i, station in enumerate(stations):
if len(station.utilization_data) > 0:
ax3.plot(time_points[:len(station.utilization_data)],
station.utilization_data,
label=station.name.split()[0],
color=colors[i],
linewidth=2,
marker='o',
markersize=3)
ax3.set_xlabel('Time (minutes)')
ax3.set_ylabel('Utilization Rate')
ax3.set_title('Station Utilization Over Time')
ax3.legend()
ax3.grid(True, alpha=0.3)
ax3.set_ylim(0, 1.1)
ax4 = plt.subplot(3, 3, 4)
throughput_df = pd.DataFrame(line.throughput_data)
if not throughput_df.empty:
ax4.plot(throughput_df['time'], throughput_df['throughput'],
color='blue', linewidth=2, marker='s', markersize=4)
ax4.set_xlabel('Time (minutes)')
ax4.set_ylabel('Throughput (products/hour)')
ax4.set_title('System Throughput Over Time')
ax4.grid(True, alpha=0.3)
z = np.polyfit(throughput_df['time'], throughput_df['throughput'], 1)
p = np.poly1d(z)
ax4.plot(throughput_df['time'], p(throughput_df['time']),
"r--", alpha=0.8, linewidth=2, label=f'Trend: {z[0]:.3f}x + {z[1]:.2f}')
ax4.legend()
ax5 = plt.subplot(3, 3, 5)
if len(line.cycle_times) > 0:
ax5.hist(line.cycle_times, bins=30, color='purple', alpha=0.7, edgecolor='black')
ax5.axvline(np.mean(line.cycle_times), color='red', linestyle='--',
linewidth=2, label=f'Mean: {np.mean(line.cycle_times):.2f} min')
ax5.axvline(np.median(line.cycle_times), color='orange', linestyle='--',
linewidth=2, label=f'Median: {np.median(line.cycle_times):.2f} min')
ax5.set_xlabel('Cycle Time (minutes)')
ax5.set_ylabel('Frequency')
ax5.set_title('Cycle Time Distribution')
ax5.legend()
ax5.grid(True, alpha=0.3)
ax6 = plt.subplot(3, 3, 6)
for i, station in enumerate(stations):
if len(station.queue_length_data) > 0:
time_points = np.arange(len(station.queue_length_data)) * 0.1
ax6.plot(time_points, station.queue_length_data,
label=station.name.split()[0],
color=colors[i],
alpha=0.8)
ax6.set_xlabel('Time (minutes)')
ax6.set_ylabel('Queue Length')
ax6.set_title('Queue Length Over Time')
ax6.legend()
ax6.grid(True, alpha=0.3)
ax7 = plt.subplot(3, 3, 7)
bottleneck_df = pd.DataFrame(line.bottleneck_data)
if not bottleneck_df.empty:
bottleneck_counts = bottleneck_df['bottleneck_station'].value_counts().sort_index()
station_labels = [stations[i].name.split()[0] for i in bottleneck_counts.index]
bars = ax7.bar(station_labels, bottleneck_counts.values,
color=colors[:len(bottleneck_counts)], alpha=0.8)
ax7.set_xlabel('Station')
ax7.set_ylabel('Times as Bottleneck')
ax7.set_title('Bottleneck Frequency Analysis')
ax7.grid(True, alpha=0.3)
total_observations = len(bottleneck_df)
for bar, count in zip(bars, bottleneck_counts.values):
percentage = (count / total_observations) * 100
ax7.text(bar.get_x() + bar.get_width()/2., bar.get_height() + 0.5,
f'{percentage:.1f}%', ha='center', va='bottom', fontweight='bold')
ax8 = plt.subplot(3, 3, 8)
failure_rates = []
actual_failure_rates = []
for station in stations:
failure_rates.append(station.failure_rate * 100)
total_attempts = station.total_processed + station.total_failed
if total_attempts > 0:
actual_failure_rates.append((station.total_failed / total_attempts) * 100)
else:
actual_failure_rates.append(0)
x_pos = np.arange(len(station_names))
width = 0.35
bars1 = ax8.bar(x_pos - width/2, failure_rates, width,
label='Expected', color='lightblue', alpha=0.8)
bars2 = ax8.bar(x_pos + width/2, actual_failure_rates, width,
label='Actual', color='darkblue', alpha=0.8)
ax8.set_xlabel('Manufacturing Stations')
ax8.set_ylabel('Failure Rate (%)')
ax8.set_title('Expected vs Actual Failure Rates')
ax8.set_xticks(x_pos)
ax8.set_xticklabels([name.replace(' ', '\n') for name in station_names])
ax8.legend()
ax8.grid(True, alpha=0.3)
ax9 = plt.subplot(3, 3, 9)
ax9.axis('off')
avg_utilization = np.mean([np.mean(station.utilization_data)
for station in stations if len(station.utilization_data) > 0])
total_throughput = line.completed_products / 1000 * 60
avg_cycle_time = np.mean(line.cycle_times) if len(line.cycle_times) > 0 else 0
overall_failure_rate = sum(station.total_failed for station in stations) / \
sum(station.total_processed + station.total_failed for station in stations) * 100
summary_text = f"""
MANUFACTURING LINE SUMMARY
Key Performance Indicators:
• Total Products Completed: {line.completed_products:,}
• Average Throughput: {total_throughput:.1f} products/hour
• Average Cycle Time: {avg_cycle_time:.2f} minutes
• Average Utilization: {avg_utilization:.1%}
• Overall Failure Rate: {overall_failure_rate:.2f}%
Bottleneck Analysis:
• Primary Bottleneck: {stations[bottleneck_df['bottleneck_station'].mode().iloc[0]].name if not bottleneck_df.empty else 'N/A'}
• Max Queue Length: {max([max(station.queue_length_data) if station.queue_length_data else 0 for station in stations])}
Recommendations:
• Focus improvement on primary bottleneck
• Consider capacity expansion for high-utilization stations
• Implement predictive maintenance for high-failure stations
"""
ax9.text(0.05, 0.95, summary_text, transform=ax9.transAxes, fontsize=11,
verticalalignment='top', fontfamily='monospace',
bbox=dict(boxstyle="round,pad=0.3", facecolor="lightgray", alpha=0.8))
plt.tight_layout()
plt.show()
return {
'avg_throughput': total_throughput,
'avg_cycle_time': avg_cycle_time,
'avg_utilization': avg_utilization,
'failure_rate': overall_failure_rate,
'bottleneck_station': bottleneck_df['bottleneck_station'].mode().iloc[0] if not bottleneck_df.empty else None
}
results = analyze_and_visualize_results(manufacturing_line, stations)
print("\n" + "="*80)
print("DETAILED STATION ANALYSIS")
print("="*80)
for i, station in enumerate(stations):
print(f"\nStation {i+1}: {station.name}")
print("-" * 40)
print(f"Total Processed: {station.total_processed:,}")
print(f"Total Failed: {station.total_failed:,}")
if station.total_processed + station.total_failed > 0:
actual_failure_rate = station.total_failed / (station.total_processed + station.total_failed)
print(f"Actual Failure Rate: {actual_failure_rate*100:.2f}% (Expected: {station.failure_rate*100:.2f}%)")
if len(station.processing_times) > 0:
print(f"Average Processing Time: {np.mean(station.processing_times):.2f} ± {np.std(station.processing_times):.2f} minutes")
print(f"Min/Max Processing Time: {np.min(station.processing_times):.2f} / {np.max(station.processing_times):.2f} minutes")
if len(station.utilization_data) > 0:
print(f"Average Utilization: {np.mean(station.utilization_data):.1%}")
print(f"Peak Utilization: {np.max(station.utilization_data):.1%}")
if len(station.queue_length_data) > 0:
print(f"Average Queue Length: {np.mean(station.queue_length_data):.2f}")
print(f"Maximum Queue Length: {np.max(station.queue_length_data)}")
print("\n" + "="*80)
print("IMPROVEMENT RECOMMENDATIONS")
print("="*80)
utilizations = [np.mean(station.utilization_data) if station.utilization_data else 0 for station in stations]
bottleneck_idx = np.argmax(utilizations)
bottleneck_station = stations[bottleneck_idx]
print(f"\n1. PRIMARY BOTTLENECK: {bottleneck_station.name}")
print(f" - Current utilization: {utilizations[bottleneck_idx]:.1%}")
print(f" - Recommendation: Reduce processing time or add parallel capacity")
high_failure_stations = []
for station in stations:
if station.total_processed + station.total_failed > 0:
actual_failure_rate = station.total_failed / (station.total_processed + station.total_failed)
if actual_failure_rate > 0.03:
high_failure_stations.append((station, actual_failure_rate))
if high_failure_stations:
print(f"\n2. HIGH FAILURE RATE STATIONS:")
for station, rate in high_failure_stations:
print(f" - {station.name}: {rate*100:.2f}% failure rate")
print(f" Recommendation: Implement quality improvements and preventive maintenance")
print(f"\n3. POTENTIAL IMPROVEMENTS:")
current_throughput = results['avg_throughput']
if bottleneck_station.mean_process_time > 0:
improved_throughput = current_throughput * (bottleneck_station.mean_process_time / (bottleneck_station.mean_process_time * 0.8))
print(f" - 20% bottleneck improvement: +{improved_throughput - current_throughput:.1f} products/hour ({(improved_throughput/current_throughput-1)*100:.1f}% increase)")
total_failures = sum(station.total_failed for station in stations)
if total_failures > 0:
failure_improvement = total_failures * 0.5
print(f" - 50% failure reduction: +{failure_improvement/1000*60:.1f} products/hour potential gain")
print(f"\n4. SUMMARY METRICS:")
print(f" - Current throughput: {current_throughput:.1f} products/hour")
print(f" - Average cycle time: {results['avg_cycle_time']:.2f} minutes")
print(f" - System utilization: {results['avg_utilization']:.1%}")
print(f" - Overall failure rate: {results['failure_rate']:.2f}%")
|
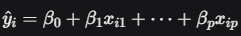 is the predicted value.
is the predicted value.