仮想通貨の価格分析
仮想通貨の分析には、価格データの取得、トレンドの分析、テクニカル指標の計算などが含まれます。
以下に、Pythonを使って簡単な仮想通貨の価格分析を行う方法を示します。
ここでは、Bitcoin(BTC)の価格データを取得し、移動平均を計算してプロットする例を紹介します。
必要なライブラリのインストール
まず、以下のライブラリをインストールしてください。
1 | pip install pandas yfinance matplotlib |
データの取得と分析
1 | import yfinance as yf |
解説
- データの取得:
yfinanceライブラリを使って、Bitcoinの過去1年間の価格データを取得します。 - 移動平均の計算:
pandasを使って、50日移動平均と200日移動平均を計算します。 - データのプロット:
matplotlibを使って、価格データと移動平均をプロットします。
この例では、Bitcoinの過去1年間の終値と、その50日および200日の移動平均を表示しています。
移動平均を使うことで、価格の長期的なトレンドを視覚的に把握することができます。
他の分析方法としては、相対力指数(RSI)、移動平均収束拡散指標(MACD)などのテクニカル指標の計算や、ボラティリティの分析なども可能です。
さらに高度な分析には、機械学習モデルを使った価格予測や、統計的手法を用いた異常検知などがあります。
[実行結果]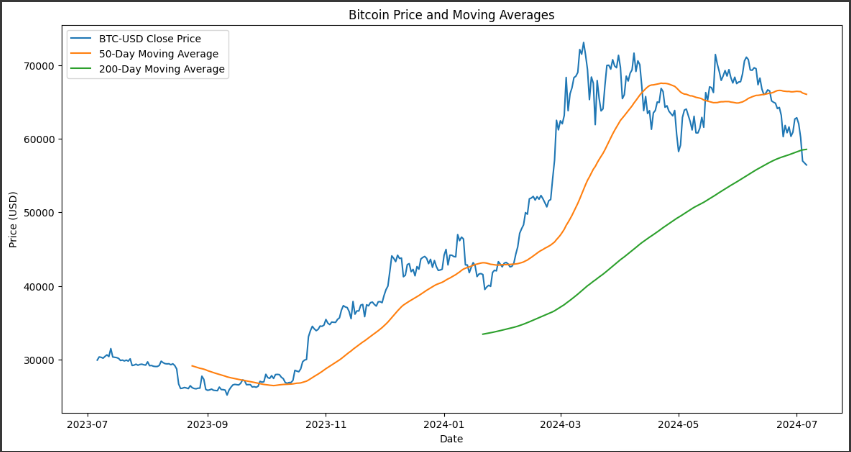
ソースコード解説
このPythonスクリプトは、Bitcoinの価格データを取得し、50日および200日移動平均を計算してプロットするものです。
以下、コードの各部分を詳しく説明します。
1. ライブラリのインポート
1 | import yfinance as yf |
この章では、必要なライブラリをインポートしています。
yfinance: Yahoo Financeから金融データを取得するためのライブラリ。pandas: データの操作や分析を行うためのライブラリ。matplotlib.pyplot: データの可視化を行うためのライブラリ。
2. データの取得
1 | btc = yf.Ticker("BTC-USD") |
この章では、Bitcoinの価格データを取得しています。
yf.Ticker("BTC-USD"):yfinanceライブラリを使用して、Bitcoin(ティッカーシンボル: BTC-USD)のデータを取得するためのオブジェクトを作成します。btc.history(period="1y"): 過去1年間のBitcoinの履歴データを取得します。このデータには、日次の価格(始値、高値、安値、終値)、取引量などが含まれます。
3. 移動平均の計算
1 | data['MA50'] = data['Close'].rolling(window=50).mean() # 50日移動平均 |
この章では、50日移動平均と200日移動平均を計算しています。
data['Close']: データフレームから終値の列を選択します。rolling(window=50): 終値の列に対して、50日間の移動ウィンドウを作成します。mean(): 移動ウィンドウ内の値の平均を計算します。この操作により、50日間の移動平均が計算されます。data['MA50']: 50日移動平均を新しい列としてデータフレームに追加します。- 同様に、
window=200として200日移動平均も計算し、data['MA200']列に追加します。
4. データのプロット
1 | plt.figure(figsize=(14, 7)) |
この章では、取得したデータと計算した移動平均をプロットしています。
plt.figure(figsize=(14, 7)): グラフのサイズを設定します。幅14インチ、高さ7インチの図を作成します。plt.plot(data['Close'], label='BTC-USD Close Price'): Bitcoinの終値をプロットし、ラベルを「BTC-USD Close Price」に設定します。plt.plot(data['MA50'], label='50-Day Moving Average'): 50日移動平均をプロットし、ラベルを「50-Day Moving Average」に設定します。plt.plot(data['MA200'], label='200-Day Moving Average'): 200日移動平均をプロットし、ラベルを「200-Day Moving Average」に設定します。plt.title('Bitcoin Price and Moving Averages'): グラフのタイトルを設定します。plt.xlabel('Date'): x軸のラベルを「Date」に設定します。plt.ylabel('Price (USD)'): y軸のラベルを「Price (USD)」に設定します。plt.legend(): 凡例を表示します。plt.show(): グラフを表示します。
これにより、Bitcoinの価格推移とその50日および200日移動平均が可視化されます。
グラフ解説
[実行結果]
このグラフは、Bitcoin(BTC-USD)の価格推移と移動平均を表示しています。
以下は、このグラフの詳細な説明です。
グラフの概要
- 期間: 過去1年間(2023年7月から2024年7月)
- データ: Bitcoinの終値(青線)
- 移動平均:
- 50日移動平均(オレンジ線)
- 200日移動平均(緑線)
詳細な説明
価格の変動(青線):
- 2023年7月から2023年11月まで: Bitcoinの価格は$30,000 $USD以下で、比較的低い水準で推移しています。
- 2023年11月から2024年3月にかけて: 大きな上昇トレンドが見られ、価格は$70,000 $USDに達しています。この期間は急激な価格上昇を示しています。
- 2024年3月以降: 価格は乱高下を繰り返しながらも、全体的に下降傾向にあります。
50日移動平均(オレンジ線):
- 短期的な価格のトレンドを示しています。価格が50日移動平均を上回っているときは上昇トレンド、下回っているときは下降トレンドと解釈されます。
- 2023年末から2024年3月にかけて上昇し、その後は価格の変動に応じて上下していますが、全体的には価格の動きに遅れて追従しています。
200日移動平均(緑線):
- 長期的な価格のトレンドを示しています。50日移動平均よりも滑らかな曲線で、価格の大きなトレンドを捉えています。
- 2023年11月から2024年7月にかけて一貫して上昇しており、価格の全体的な上昇トレンドを示しています。
結論
- 価格動向: Bitcoinの価格は2023年7月から2023年11月まで低迷していましたが、その後急激に上昇し、2024年3月にはピークに達しました。その後は価格が乱高下し、下降傾向にあります。
- 移動平均の交差: 50日移動平均が200日移動平均を上回るとゴールデンクロスと呼ばれ、強気市場のサインとされます。
一方、50日移動平均が200日移動平均を下回るとデッドクロスと呼ばれ、弱気市場のサインとされます。
グラフからは、直近でデッドクロスが発生していることが確認でき、今後の価格動向に注意が必要です。
この分析は、投資の判断材料として役立つかもしれませんが、他の要因や指標も考慮することをお勧めします。