1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
| import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings('ignore')
STEFAN_BOLTZMANN = 5.67e-8
SOLAR_CONSTANT = 1361
class SpacecraftThermalOptimizer:
"""
Spacecraft thermal design optimization considering:
- Multi-layer insulation (MLI)
- Radiative heat transfer
- Weight constraints
- Cost optimization
"""
def __init__(self):
self.surface_area = 10.0
self.electronics_power = 500
self.T_space = 4
self.T_sun_side = 393
self.T_shade_side = 173
self.T_min_electronics = 253
self.T_max_electronics = 343
self.T_min_battery = 273
self.T_max_battery = 323
self.mli_properties = {
'thermal_conductivity': 0.002,
'density': 50,
'cost_per_kg': 10000,
'emissivity_low': 0.03,
'emissivity_high': 0.8
}
self.launch_cost_per_kg = 5000
self.thermal_control_base_cost = 50000
self.penalty_cost_per_degree = 1000
def calculate_heat_transfer(self, thickness, emissivity):
"""
Calculate heat transfer through MLI and radiation
Args:
thickness: MLI thickness in meters
emissivity: Effective emissivity of outer surface
Returns:
dict: Heat transfer rates and temperatures
"""
k = self.mli_properties['thermal_conductivity']
q_conduction = (k * self.surface_area *
(self.T_sun_side - self.T_shade_side)) / thickness
T_avg_exterior = np.sqrt((self.T_sun_side**2 + self.T_shade_side**2) / 2)
q_radiation_out = (STEFAN_BOLTZMANN * self.surface_area * emissivity *
(T_avg_exterior**4 - self.T_space**4))
absorptivity = 0.3
q_solar = SOLAR_CONSTANT * self.surface_area * absorptivity * 0.5
q_net = q_solar + self.electronics_power - q_radiation_out - q_conduction
thermal_mass = 1000
T_internal = self.T_space + (q_net / (STEFAN_BOLTZMANN * self.surface_area * 0.1))
return {
'q_conduction': q_conduction,
'q_radiation_out': q_radiation_out,
'q_solar': q_solar,
'q_net': q_net,
'T_internal': T_internal,
'T_electronics': T_internal + 10,
'T_battery': T_internal + 5
}
def calculate_mass_and_cost(self, thickness):
"""Calculate MLI mass and associated costs"""
volume = self.surface_area * thickness
mass = volume * self.mli_properties['density']
launch_cost = mass * self.launch_cost_per_kg
material_cost = mass * self.mli_properties['cost_per_kg']
return mass, launch_cost + material_cost
def temperature_penalty(self, temperatures):
"""Calculate penalty for temperature violations"""
penalty = 0
T_electronics = temperatures['T_electronics']
T_battery = temperatures['T_battery']
if T_electronics < self.T_min_electronics:
penalty += (self.T_min_electronics - T_electronics) * self.penalty_cost_per_degree
elif T_electronics > self.T_max_electronics:
penalty += (T_electronics - self.T_max_electronics) * self.penalty_cost_per_degree
if T_battery < self.T_min_battery:
penalty += (self.T_min_battery - T_battery) * self.penalty_cost_per_degree
elif T_battery > self.T_max_battery:
penalty += (T_battery - self.T_max_battery) * self.penalty_cost_per_degree
return penalty
def objective_function(self, design_vars):
"""
Objective function to minimize total mission cost
Args:
design_vars: [thickness (m), emissivity]
Returns:
float: Total cost ($)
"""
thickness, emissivity = design_vars
if thickness <= 0.001 or thickness > 0.1:
return 1e10
if emissivity <= 0.01 or emissivity > 1.0:
return 1e10
heat_results = self.calculate_heat_transfer(thickness, emissivity)
mass, material_launch_cost = self.calculate_mass_and_cost(thickness)
temp_penalty = self.temperature_penalty(heat_results)
total_cost = (material_launch_cost +
self.thermal_control_base_cost +
temp_penalty)
return total_cost
def optimize_design(self):
"""Perform optimization to find optimal MLI thickness and emissivity"""
x0 = [0.02, 0.5]
bounds = [(0.001, 0.1), (0.01, 1.0)]
result = minimize(self.objective_function, x0,
method='L-BFGS-B', bounds=bounds)
return result
def analyze_design_space(self):
"""Analyze the design space to understand trade-offs"""
thickness_range = np.linspace(0.005, 0.08, 50)
emissivity_range = np.linspace(0.1, 0.9, 40)
cost_matrix = np.zeros((len(thickness_range), len(emissivity_range)))
temp_matrix = np.zeros((len(thickness_range), len(emissivity_range)))
mass_matrix = np.zeros((len(thickness_range), len(emissivity_range)))
for i, thickness in enumerate(thickness_range):
for j, emissivity in enumerate(emissivity_range):
cost = self.objective_function([thickness, emissivity])
heat_results = self.calculate_heat_transfer(thickness, emissivity)
mass, _ = self.calculate_mass_and_cost(thickness)
cost_matrix[i, j] = cost if cost < 1e9 else np.nan
temp_matrix[i, j] = heat_results['T_electronics']
mass_matrix[i, j] = mass
return thickness_range, emissivity_range, cost_matrix, temp_matrix, mass_matrix
optimizer = SpacecraftThermalOptimizer()
print("🚀 SPACECRAFT THERMAL DESIGN OPTIMIZATION")
print("=" * 50)
print("\n📊 Running optimization...")
result = optimizer.optimize_design()
optimal_thickness, optimal_emissivity = result.x
optimal_cost = result.fun
print(f"\n✅ OPTIMAL DESIGN FOUND:")
print(f" MLI Thickness: {optimal_thickness*1000:.1f} mm")
print(f" Surface Emissivity: {optimal_emissivity:.3f}")
print(f" Total Mission Cost: ${optimal_cost:,.0f}")
heat_results = optimizer.calculate_heat_transfer(optimal_thickness, optimal_emissivity)
mass, material_cost = optimizer.calculate_mass_and_cost(optimal_thickness)
print(f"\n🌡️ THERMAL PERFORMANCE:")
print(f" Electronics Temperature: {heat_results['T_electronics']:.1f} K ({heat_results['T_electronics']-273:.1f}°C)")
print(f" Battery Temperature: {heat_results['T_battery']:.1f} K ({heat_results['T_battery']-273:.1f}°C)")
print(f" Heat Conduction: {heat_results['q_conduction']:.1f} W")
print(f" Heat Radiation: {heat_results['q_radiation_out']:.1f} W")
print(f"\n⚖️ MASS AND COST BREAKDOWN:")
print(f" MLI Mass: {mass:.2f} kg")
print(f" Launch + Material Cost: ${material_cost:,.0f}")
print(f" Temperature Penalty: ${optimizer.temperature_penalty(heat_results):,.0f}")
print(f"\n🎯 DESIGN VERIFICATION:")
temp_ok = (optimizer.T_min_electronics <= heat_results['T_electronics'] <= optimizer.T_max_electronics and
optimizer.T_min_battery <= heat_results['T_battery'] <= optimizer.T_max_battery)
print(f" Temperature Constraints: {'✅ SATISFIED' if temp_ok else '❌ VIOLATED'}")
print(f"\n🔍 Analyzing design space...")
thickness_range, emissivity_range, cost_matrix, temp_matrix, mass_matrix = optimizer.analyze_design_space()
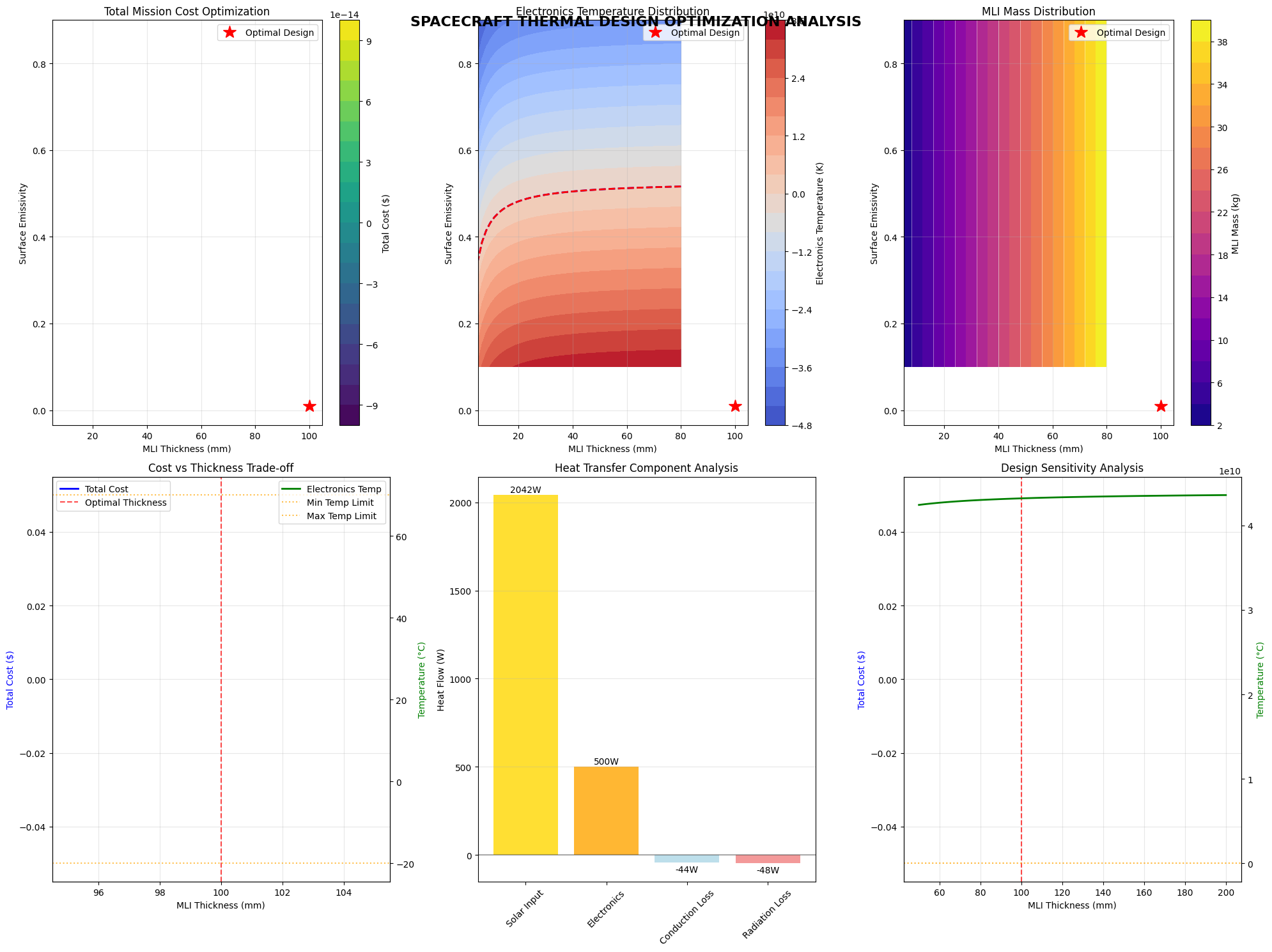
fig = plt.figure(figsize=(20, 15))
ax1 = plt.subplot(2, 3, 1)
T, E = np.meshgrid(thickness_range * 1000, emissivity_range)
valid_costs = np.where(np.isfinite(cost_matrix.T), cost_matrix.T, np.nan)
contour = plt.contourf(T, E, valid_costs, levels=20, cmap='viridis')
plt.colorbar(contour, label='Total Cost ($)')
plt.contour(T, E, valid_costs, levels=10, colors='white', alpha=0.6, linewidths=0.5)
plt.plot(optimal_thickness*1000, optimal_emissivity, 'r*', markersize=15, label='Optimal Design')
plt.xlabel('MLI Thickness (mm)')
plt.ylabel('Surface Emissivity')
plt.title('Total Mission Cost Optimization')
plt.legend()
plt.grid(True, alpha=0.3)
ax2 = plt.subplot(2, 3, 2)
temp_contour = plt.contourf(T, E, temp_matrix.T, levels=20, cmap='coolwarm')
plt.colorbar(temp_contour, label='Electronics Temperature (K)')
plt.contour(T, E, temp_matrix.T, levels=[optimizer.T_min_electronics, optimizer.T_max_electronics],
colors=['blue', 'red'], linewidths=2, linestyles=['--', '--'])
plt.plot(optimal_thickness*1000, optimal_emissivity, 'r*', markersize=15, label='Optimal Design')
plt.xlabel('MLI Thickness (mm)')
plt.ylabel('Surface Emissivity')
plt.title('Electronics Temperature Distribution')
plt.legend()
plt.grid(True, alpha=0.3)
ax3 = plt.subplot(2, 3, 3)
mass_contour = plt.contourf(T, E, mass_matrix.T, levels=20, cmap='plasma')
plt.colorbar(mass_contour, label='MLI Mass (kg)')
plt.contour(T, E, mass_matrix.T, levels=10, colors='white', alpha=0.6, linewidths=0.5)
plt.plot(optimal_thickness*1000, optimal_emissivity, 'r*', markersize=15, label='Optimal Design')
plt.xlabel('MLI Thickness (mm)')
plt.ylabel('Surface Emissivity')
plt.title('MLI Mass Distribution')
plt.legend()
plt.grid(True, alpha=0.3)
ax4 = plt.subplot(2, 3, 4)
thickness_test = np.linspace(0.005, 0.08, 100)
costs = []
temps = []
masses = []
for t in thickness_test:
cost = optimizer.objective_function([t, optimal_emissivity])
if cost < 1e9:
heat_res = optimizer.calculate_heat_transfer(t, optimal_emissivity)
mass, _ = optimizer.calculate_mass_and_cost(t)
costs.append(cost)
temps.append(heat_res['T_electronics'])
masses.append(mass)
else:
costs.append(np.nan)
temps.append(np.nan)
masses.append(np.nan)
plt.plot([t*1000 for t in thickness_test], costs, 'b-', linewidth=2, label='Total Cost')
plt.axvline(optimal_thickness*1000, color='red', linestyle='--', alpha=0.7, label='Optimal Thickness')
plt.xlabel('MLI Thickness (mm)')
plt.ylabel('Total Cost ($)', color='blue')
plt.title('Cost vs Thickness Trade-off')
plt.grid(True, alpha=0.3)
ax4_twin = ax4.twinx()
ax4_twin.plot([t*1000 for t in thickness_test], [t-273 for t in temps], 'g-', linewidth=2, label='Electronics Temp')
ax4_twin.axhline(optimizer.T_min_electronics-273, color='orange', linestyle=':', alpha=0.7, label='Min Temp Limit')
ax4_twin.axhline(optimizer.T_max_electronics-273, color='orange', linestyle=':', alpha=0.7, label='Max Temp Limit')
ax4_twin.set_ylabel('Temperature (°C)', color='green')
ax4_twin.legend(loc='upper right')
ax4.legend(loc='upper left')
ax5 = plt.subplot(2, 3, 5)
heat_components = ['Solar Input', 'Electronics', 'Conduction Loss', 'Radiation Loss']
heat_values = [heat_results['q_solar'], optimizer.electronics_power,
-heat_results['q_conduction'], -heat_results['q_radiation_out']]
colors = ['gold', 'orange', 'lightblue', 'lightcoral']
bars = plt.bar(heat_components, heat_values, color=colors, alpha=0.8)
plt.axhline(y=0, color='black', linestyle='-', alpha=0.3)
plt.ylabel('Heat Flow (W)')
plt.title('Heat Transfer Component Analysis')
plt.xticks(rotation=45)
plt.grid(True, alpha=0.3, axis='y')
for bar, value in zip(bars, heat_values):
plt.text(bar.get_x() + bar.get_width()/2, value + (5 if value > 0 else -15),
f'{value:.0f}W', ha='center', va='bottom' if value > 0 else 'top')
ax6 = plt.subplot(2, 3, 6)
thickness_sensitivity = np.linspace(optimal_thickness*0.5, optimal_thickness*2, 50)
cost_sensitivity = []
temp_sensitivity = []
for t in thickness_sensitivity:
cost = optimizer.objective_function([t, optimal_emissivity])
heat_res = optimizer.calculate_heat_transfer(t, optimal_emissivity)
cost_sensitivity.append(cost if cost < 1e9 else np.nan)
temp_sensitivity.append(heat_res['T_electronics'])
plt.plot([t*1000 for t in thickness_sensitivity], cost_sensitivity, 'b-', linewidth=2, label='Cost')
plt.axvline(optimal_thickness*1000, color='red', linestyle='--', alpha=0.7, label='Optimal')
plt.xlabel('MLI Thickness (mm)')
plt.ylabel('Total Cost ($)', color='blue')
plt.title('Design Sensitivity Analysis')
plt.grid(True, alpha=0.3)
ax6_twin = ax6.twinx()
ax6_twin.plot([t*1000 for t in thickness_sensitivity], [t-273 for t in temp_sensitivity],
'g-', linewidth=2, label='Temperature')
ax6_twin.set_ylabel('Temperature (°C)', color='green')
ax6_twin.axhline(optimizer.T_min_electronics-273, color='orange', linestyle=':', alpha=0.5)
ax6_twin.axhline(optimizer.T_max_electronics-273, color='orange', linestyle=':', alpha=0.5)
plt.tight_layout()
plt.suptitle('SPACECRAFT THERMAL DESIGN OPTIMIZATION ANALYSIS',
fontsize=16, fontweight='bold', y=0.98)
plt.show()
print(f"\n📈 DESIGN SPACE ANALYSIS:")
print(f" Design Space Explored: {len(thickness_range)} × {len(emissivity_range)} = {len(thickness_range)*len(emissivity_range)} combinations")
print(f" Feasible Designs: {np.sum(np.isfinite(cost_matrix))}")
print(f" Cost Range: ${np.nanmin(cost_matrix):,.0f} - ${np.nanmax(cost_matrix):,.0f}")
print(f" Temperature Range: {np.nanmin(temp_matrix):.1f}K - {np.nanmax(temp_matrix):.1f}K")
print(f" Mass Range: {np.nanmin(mass_matrix):.2f}kg - {np.nanmax(mass_matrix):.2f}kg")
print(f"\n🎯 OPTIMIZATION CONVERGENCE:")
print(f" Optimization Success: {'✅ YES' if result.success else '❌ NO'}")
print(f" Function Evaluations: {result.nfev}")
print(f" Final Message: {result.message}")
|