コントラクトがehterを保持していた場合、不要となったらコントラクトからetherを回収しなければなりません。

そのため、コントラクトを破棄すると同時にownerにetherを送金するようにしておく必要があります。

脆弱性が発見されることに備えて、攻撃者からの不正な引出しをされる前にetherを回収できるようにしておくことはセキュリティ的に必須です。

実装

コントラクトをきれいに破棄するためのサンプルコードは以下の通りです。

[ソースコード]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

pragma solidity ^0.4.11;
contract Mortal {
    address public owner;

    /// アクセスチェック用のmodifier
    modifier onlyOwner() {
        require(msg.sender == owner);
        _;
    }

    /// オーナーを設定
    function owned() internal {
        owner = msg.sender;
    }

    ///  オーナーを変更
    function changeOwner(address _newOwner) public onlyOwner {
        owner = _newOwner;
    }

    /// コントラクトを破棄して、etherをownerに送る
    function kill() public onlyOwner {
        selfdestruct(owner);
    }
}

contract MortalSample is Mortal{
    string public state;

    /// Fallback関数
    function() payable {
    }

    /// コンストラクタ
    function MortalSample() {
        // Ownedで定義されているowned関数をコール
        owned();

        // someStateの初期値を設定
        state = "initial";
    }
}

ポイントは23行目のselfdestruct関数です。

selfdestruct関数はコントラクトを破棄し、引数のアドレスにコントラクト内のetherを送金します。

不特定のアドレスからコントラクトを破棄されては困るので、onlyOwner(22行目)を付加して、コントラクトのオーナーからのみ実行できるようにアクセス制限をかけています。

次回は、このコントラクトの動作確認を行います。

今回は、アクセス制限を行うスマートコントラクトの動作確認を行います。

アカウントごとの役割

アカウントの役割は次の通りです。

• MAIN ACCOUNT (eth.accounts[0]) “0xec3b01f36b44182746ca109230567c4915512e35”
  コンストラクトの生成者。初期オーナー
• ACCOUNT1 (eth.accounts[1]) “0x63f25b9bbd974fdfa07477cb99c60d2073cfe560”
  ２番目のオーナー
• ACCOUNT2 (eth.accounts[2]) “0xd5adf1e9fbc1ed869ed4c7372961238fddc760a5”
  マイナー。

デプロイ

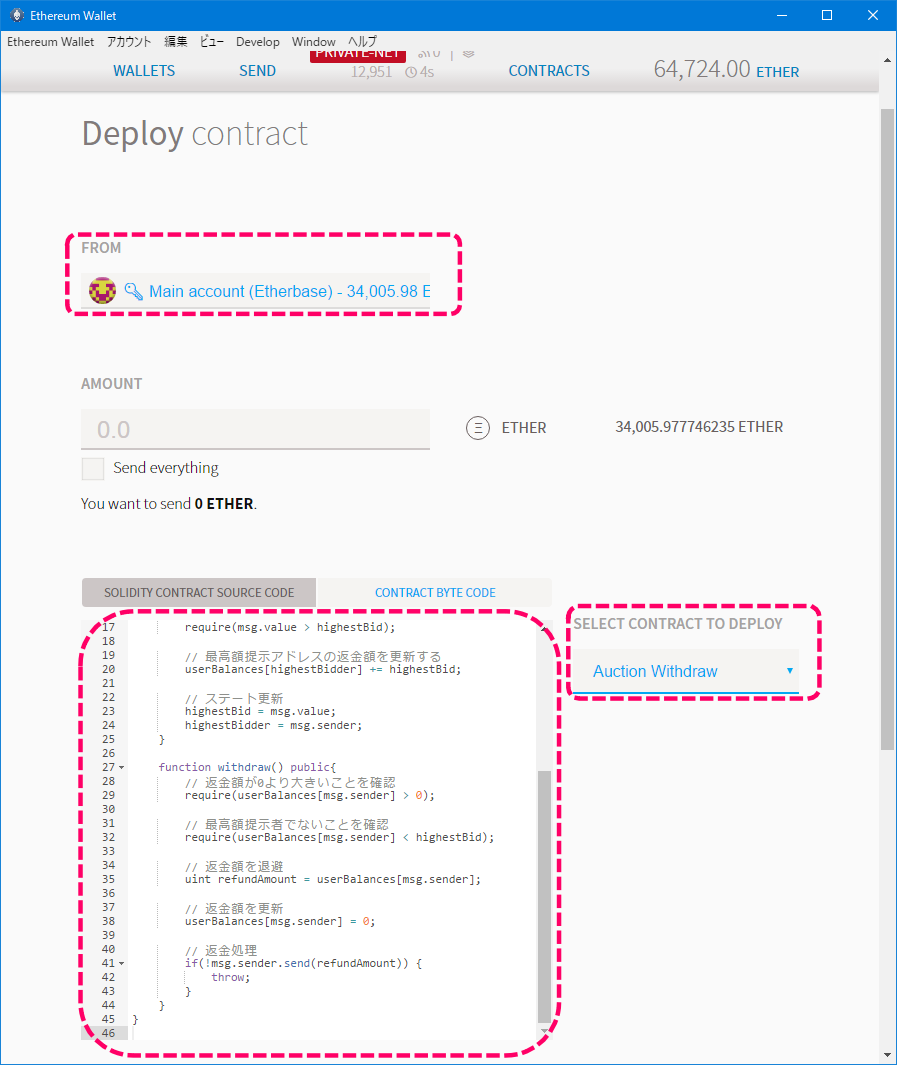
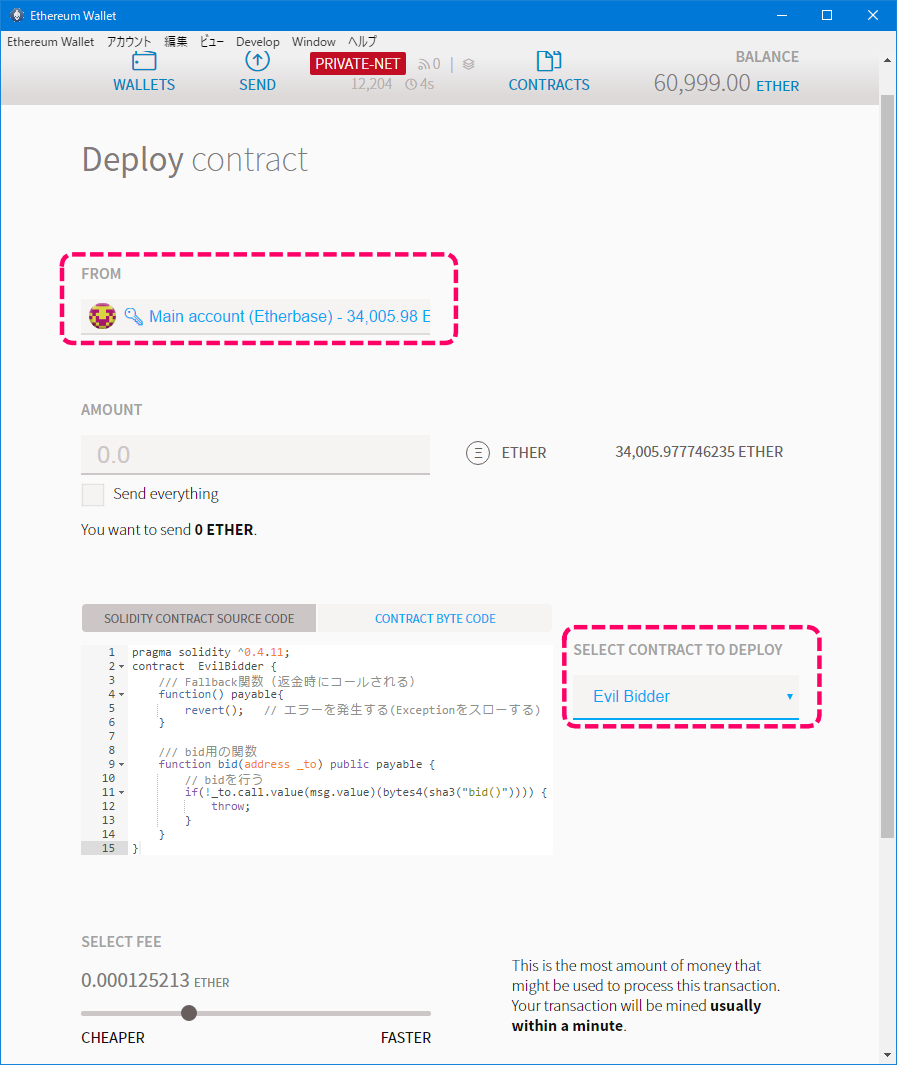
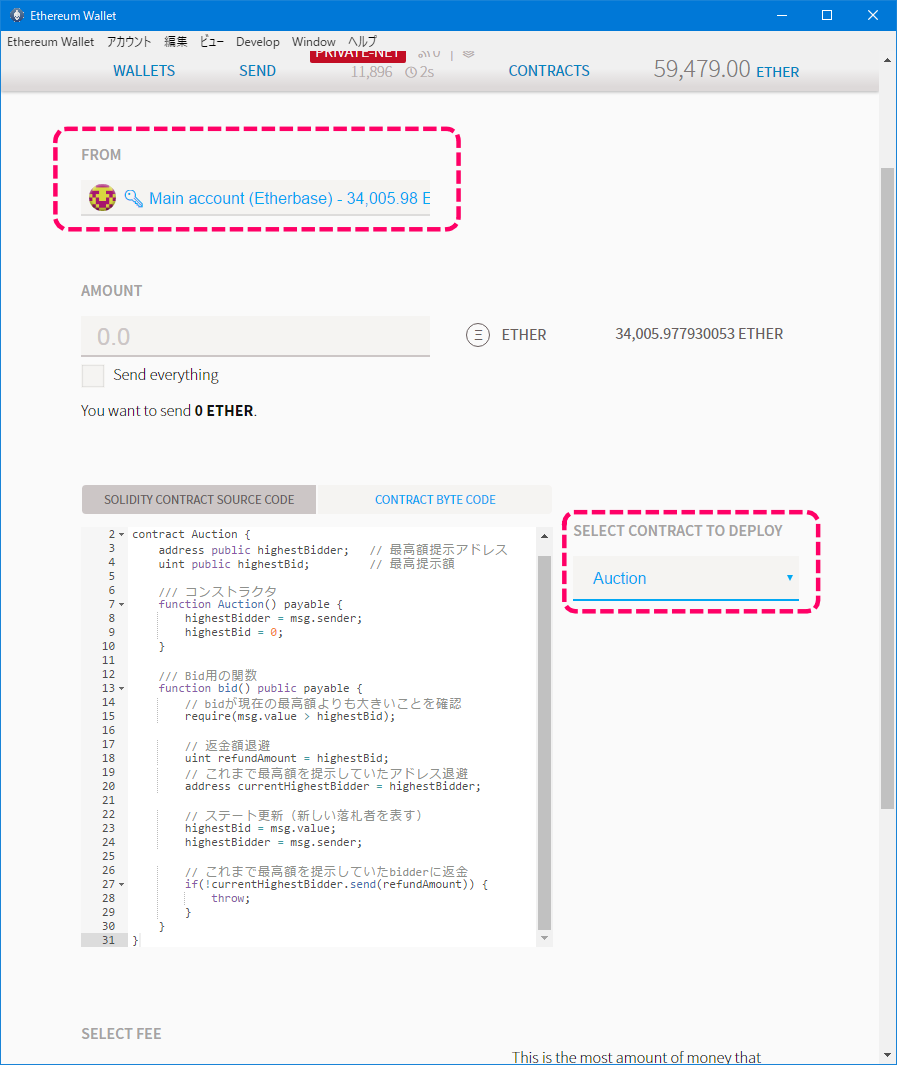
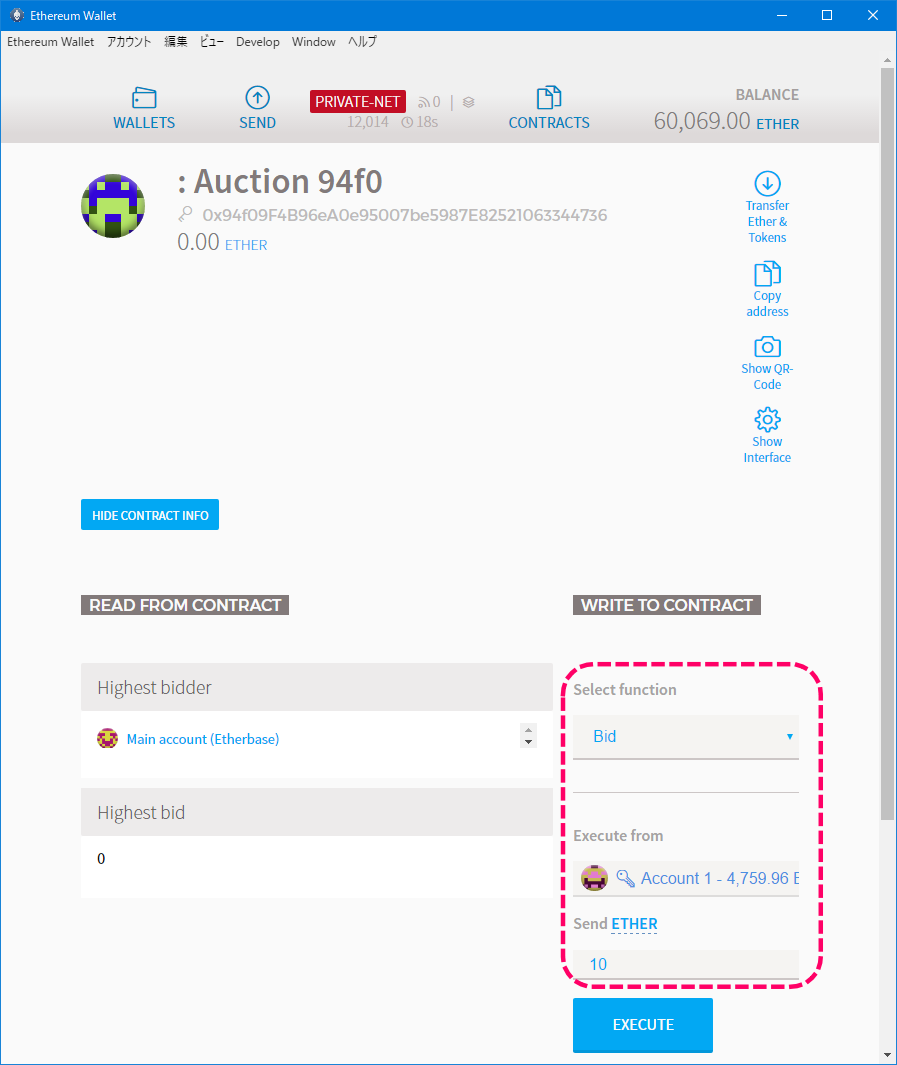
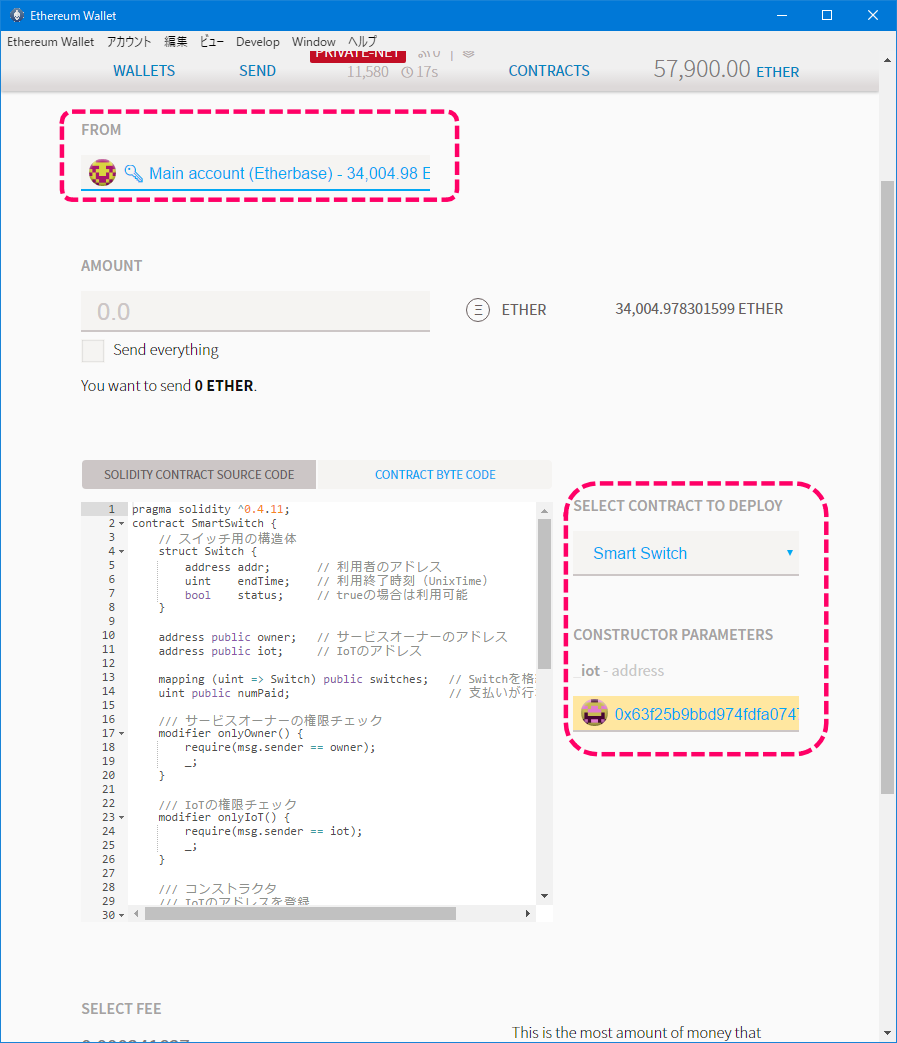
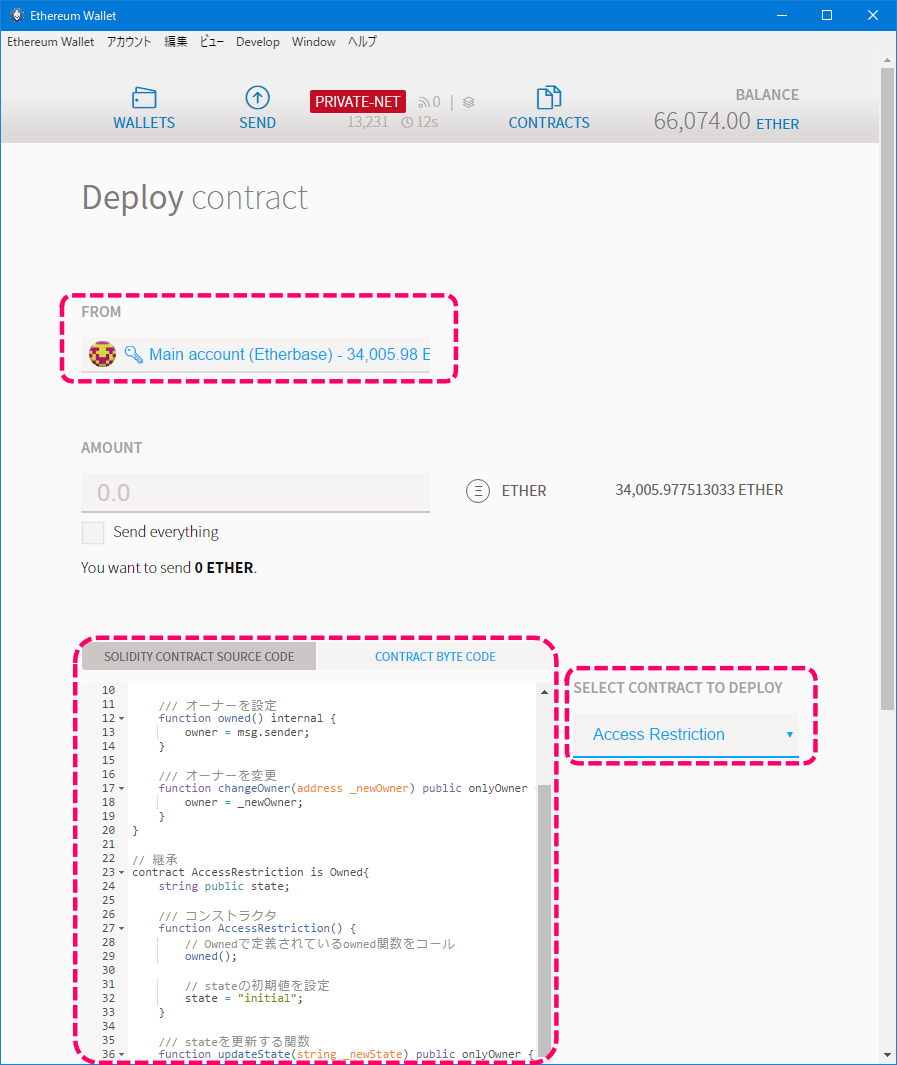
まずはデプロイを行います。デプロイアカウントはMAIN ACCOUNTです。

デプロイするコントラクトは、Ownedコントラクトを継承したAccess Restrictionコントラクトになります。

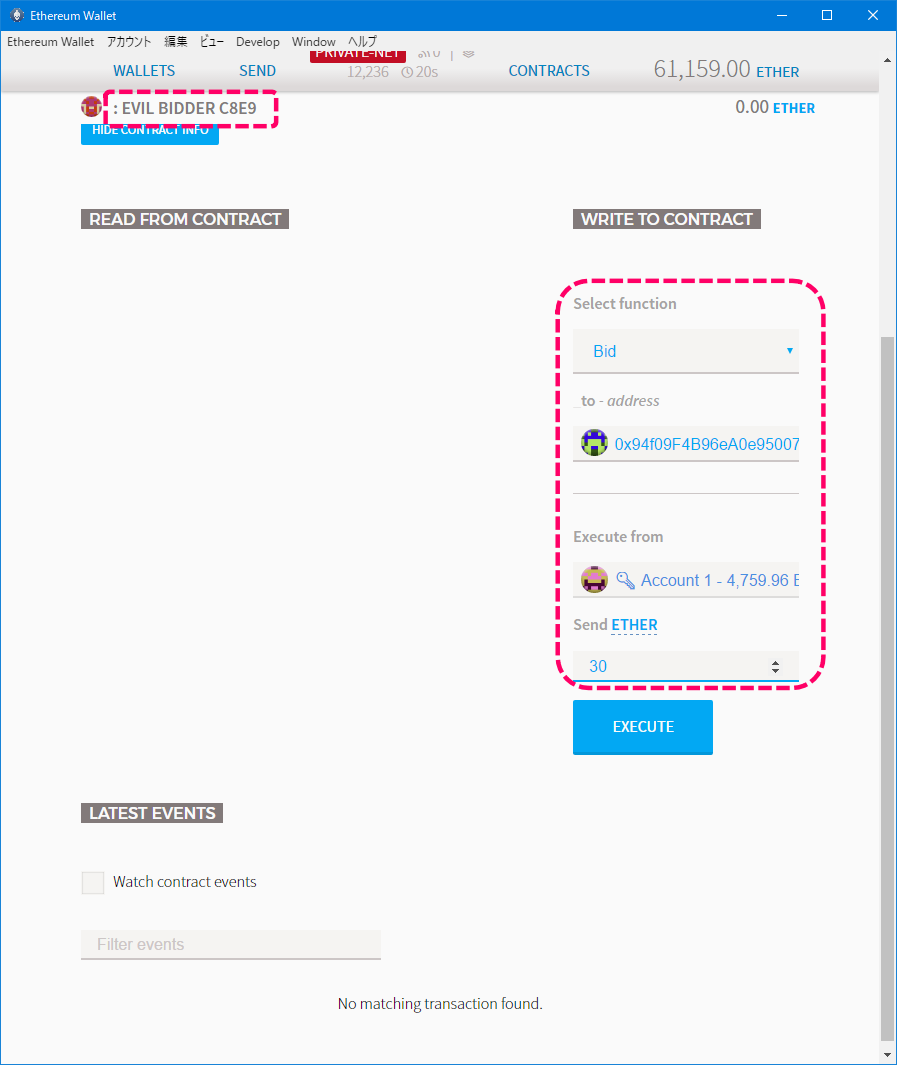
[デプロイ時のイメージ]

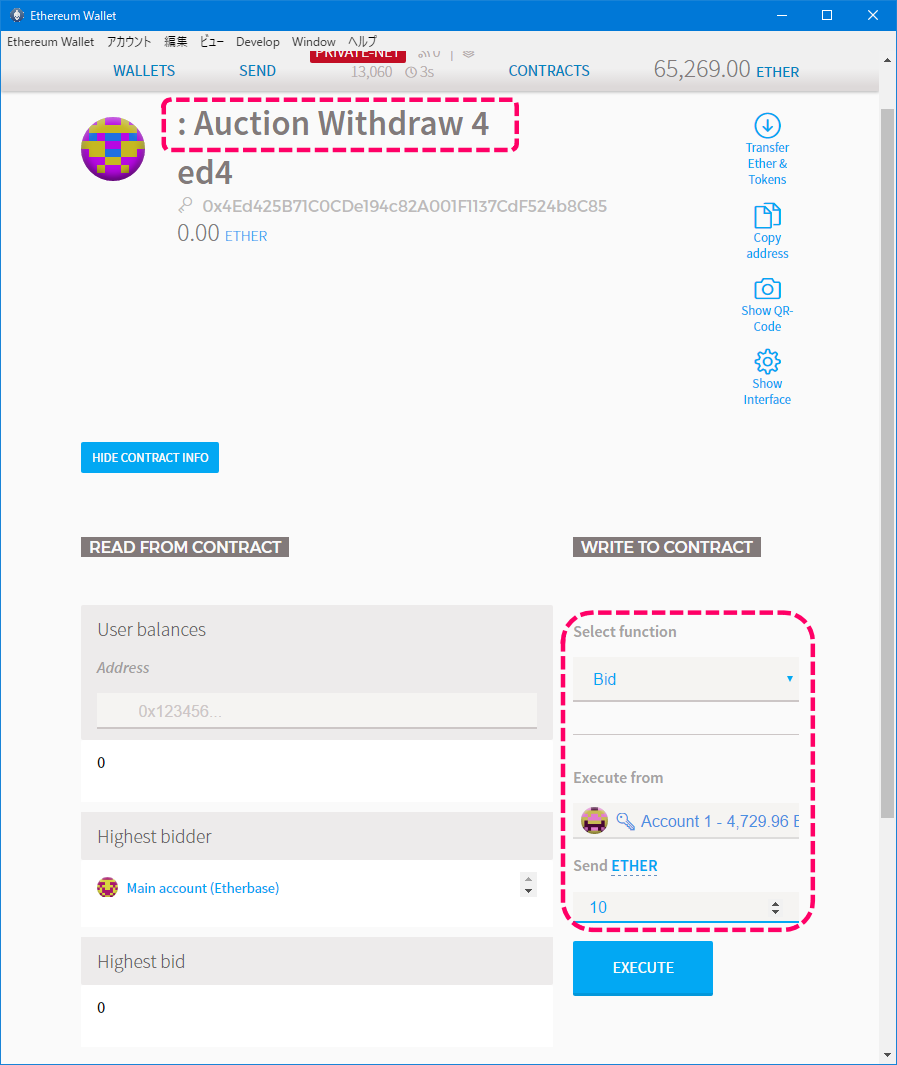
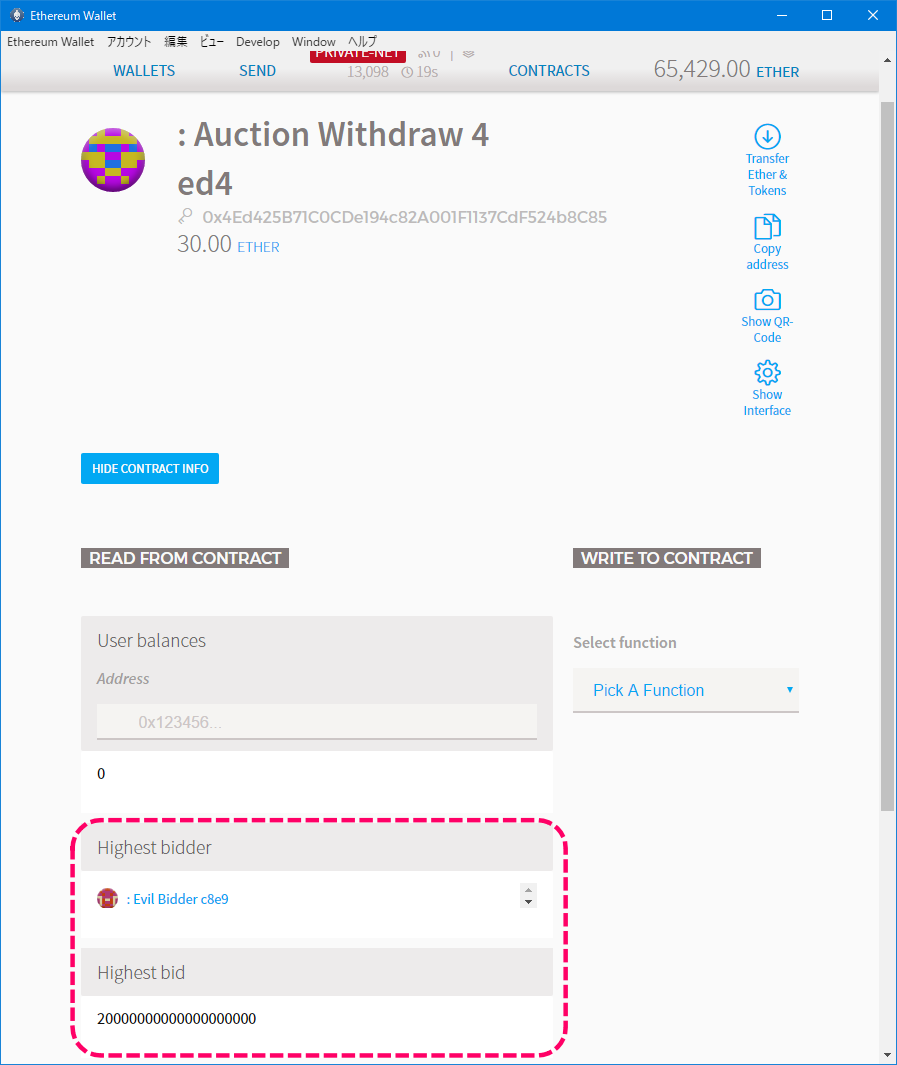
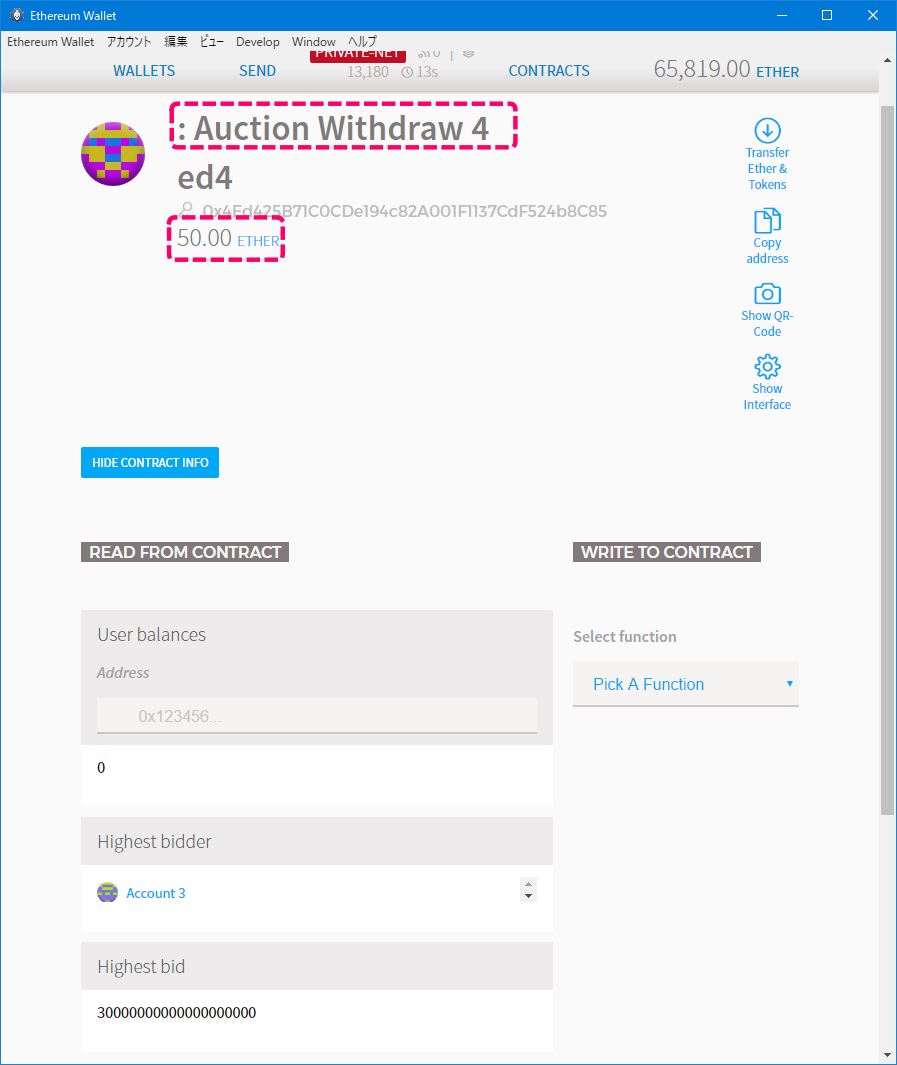
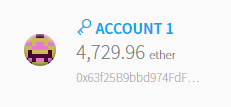
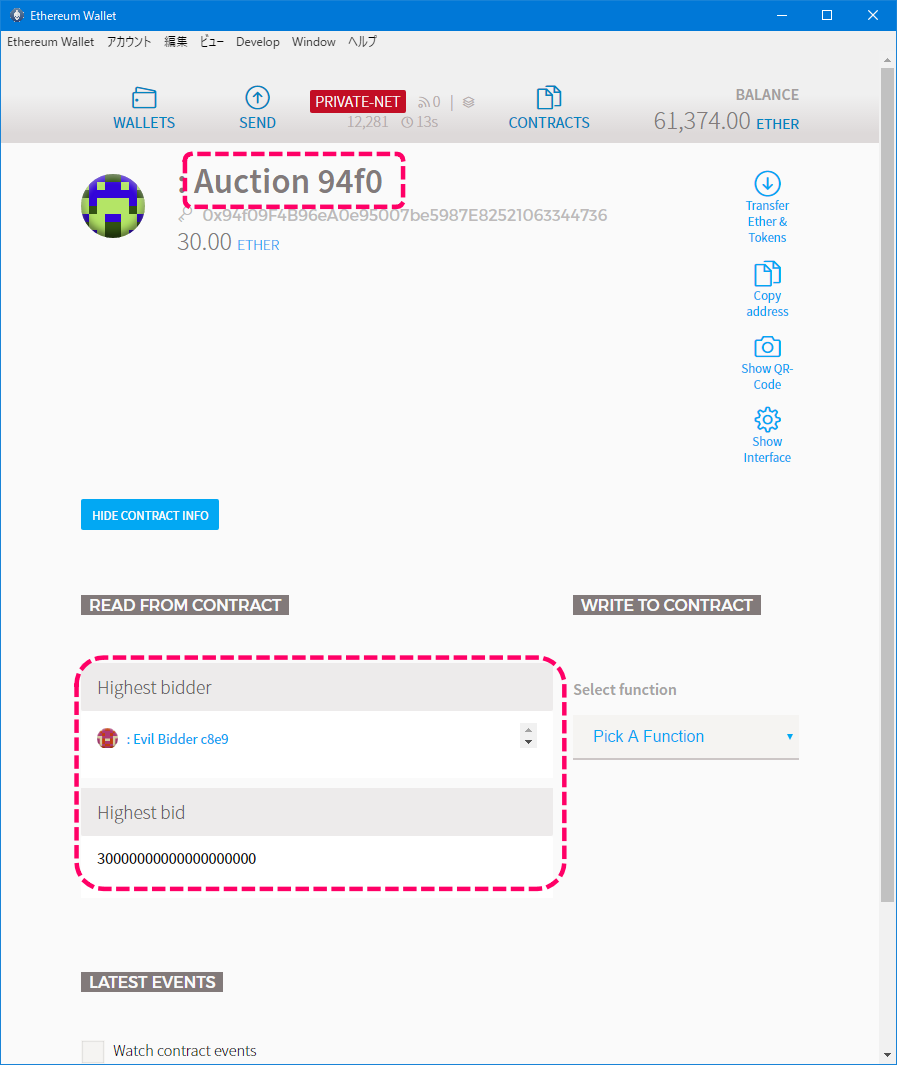
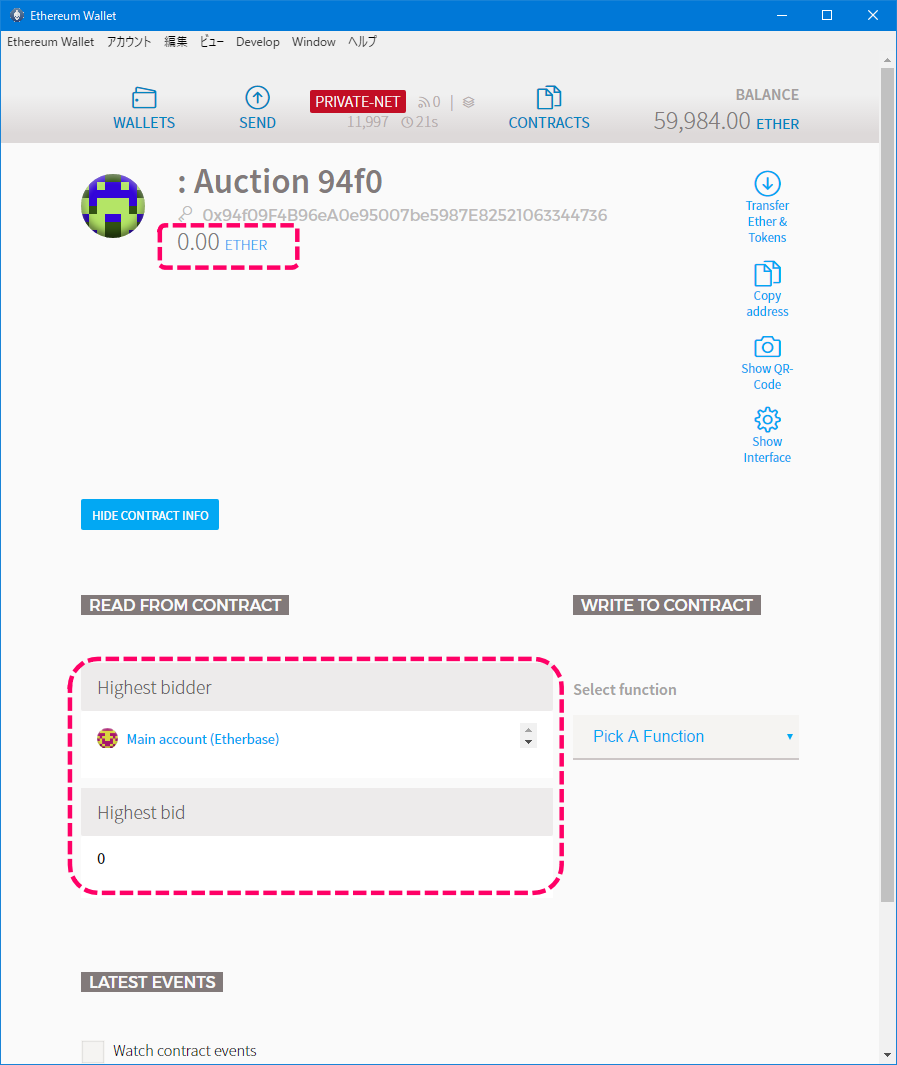
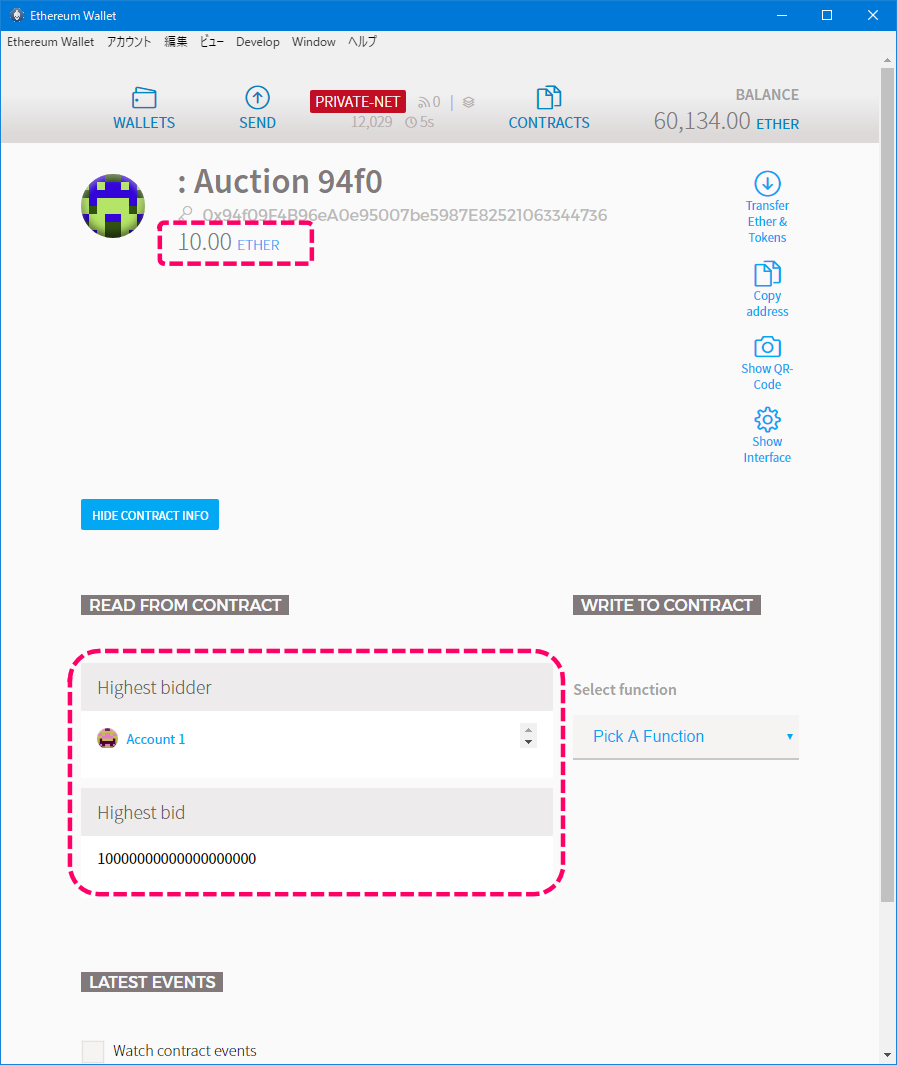
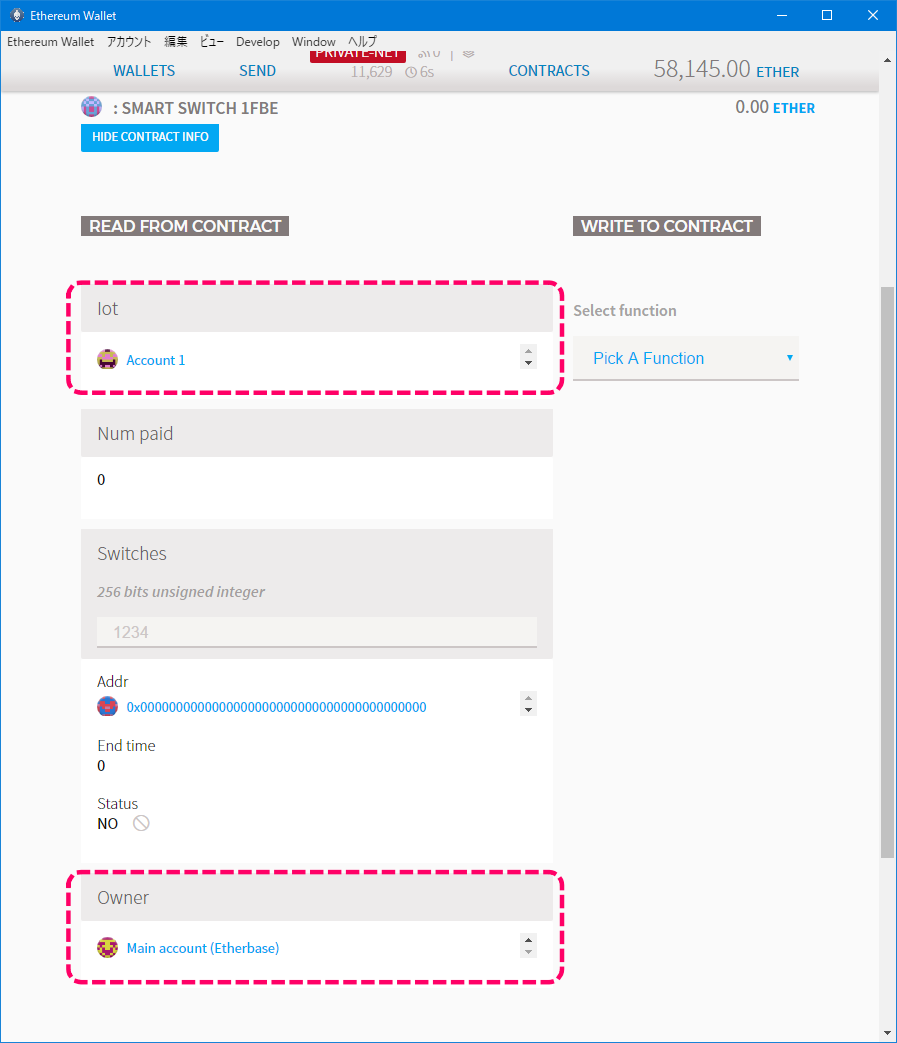
デプロイ後のコントラクトの状態を確認します。

[コントラクトの状態]

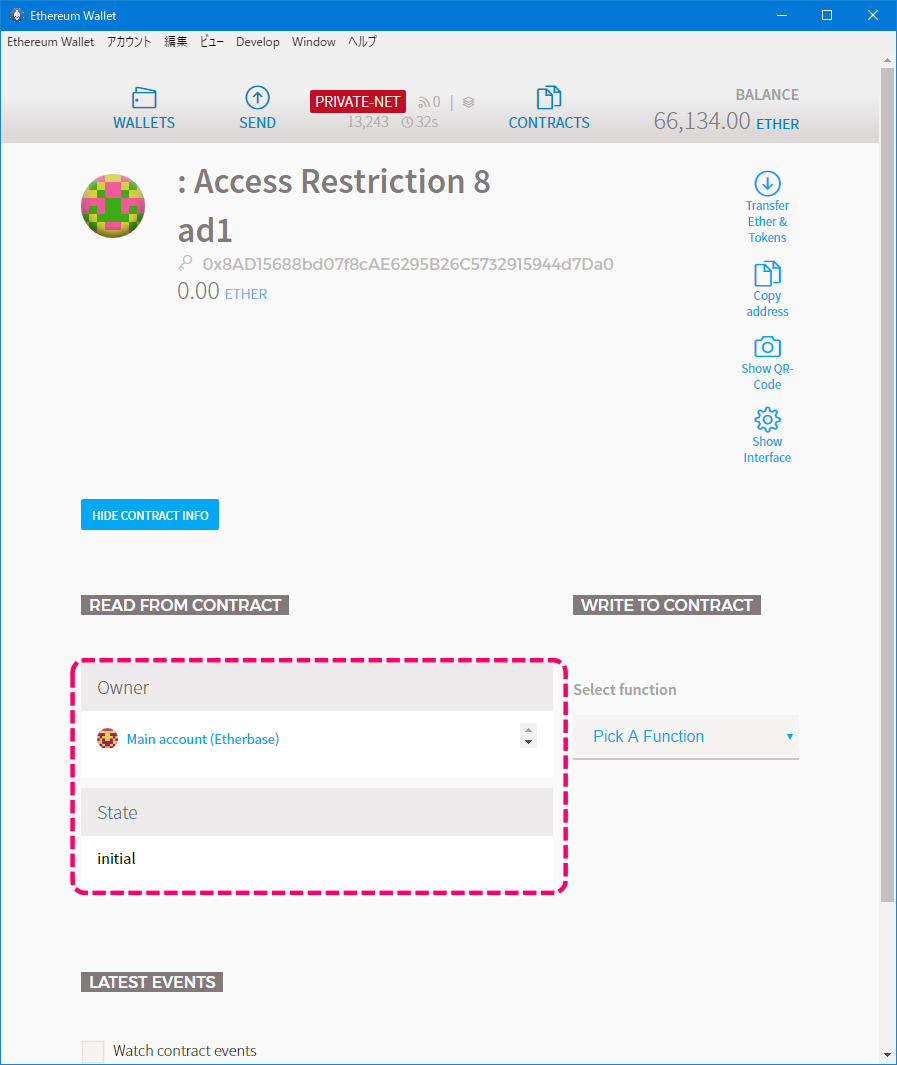
オーナーがMAIN ACCOUNTで、ステートがinitialであることが確認できます。

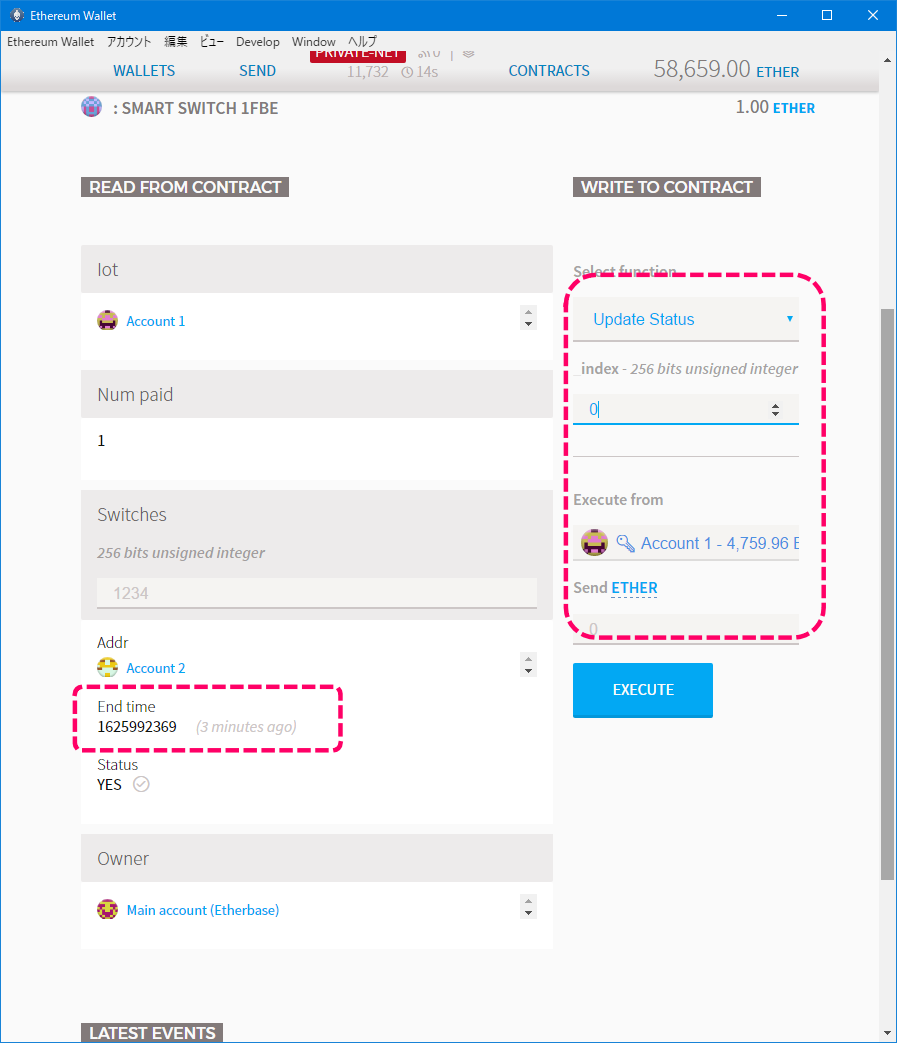
オーナーアドレスからステート更新

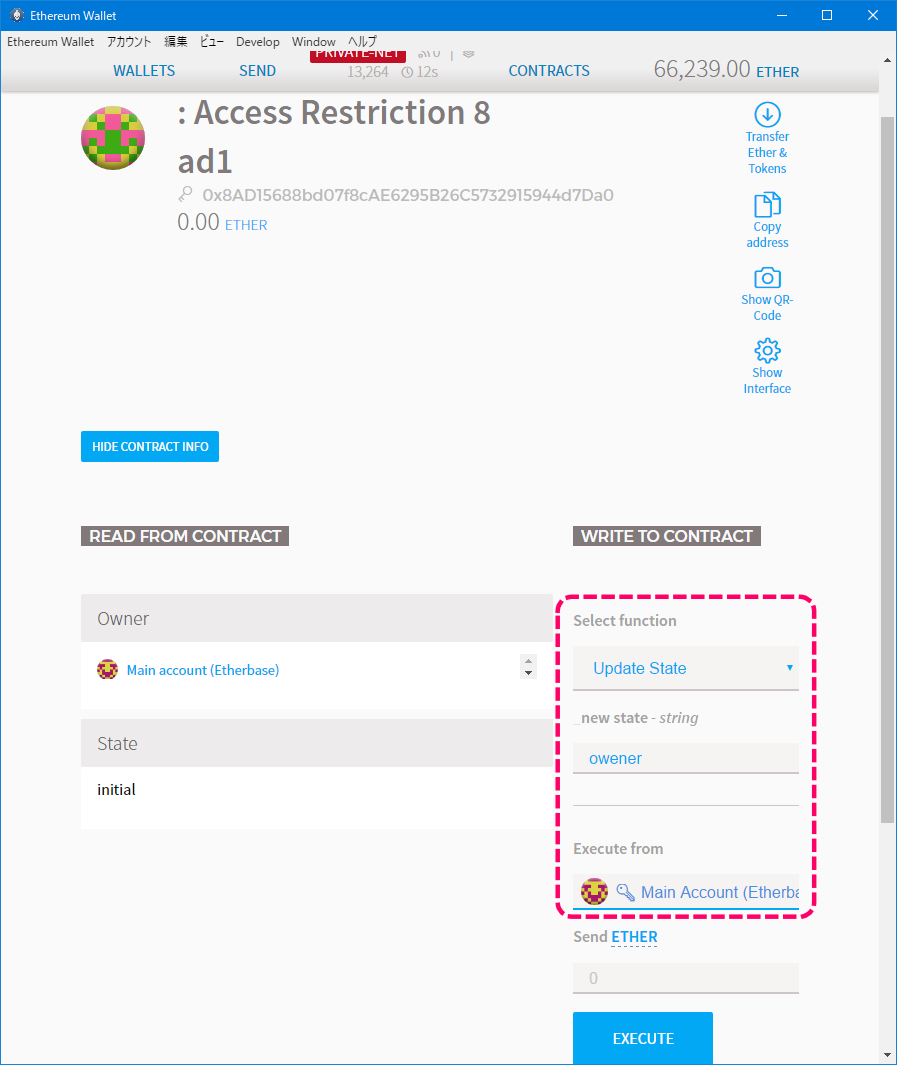
オーナーのMAIN ACCOUNTから、ステートを更新します。(Update State関数)

ステートはowenerです・・・スペリングを間違えました😥

[ステート更新]

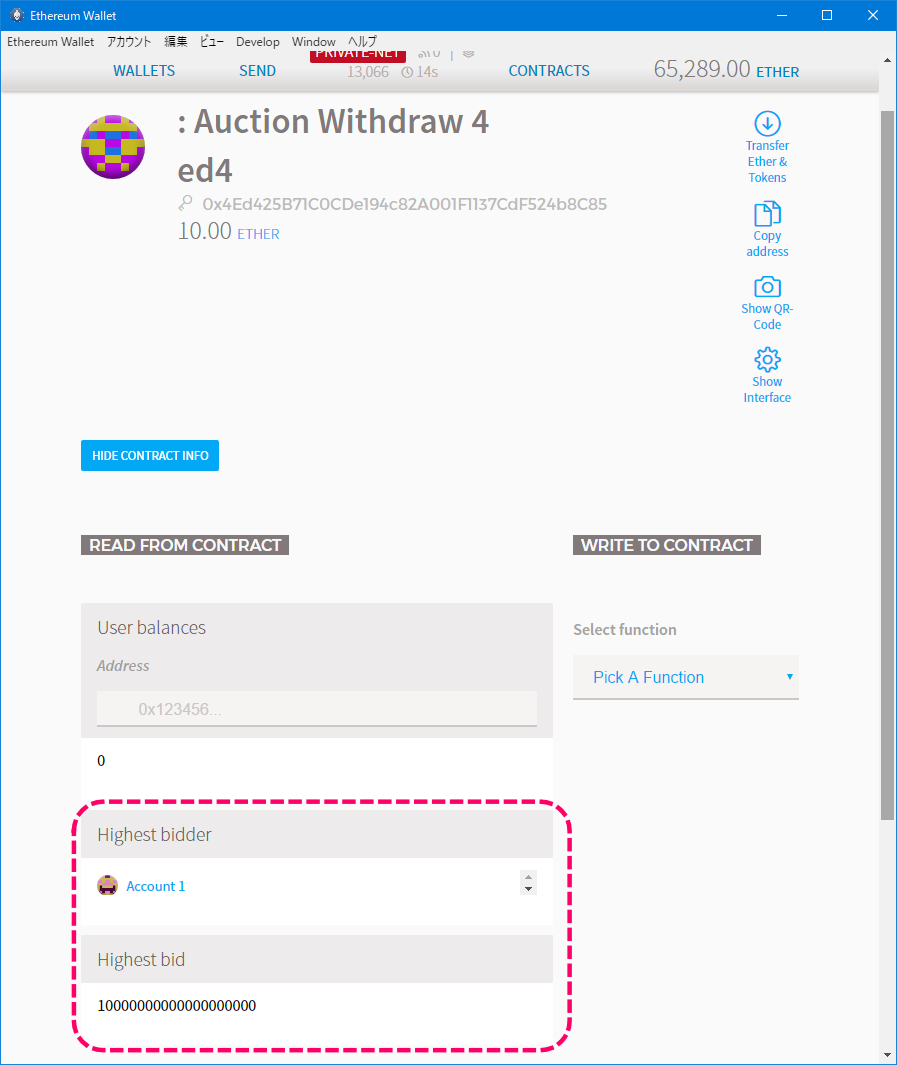
コントラクトの状態を確認します。

[コントラクトの状態]

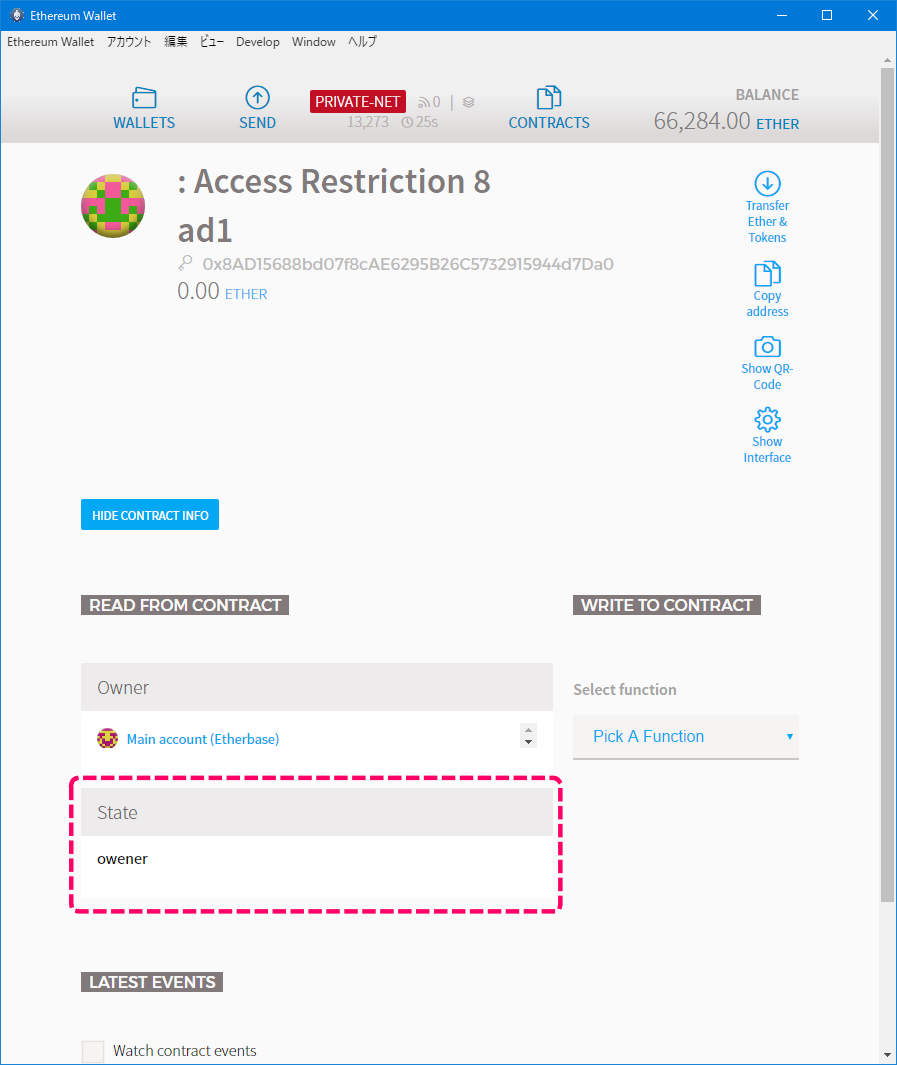
ステートがinitialからowenerに変わっています。

アクセス権のないアドレスから更新

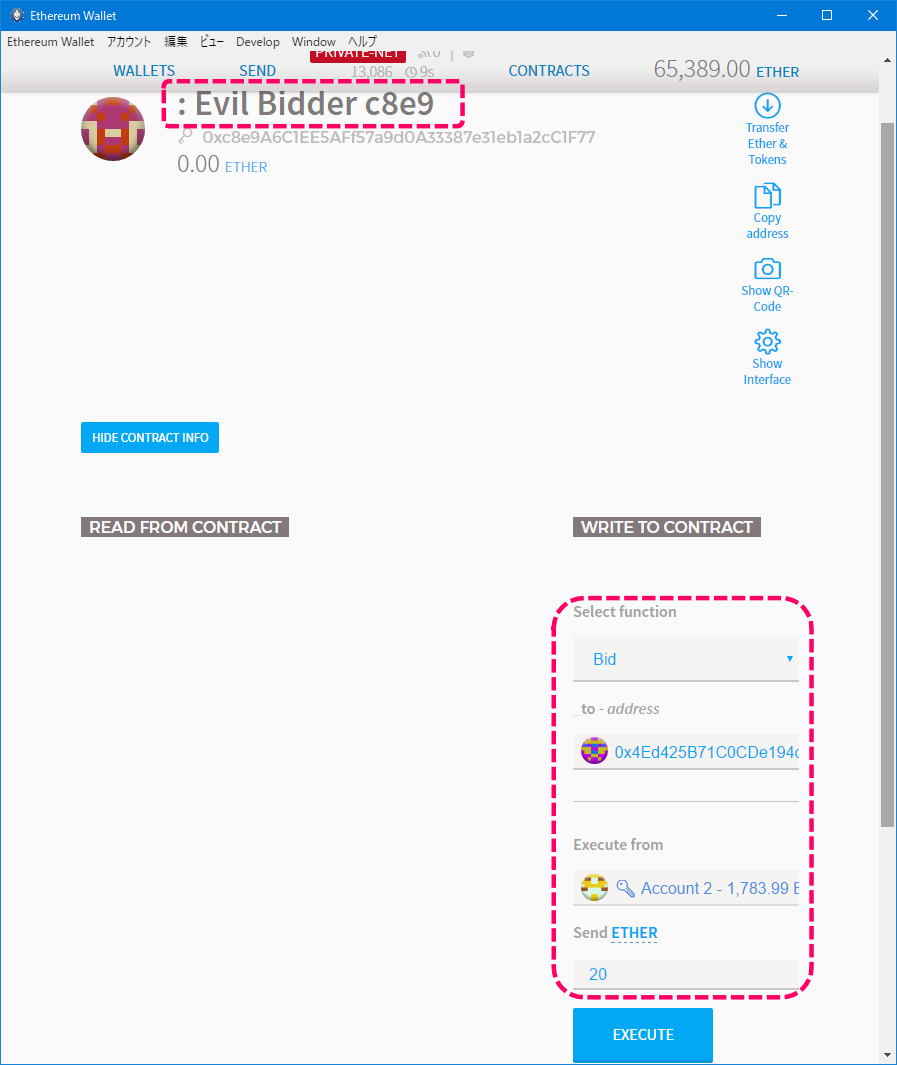
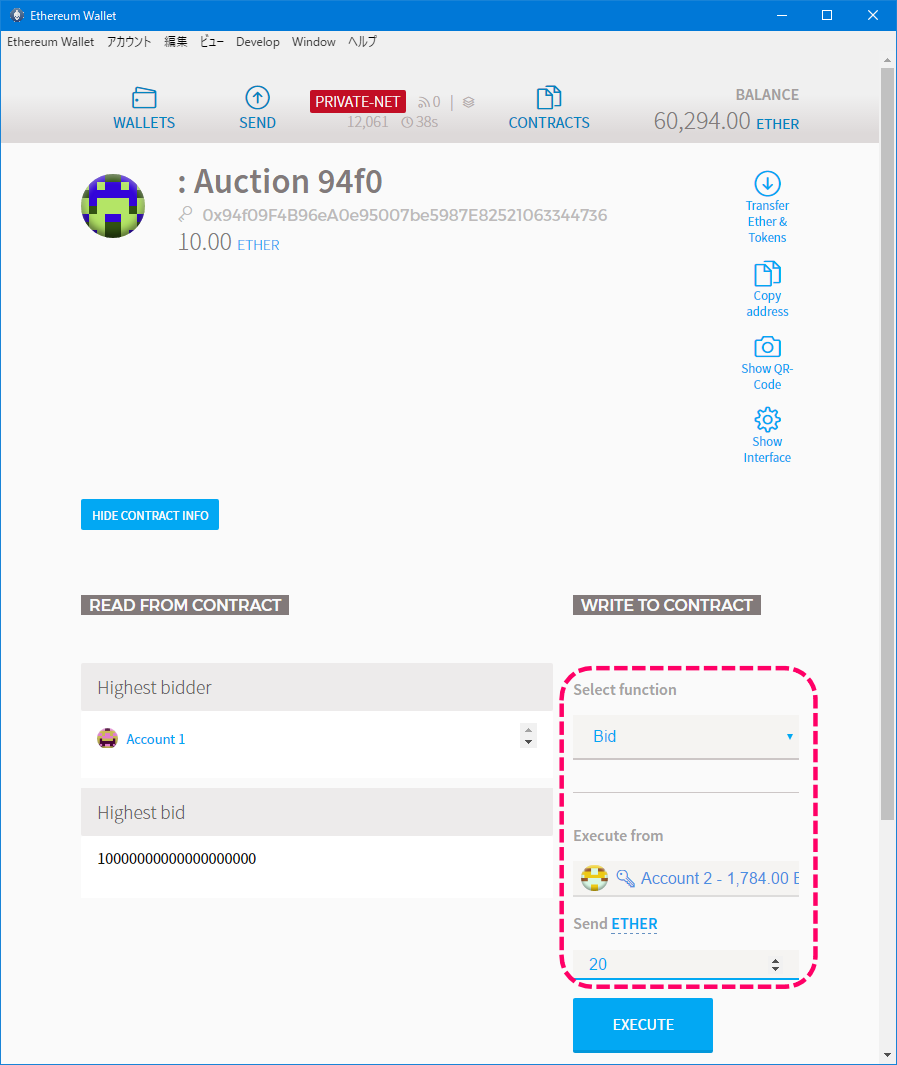
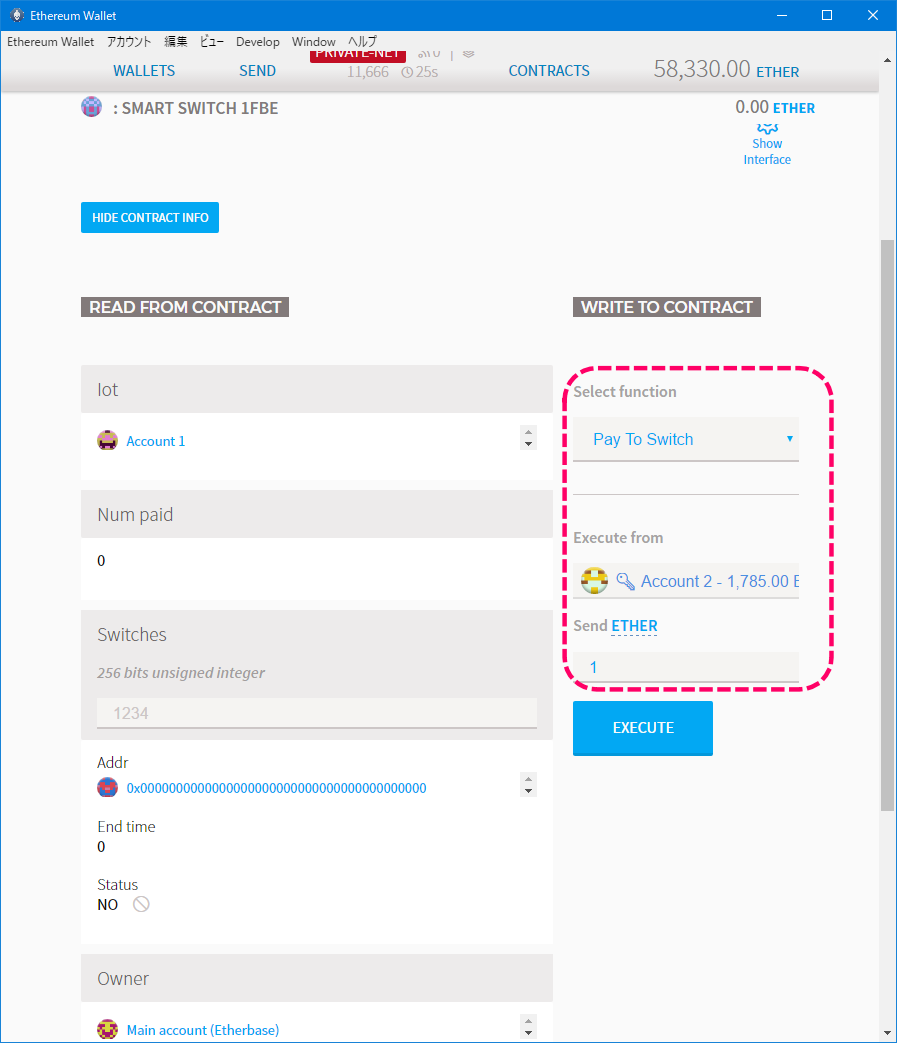
オーナーではないAccount1からステートを変更してみます。

ステートはnot ownerを設定してみました。

また最大消費手数料としては5,000,000 weiを指定しました。(EXECUTEボタン押下後のダイアログ画面にて)

[ステート更新]

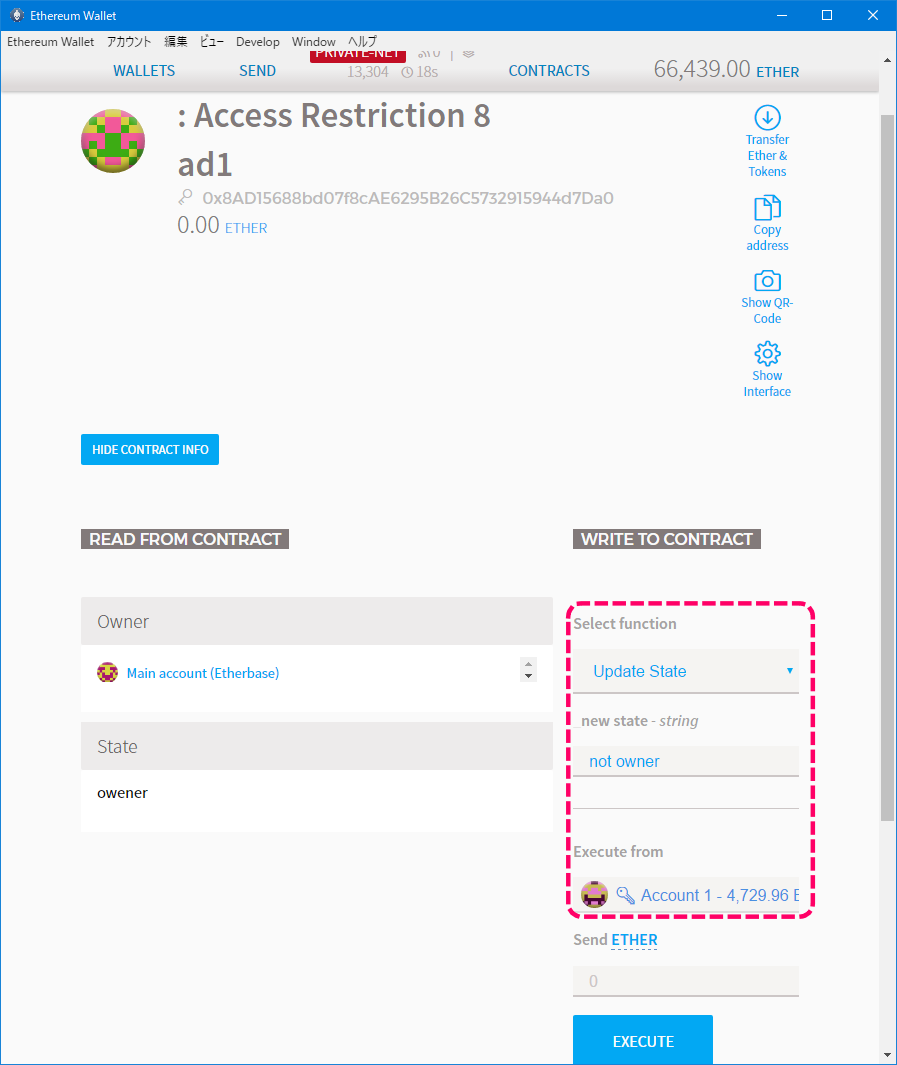
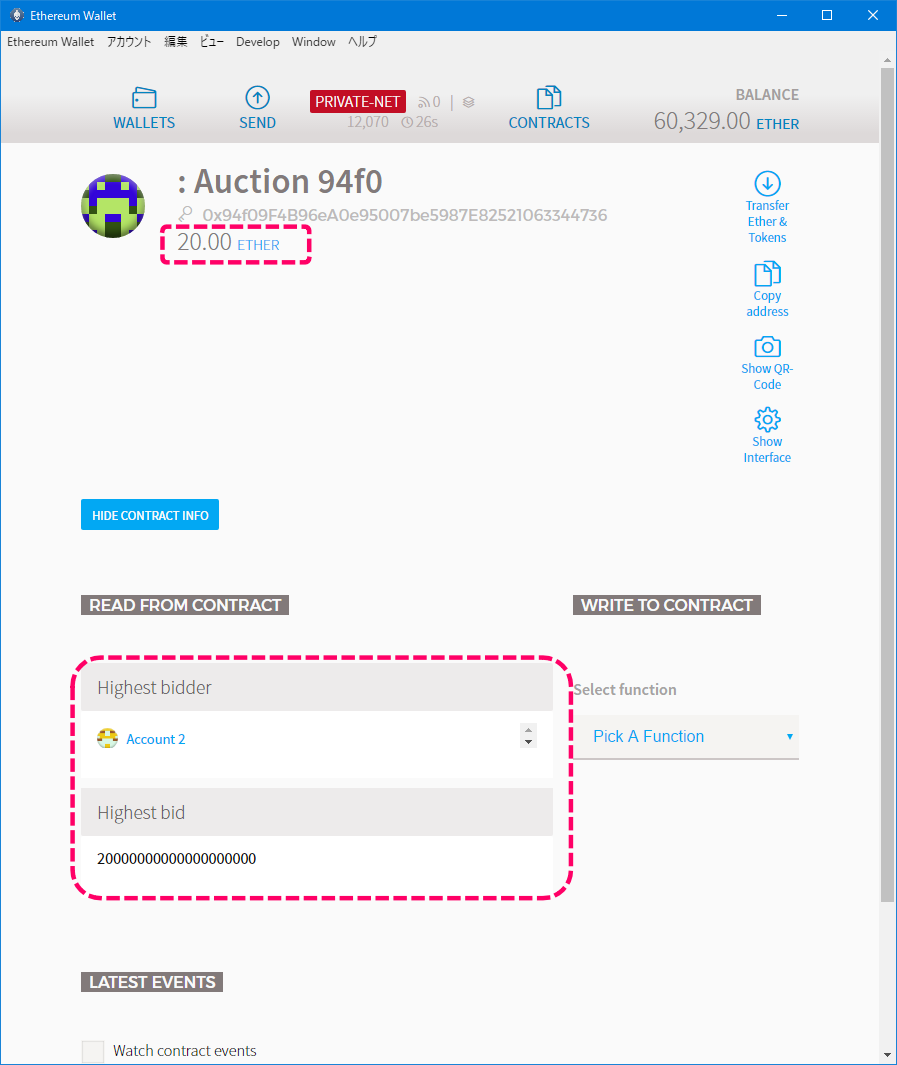
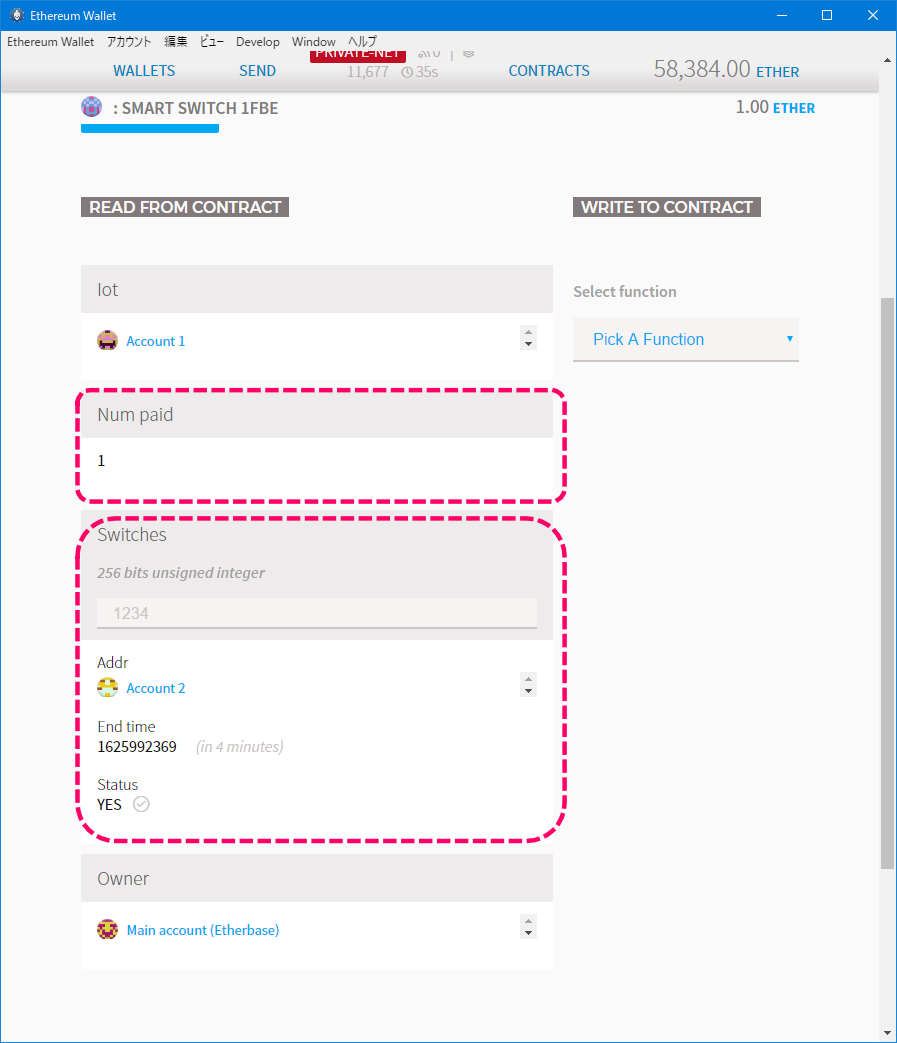
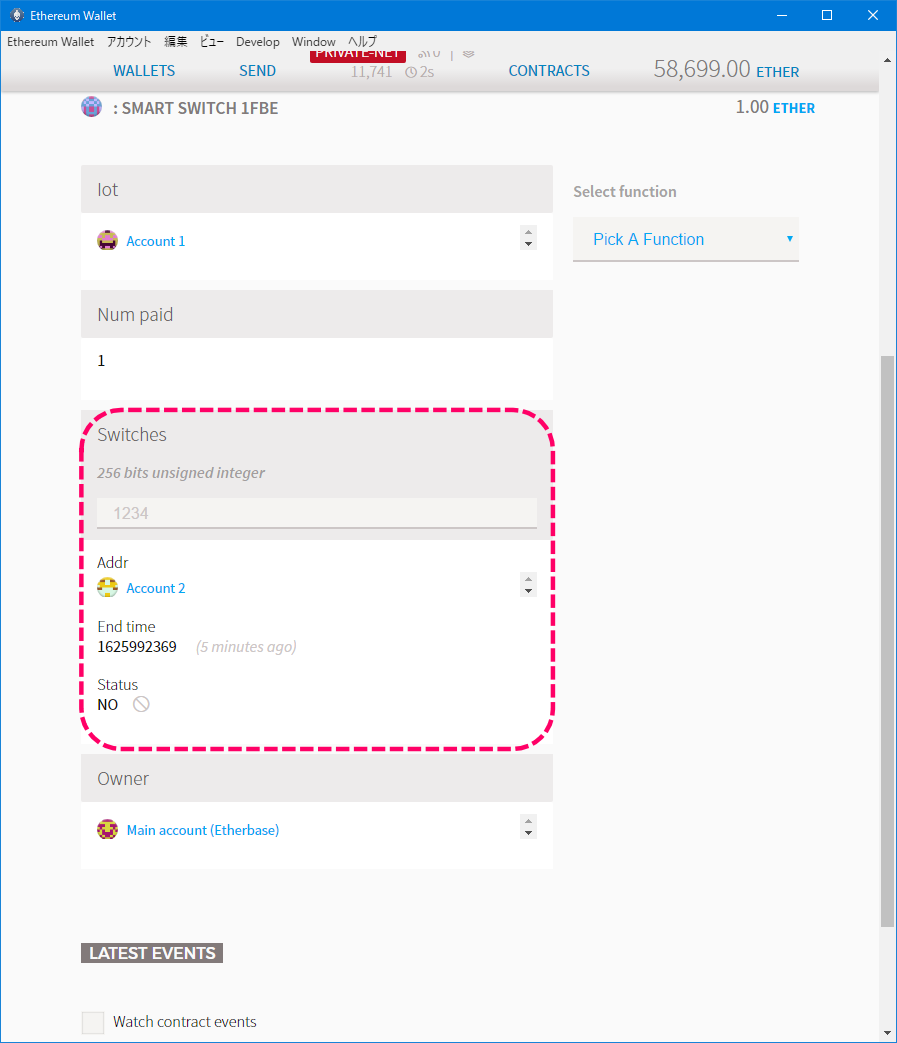
コントラクトの状態を確認します。

[コントラクトの状態]

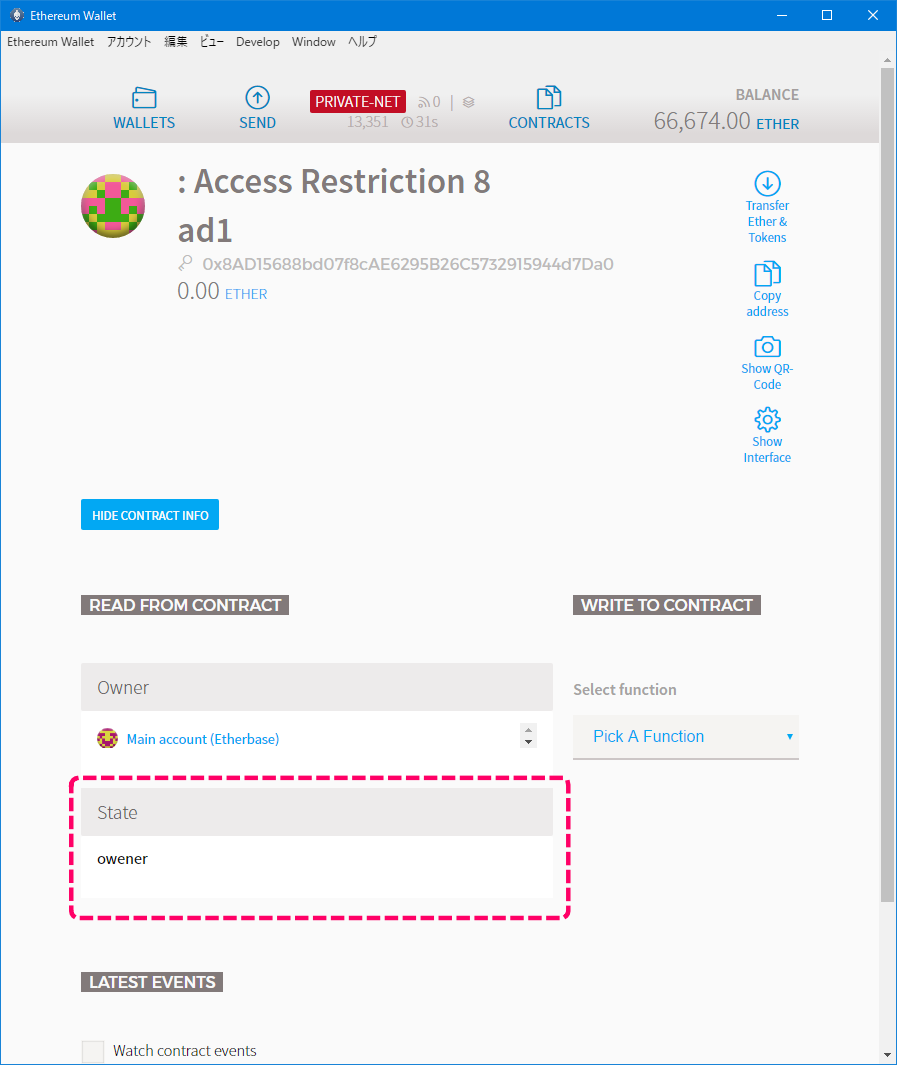
ステートが変わらずowenerであることが確認できます。

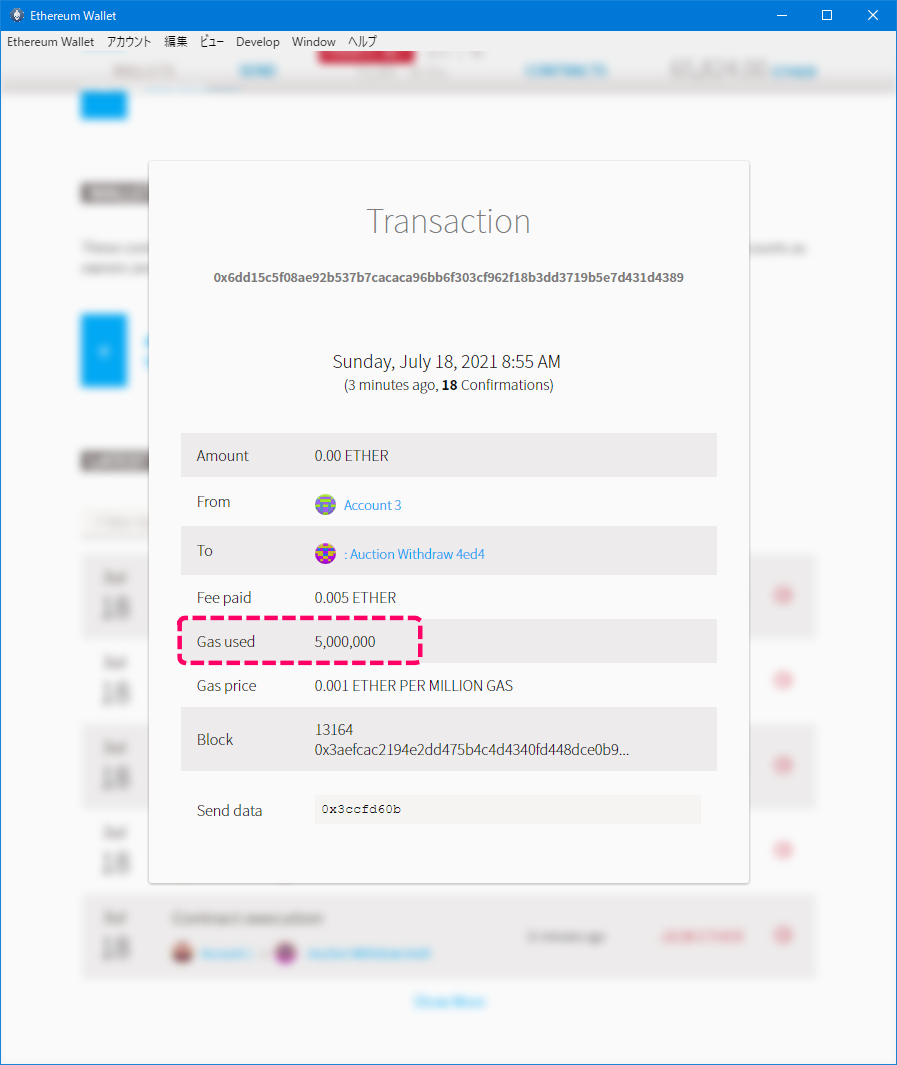
念のためトランザクションの内容も確認します。

[トランザクションの結果]

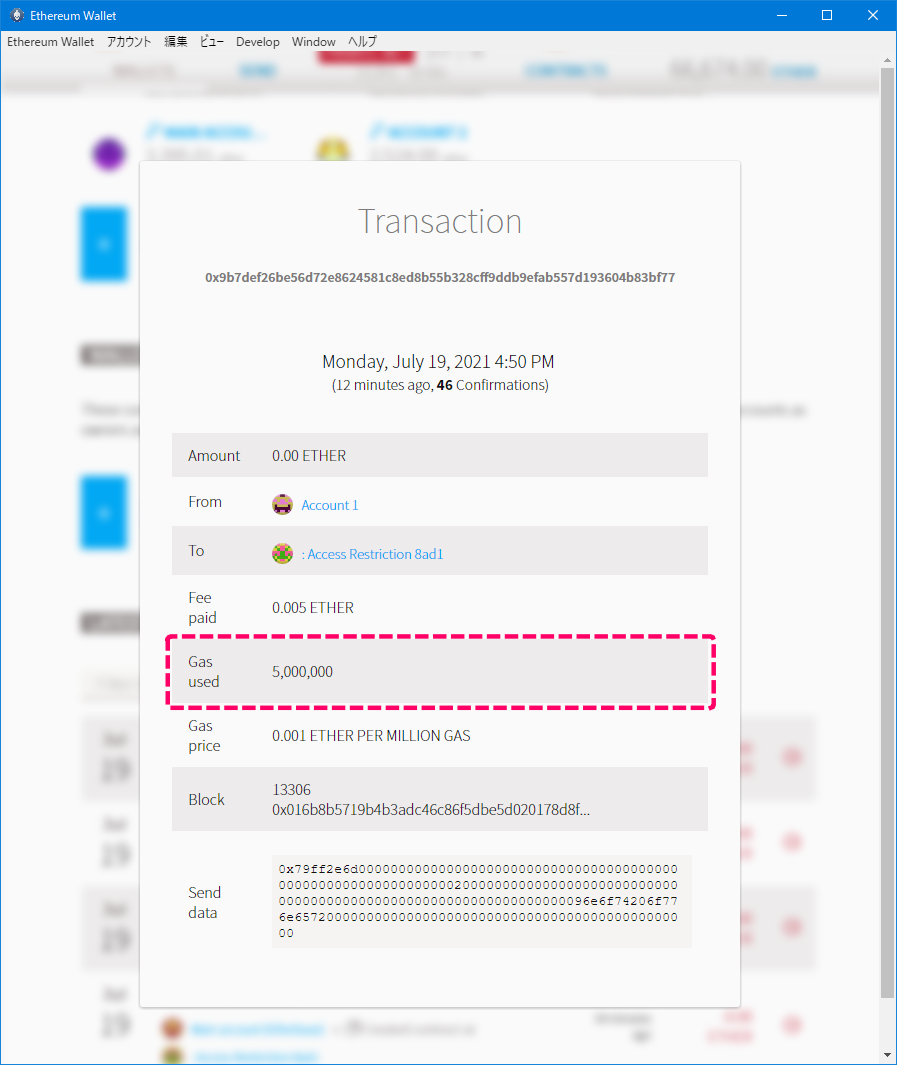
Gas Usedが5,000,000 weiとなっており、手数料が最大で消費されているのでこのトランザクションが失敗したことを再確認できます。

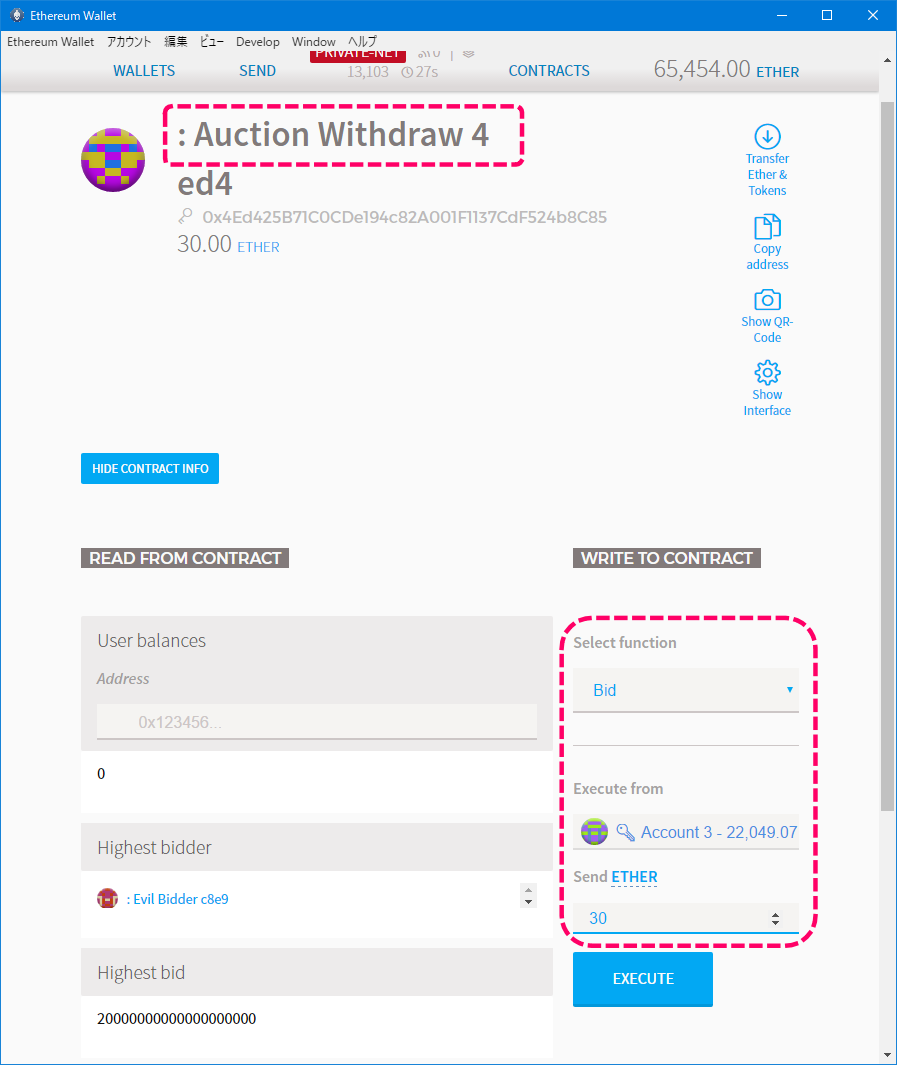
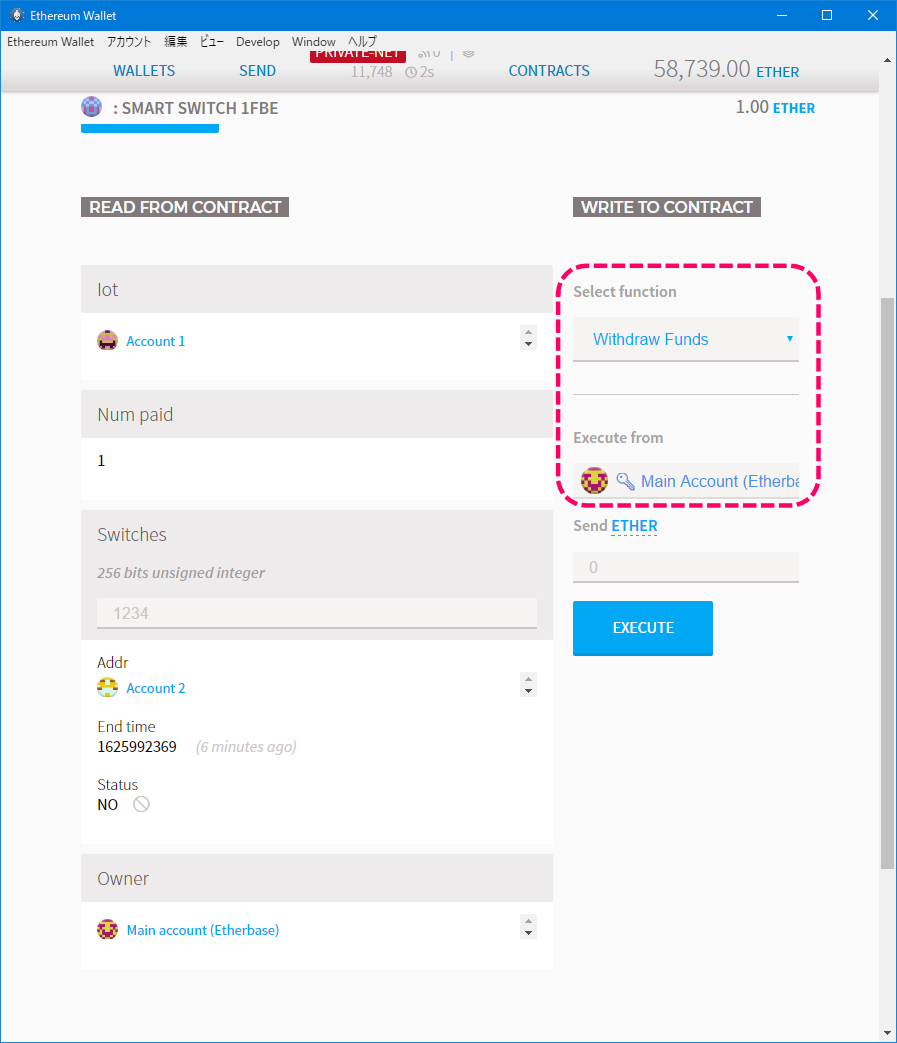
オーナー変更

コントラクトのオーナーを変更します。（MAIN ACCOUNT ⇒ Account1）

Change Owner関数を選んで、new ownerにはAccount1のアドレスを入力します。

この処理はアクセス制限によりオーナーのみが実行できるので、Execute fromにはMAIN ACCOUNTを指定します。

[オーナー変更]

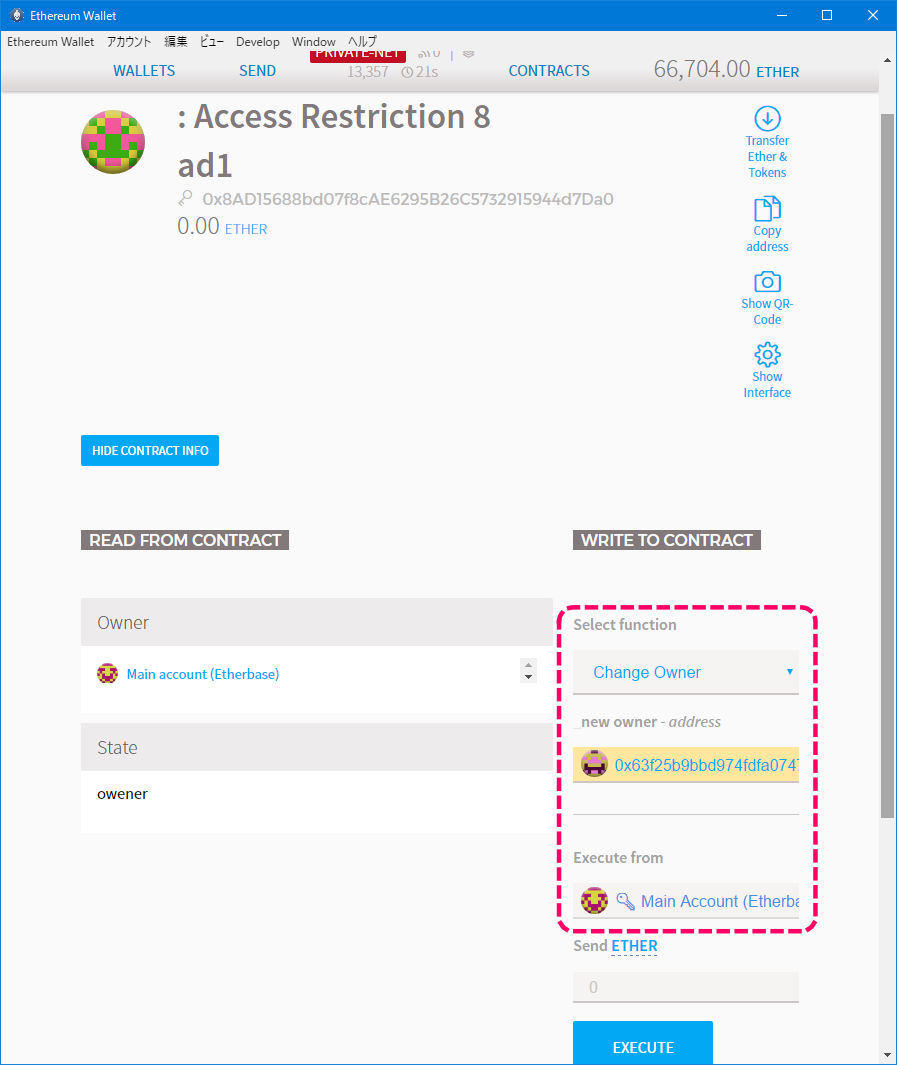
コントラクトの状態を確認します。

[コントラクトの状態]

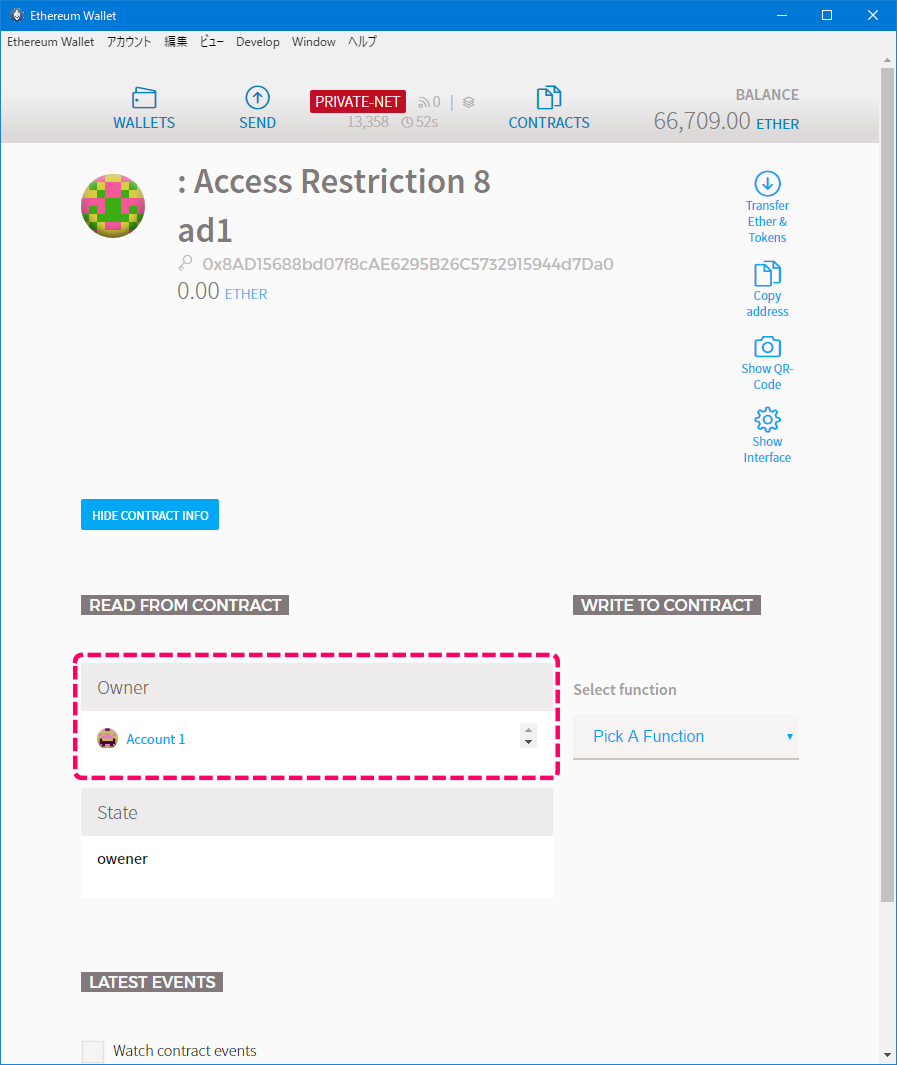
ちゃんとオーナーがAccount1に変更されています。

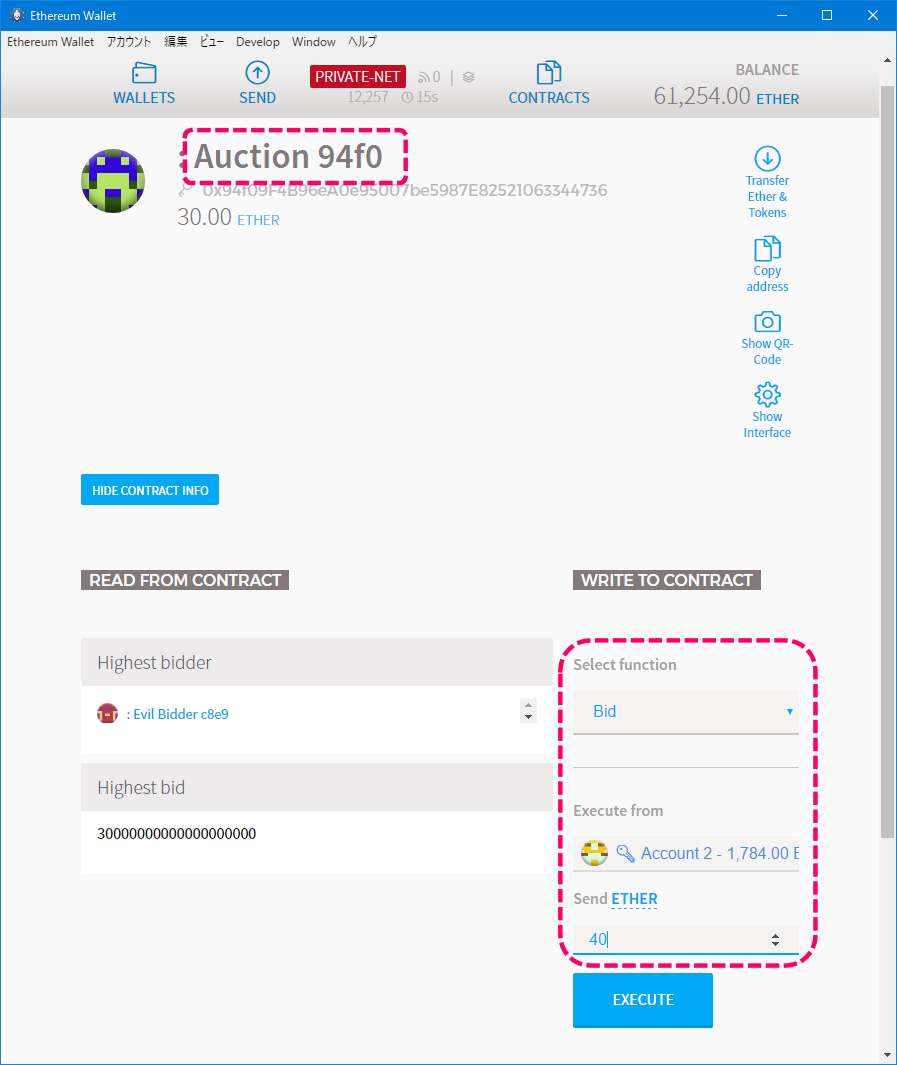
２番目のオーナーからステート更新

オーナーがAccount1に変更されてたので、Account 1からステート変更を行えるかどうか確認します。

Update State関数を選択し、new stateにnew ownerを入力します。

Execute fromはもちろんAccount1です。

[ステート更新]

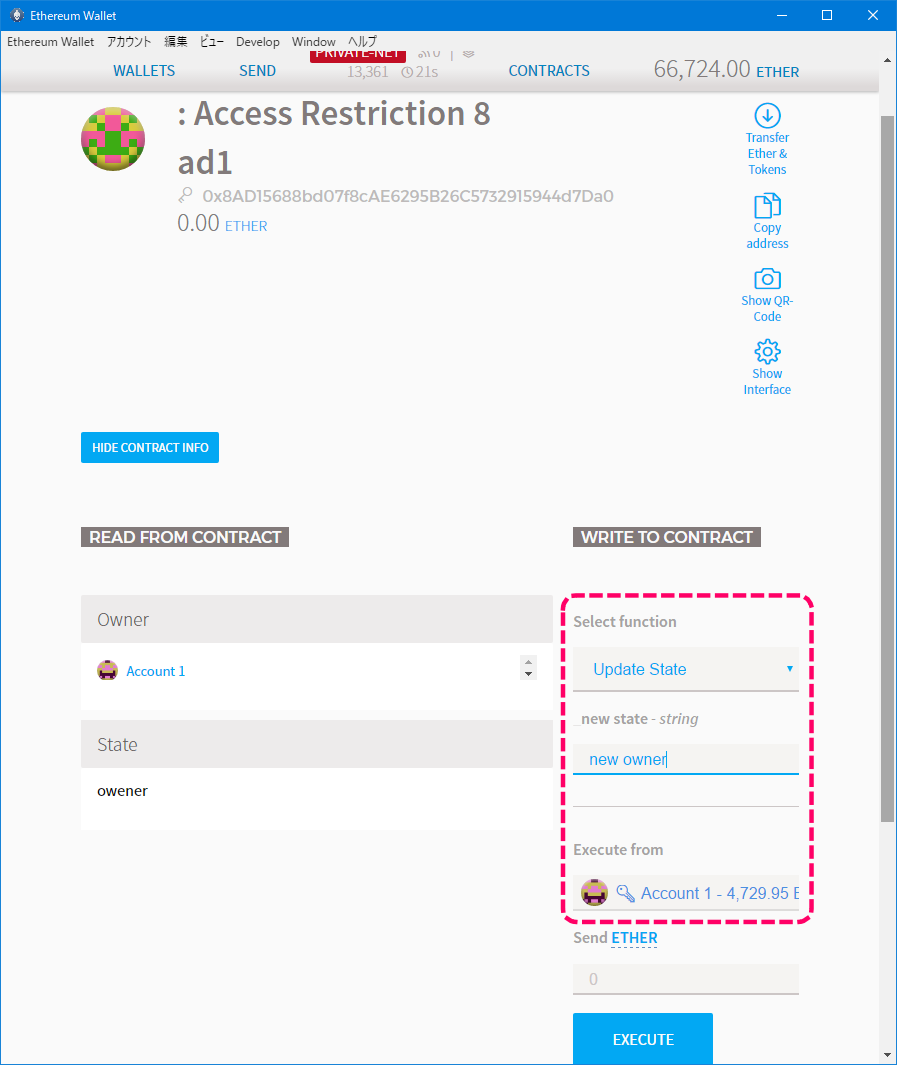
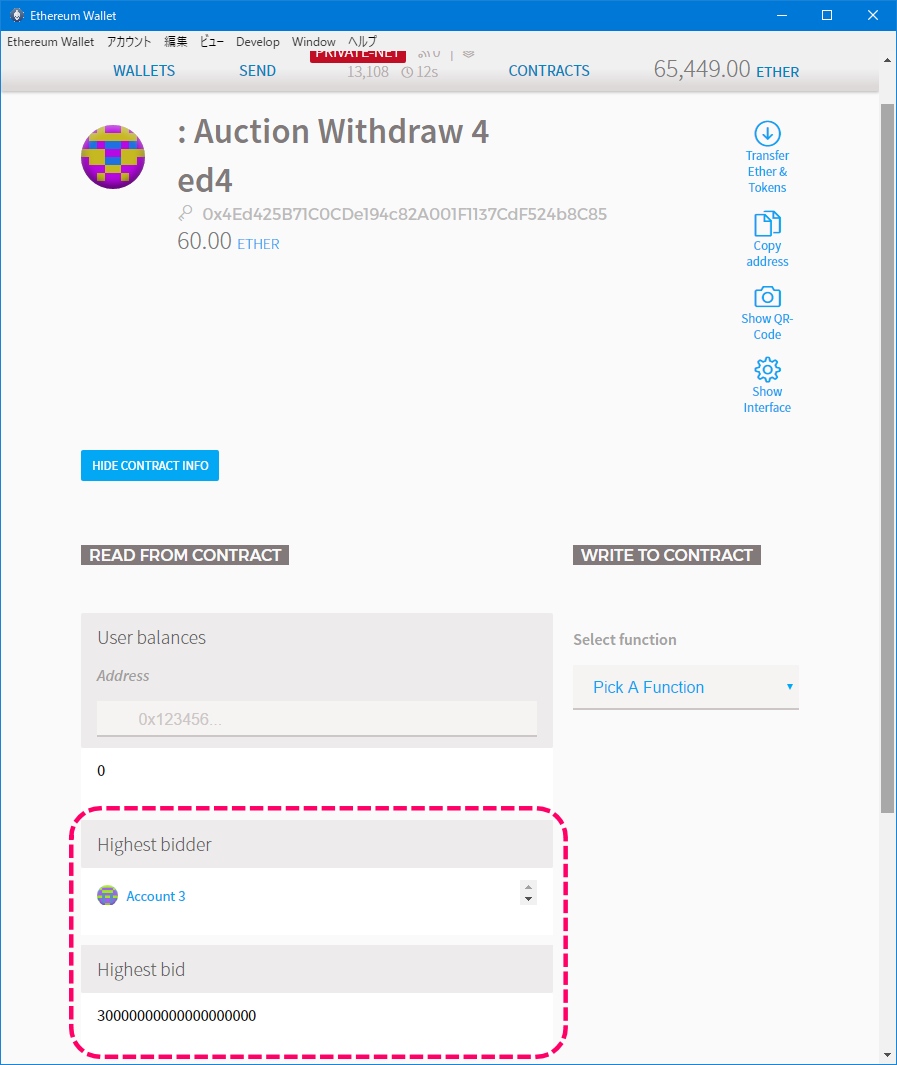
コントラクトの状態を確認します。

[コントラクトの状態]

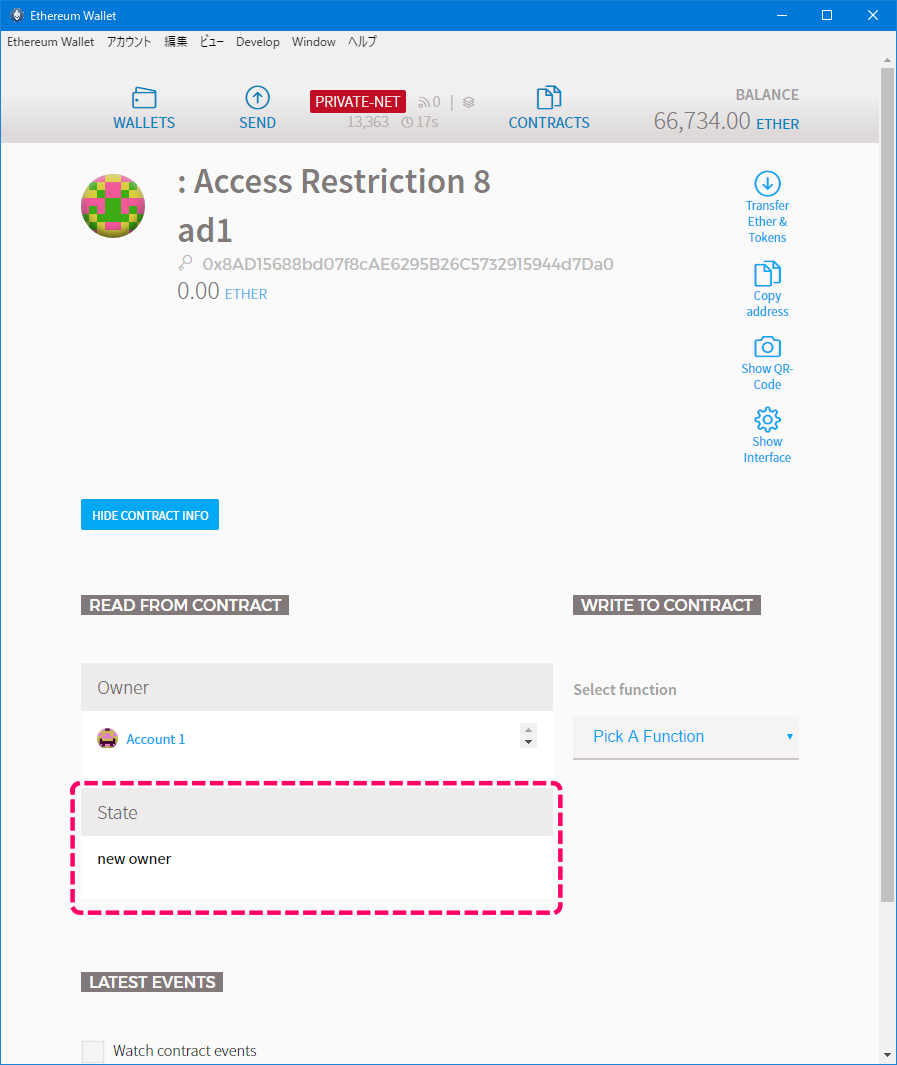
ステートがnew ownerに変更できています。

以上で、アクセス制限のあるコントラクトの動作確認は完了です。

アクセス制限のポイント

関数をpublicで公開することは攻撃表面（リスク）を大きくするので、公開は最小限にするべきです。

また特定のアドレスのみが利用する関数については、必ずアドレスによるアクセス制限を付与しましょう。

アクセス制限のポイントをまとめます。

• アクセス制限はmodifierにて実装する。
• 可能な限り関数は公開しない。
• 特定のアドレスからの呼び出しを想定している関数は、必ずアドレスによる制限を設ける。
• オーナー変更用の関数を用意する。
• ひな形化しておき継承してコントラクトを作成する。

今回は、アクセス制限を行うスマートコントラクトを実装します。

アクセス制限の例としては、コントラクトを生成したアドレスからのみ 実行を許可するというケースが挙げられます。

この場合、トランザクション発行アドレスがコントラクトのオーナーのアドレスと一致することを確認する必要があります。

実装

アクセス制限をする場合、modifierを利用すると関数ごとにアクセス制限を実装する必要がなくなり、コードがシンプルになります。

次のような２つのコントラクトを作成します。

• Ownedコントラクト
  親コントラクトです。
  アクセス制御に関する関数とmodifierを定義しています。
• AccessRestrictionコントラクト
  子コンストラクトです。
  Ownedコントラクトを継承しています。
  文字列のステートを１つ持ち、オーナーだけがそのステートを変更することができます。

[ソースコード]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

pragma solidity ^0.4.11;
contract Owned {
    address public owner;

    /// アクセスチェック用のmodifier
    modifier onlyOwner() {
        require(msg.sender == owner);
        _;
    }

    /// オーナーを設定
    function owned() internal {
        owner = msg.sender;
    }

    /// オーナーを変更
    function changeOwner(address _newOwner) public onlyOwner {
        owner = _newOwner;
    }
}

// 継承
contract AccessRestriction is Owned{
    string public state;

    /// コンストラクタ
    function AccessRestriction() {
        // Ownedで定義されているowned関数をコール
        owned();

        // stateの初期値を設定
        state = "initial";
    }

    /// stateを更新する関数
    function updateState(string _newState) public onlyOwner {
        state = _newState;
    }
}

アクセス制限に関する処理は以下の通りです。

• modifier onlnOwner (6-9行目)
  アクセス制限用のmodifierで、アクセス制限をしたい関数に付与します。
• owned (12-14行目)
  オーナーを指定するための関数です。
  子コンストラクトから呼ばれることを想定しているためinternalとしています。
• changeOwner (17-19行目)
  オーナーを変更する場合に利用する関数です。
  現オーナーからの呼び出しのみ許可します。

次回は、このアクセス制限のあるコントラクトの動作確認を行います。

今回は、攻撃を回避するオークション用スマートコントラクトを実行していきます。

アカウントごとの役割

アカウントの役割は次の通りです。

• MAIN ACCOUNT (eth.accounts[0]) “0xec3b01f36b44182746ca109230567c4915512e35”
  オークションの オーナー。
• ACCOUNT1 (eth.accounts[1]) “0x63f25b9bbd974fdfa07477cb99c60d2073cfe560”
  Bidder1（入札者１）。アカウント１。
  最初の入札を行う。
• ACCOUNT2 (eth.accounts[2]) “0xd5adf1e9fbc1ed869ed4c7372961238fddc760a5”
  Bidder2（入札者２）。アカウント２。⇒悪意のあるコンストラクトから攻撃を行う。
  ２回目の入札を行う。
• ACCOUNT3 (eth.accounts[3]) “0xe62be181791eb0add680739299165ec444e2eb73”
  Bidder3（入札者３）。アカウント３。
  ３回目の入札を行う。
• ACCOUNT4 (eth.accounts[4])
  マイナー。

デプロイ

まずはデプロイを行います。デプロイアカウントはMAIN ACCOUNTです。

[デプロイ時のイメージ]

１回目の入札(アカウント１)

アカウント１から10 etherを入札します。

[１回目の入札]

入札後のコントラクトの状態は下記のとおりです。

[コントラクトの状態]

最高額提示者がアカウント１で、最高掲示額が10 ehterになっていることが確認できます。

入札を行ったアカウント１の残高を確認します。

[アカウント１の残高]

10 ether減っていることが分かります。

２回目の入札（アカウント２・悪意のあるコントラクト）

悪意のあるコントラクトから20 etherを送金します。アカウント２を使用します。

to - addressには、送金先のオークション用コントラクトのアドレスを設定します。

[２回目の入札（悪意のあるコントラクトから）]

送金後のコントラクトの状態は下記のとおりです。

[コントラクトの状態]

最高額提示者がEvil Bidder(悪意のあるコントラクト)で、最高掲示額が20 ehterになっていることが確認できます。

送金を行ったアカウント２の残高を確認します。

[アカウント２の残高]

20 ether減っていること分かります。

３回目の入札（アカウント３）

アカウント３から30 etherを入札します。

改善前のオークション用コントラクトでは、悪意のあるコントラクトから送金後、一切入札ができなくなってしまったのでここで入札できれば問題が解消されているということになります。

[３回目の入札]

入札後のコントラクトの状態は下記のとおりです。

[コントラクトの状態]

最高額提示者がアカウント３で、最高掲示額が30 ehterになっていることが確認できます。

入札できなくなるという問題が解消されています。

入札を行ったアカウント３の残高を確認します。

[アカウント３の残高]

30 ether減っていることが分かります。

アカウント１の返金

返金処理を確認します。

アカウント１から返金の操作を行います。

[アカウント１の返金]

返金処理後のコントラクトの状態を確認します。

[コントラクトの状態]

60 etherから50 etherに減っていることが確認できます。

アカウント１の残高も確認しておきます。

[アカウント１の残高]

問題なく10 ether返金されています。

アカウント２の返金

悪意のあるコントラクトに返金リクエスト用の関数を定義していないので省略します。

アカウント３の返金

アカウント３は最高金額提示者なので返金できないのですが、一応返金されないことを確認します。

[アカウント３の返金]

返金処理後のコントラクトの状態を確認します。

[コントラクトの状態]

50 etherのまま変わっていませんので、返金されなかったということになります。

念のため、アカウント３の残高を確認します。

[アカウント３の残高]

やはり残高の増減はありません。

参考までに処理が実行されなかったことは、トランザクションのGasがすべて消費されていることでも確認できます。

アカウント３の返金処理では5000000weiを最大手数料(Provide maximum fee)として設定していました。

返金処理のトランザクション実行結果を確認します。

[トランザクションの実行結果]

Gas usedが5,000,000となっていて、指定した最大手数料が消費されているので処理が失敗しているということになります。

以上で、攻撃を回避するオークション用コントラクトの動作確認は完了となります。

今回は攻撃を回避するためのオークション用スマートコントラクトを実装していきます。

回避策

攻撃を回避するためにはどのような仕様にすればよいでしょうか。

入札(bid)と同時に返金を行うと、返金時に問題が発生し入札自体が失敗してしまうことがあるので、入札と返金の処理を分ける仕様にしてみたいと思います。

実装

入札と返金の処理を分けたコードは次の通りです。

[ソースコード]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

pragma solidity ^0.4.11;
contract AuctionWithdraw {
    address public highestBidder;  // 最高額提示アドレス
    uint public highestBid;        // 最高提示額
    // 返金額を管理するマップ
    mapping(address => uint) public userBalances;

    /// コンストラクタ
    function AuctionWithdraw() payable {
        highestBidder = msg.sender;
        highestBid = 0;
    }

    /// Bid用の関数
    function bid() public payable {
        // bidが現在の最高額よりも大きいことを確認
        require(msg.value > highestBid);

        // 最高額提示アドレスの返金額を更新する
        userBalances[highestBidder] += highestBid;

        // ステート更新
        highestBid = msg.value;
        highestBidder = msg.sender;
    }

    function withdraw() public{
        // 返金額が0より大きいことを確認
        require(userBalances[msg.sender] > 0);

        // 最高額提示者でないことを確認
        require(userBalances[msg.sender] < highestBid);

        // 返金額を退避
        uint refundAmount = userBalances[msg.sender];

        // 返金額を更新
        userBalances[msg.sender] = 0;

        // 返金処理
        if(!msg.sender.send(refundAmount)) {
            throw;
        }
    }
}

このコードのポイントは、bid部分と返金部分が独立し、もしwithdrawで失敗したとしてもその後の入札(bid)に影響を与えないことです。

まとめ

etherの返金は、送り先のコントラクトに悪意や実装の問題があると予期せぬ動作を引き起こされる可能性があります。

返金をするときは、他の処理とは独立させ返金専用の関数を作り、etherを取りにきてもらうのが安全だということになります。

今回はオークションを攻撃するスマートコントラクトを実行していきます。

アカウントごとの役割

アカウントの役割は次の通りです。

• MAIN ACCOUNT (eth.accounts[0]) “0xec3b01f36b44182746ca109230567c4915512e35”
  オークションの オーナー。
• ACCOUNT1 (eth.accounts[1]) “0x63f25b9bbd974fdfa07477cb99c60d2073cfe560”
  Bidder1（入札者１）。アカウント１。⇒悪意のあるコンストラクトから攻撃を行う。
• ACCOUNT2 (eth.accounts[2]) “0xd5adf1e9fbc1ed869ed4c7372961238fddc760a5”
  Bidder2（入札者２）。アカウント２。
• ACCOUNT3 (eth.accounts[3])
  マイナー。

デプロイ

まずはデプロイを行います。デプロイアカウントはアカウント１です。

[デプロイ時のイメージ]

悪意のあるコントラクトから入札(30 ether)

入札を行う前にアカウント１の残高を確認します。

アカウント１から、悪意のあるコンストラクト(EvilBidder)を使って入札(bid関数)を行います。

入札額は30 etherです。

to - addressには、オークション用コントラクトのアドレスを設定しています。

アカウント１の残高を確認します。

30 ether減っていることが確認できます。

攻撃された後のオークション用コントラクト

オークション用コントラクトの状態を確認します。

最高提示額が30 etherになっていることが確認できます。

また最高額提示者がEvilBidderのアドレスになっていることも確認できます。

通常の入札(40 ether)

アカウント２から再び入札を行います。

入札額は40 etherです。

オークションコントラクトの状態を確認します。

最高入札額が30 etherで、最高額提示者がEvilBidderのアドレスになっていることから、40 etherの入札が失敗していることを確認できます。

入札が失敗した理由

入札失敗の流れは次の通りです。

1. オークション用コントラクトのbid関数がコールされる。
2. 最高提示額が更新されたため、オークションコントラクトから悪意のあるコントラクトへ返金処理が実行される。
3. 悪意のあるコントラクトのFallback関数がコールされ、意図的なエラーが発生する。（エクセプションがスローされる）
4. オークションコントラクトでエラーが発生し、bid関数のロールバック処理が行われる。

つまり、今後だれがオークションコン用トラクトへbid（入札）しても最高提示額の更新は行うことができない状態になってしまっています。

この手法を使うと、１回だけ最高提示額を提示すればそのオークションで落札することが可能になります。

次回は、このような攻撃を避けるためのオークション用コントラクトを作成していきます。

今回はオークションを攻撃するスマートコントラクトを実装していきます。

実装

オークションを攻撃するためのコードは次の通りです。

[ソースコード]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

pragma solidity ^0.4.11;
contract  EvilBidder {
    /// Fallback関数（返金時にコールされる）
    function() payable{
        revert();   // エラーを発生する(Exceptionをスローする)
    }

    /// bid用の関数
    function bid(address _to) public payable {
        // bidを行う
        if(!_to.call.value(msg.value)(bytes4(sha3("bid()")))) {
            throw;
        } 
    }
}

各関数の説明は下記のとおりです。

• Fallback関数(4行目)
  無名の関数となっていて、返金が発生した場合に呼び出されます。
• revert関数(5行目)
  意図的にエラーを発生させます。
• bid関数(9行目)
  引数で指定されたアドレス(_to)に対して送金処理を行う関数です。
  オークション用のコントラクトに対して入札を行います。
  （_toアドレスを持つコンストラクトのbid関数を、msg.valueを送金金額として呼び出す。）
  Solidityで記述された関数はコンパイルされると、関数のSHA3ハッシュ値の最初の4バイトで識別されます。

次回は、この悪意のあるコントラクトを使ってオークション用のコントラクトを攻撃していきます。

オークション用のコントラクトを実行していきます。

アカウントごとの役割

アカウントの役割は次の通りです。

• MAIN ACCOUNT (eth.accounts[0]) “0xec3b01f36b44182746ca109230567c4915512e35”
  オークションの オーナー。
• ACCOUNT1 (eth.accounts[1]) “0x63f25b9bbd974fdfa07477cb99c60d2073cfe560”
  Bidder1（入札者１）。アカウント１。
• ACCOUNT2 (eth.accounts[2]) “0xd5adf1e9fbc1ed869ed4c7372961238fddc760a5”
  Bidder2（入札者２）。アカウント２。
• ACCOUNT3 (eth.accounts[3])
  マイナー

デプロイ

まずはデプロイを行います。デプロイアカウントはMAIN ACCOUNTです。

[デプロイ時のイメージ]

デプロイ直後のコンストラクトの状態を確認します。

[コンストラクトの状態]

• コンストラクトの残高確認
  0 ether
• 最高提示者のアドレス確認
  Main account
• 最高提示額の確認
  0 wei

まだ入札されていないためコンストラクトの残高が0etherで、最高提示者がオーナーアドレス(Main account)になっています。

最初の入札

アカウント１から最初の入札を行ってみます。

入札前にアカウント１の残高確認を確認します。

[アカウント１の残高]

アカウント１からBid関数をコールして、10etherをbid(入札)します。

[最初の入札]

入札後のアカウント１の残高は次の通りです。

[アカウント１の残高]

10ether減っていることが確認できます。

最初の入札後のコンストラクトの状態を確認します。

[コンストラクトの状態]

• コンストラクトの残高確認
  10 ether
• 最高提示者のアドレス確認
  Account1
• 最高提示額の確認
  10000000000000000000 wei

アカウント１が最高提示者となり、コンストラクトの残高が10ehterに増えていることが確認できます。

２回目の入札

アカウント２から、２回目の入札を行います。

入札前のアカウント２の残高は次の通りです。

[アカウント２の残高]

アカウント２からBid関数をコールして、20etherをbid(入札)します。

[２回目の入札]

入札後のアカウント２の残高は次の通りです。

[アカウント２の残高]

20ether減っていることが確認できます。

２回目の入札後のコンストラクトの状態を確認します。

[コンストラクトの状態]

• コンストラクトの残高確認
  20 ether
• 最高提示者のアドレス確認
  Account2
• 最高提示額の確認
  20000000000000000000 wei

アカウント２が最高提示者となり、コンストラクトの残高が20ehterに増えていることが確認できます。

最初の入札者への返金確認

アカウント２が最高提示額となったため、アカウント１へ返金処理が行われているはずです。

アカウント１の残高を確認します。

[アカウント１の残高]

10etherが返金され、アカウント１の残高が入札前の状態に戻っていることが確認できました。

以上で、一通りのオークションとしての動作が確認できたことになります。

脆弱性

実はこのコンストラクトでは悪意のあるコンストラクトからの攻撃に弱いという問題があります。

次回は、悪意のあるコンストラクトを作成し、このオークション用のコンストラクトに対して攻撃を行ってみます。

今回はオークションの機能をスマートコントラクトで実装していきます。

実装

オークションを実現するためのコードは次の通りです。

[ソースコード]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

pragma solidity ^0.4.11;
contract Auction {
    address public highestBidder;   // 最高額提示アドレス
    uint public highestBid;         // 最高提示額

    /// コンストラクタ
    function Auction() payable {
        highestBidder = msg.sender;
        highestBid = 0;
    }

    /// Bid用の関数
    function bid() public payable {
        // bidが現在の最高額よりも大きいことを確認
        require(msg.value > highestBid);

        // 返金額退避
        uint refundAmount = highestBid;
        // これまで最高額を提示していたアドレス退避
        address currentHighestBidder = highestBidder;

        // ステート更新（新しい落札者を表す）
        highestBid = msg.value;
        highestBidder = msg.sender;

        // これまで最高額を提示していたbidderに返金
        if(!currentHighestBidder.send(refundAmount)) {
            throw;
        }
    }
}

このコンストラクトの仕様は次の通りです。

• 入札(bid)したいユーザは、現在の最高提示額を超えるetherの送金を伴う形でbid関数を呼び出す。
• bid関数が呼ばれると、それまで最高額を提示していたアカウントにbidしていた金額を返金する。
• 返金をするためにsend関数を使う。
  send関数は、送金対象のアドレス.send(送金額)という形式で実行する。
  送金単位はweiとなる。
• オークションとはいっても、最高額を提示している金額とアドレスを管理するだけで、締め切り期限になったら何か権利が得られる・・・といったことはやっていません🙇‍♀️

次回は、このスマートコントラクトの動作を確認していきます。

IoTで利用するスイッチを制御するコントラクトを実行していきます。

アカウントごとの役割

アカウントの役割は次の通りです。

• MAIN ACCOUNT (eth.accounts[0]) “0xec3b01f36b44182746ca109230567c4915512e35”
  オーナー
• ACCOUNT1 (eth.accounts[1]) “0x63f25b9bbd974fdfa07477cb99c60d2073cfe560”
  IoTスイッチ
• ACCOUNT2 (eth.accounts[2]) “0xd5adf1e9fbc1ed869ed4c7372961238fddc760a5”
  利用者
• ACCOUNT3 (eth.accounts[3])
  マイナー

デプロイ

まずはデプロイを行います。

デプロイアカウントはMAIN ACCOUNTで、IoTのアドレスとしてaccounts[1]のアドレスを設定します。

[デプロイ時のイメージ]

デプロイ直後のコントラクトの状態を確認します。

[デプロイ時のイメージ]

IoTステートのアドレスにAccount1が設定され、OwnerステートのアドレスにMain accountが設定されていることを確認できます。

利用登録

利用者のアドレス(Acctount 2)からpayToSwitch関数を使って、1etherを送金します。

[利用登録]

コントラクタを開いて、スイッチの状態を確認します。

[スイッチの状態確認]

支払回数(Num paid)が1となり、スイッチの状態(Switches)にAccount2が支払いをしたことや、利用できる状態であること(Status=YES)、利用終了時間(End Time)が4分後であることが確認できます。

？？？？

前回のコンストラクトの確認では、構造体の情報(ステート)がMist Walletから確認できなかったのですが、なぜか今回は確認できています。

少々困惑しておりますが、「Mist Walletでステートが確認できればそれでOK。ダメな時はgethコンソールから確認してみる」ということにしておきたいと思います。

利用ステータスの変更

利用終了時刻(利用登録から５分後)になったら、IoTスイッチ(Account 1)よりupdateStatus関数を呼び出して、statusをfalseに変更します。

[利用ステータスの変更]

変更したステータスを確認します。

[ステータスの確認]

利用状況が不可(Status=NO)になっていることが分かります。

etherの回収

利用料の1etherをオーナーアドレスから回収します。

回収前のオーナーの残高を確認しておきます。

[オーナーの残高（回収前）]

回収処理のwithdrawFunds関数を、オーナーアドレスからコールします。

[利用料の回収]

回収後のオーナーの残高を確認します。

[オーナーの残高（回収後）]

オーナーの残高が1ether増えていることが確認できました。

IoTで利用するスイッチを制御するコントラクトの動作確認は問題なく終了できました。