Solving the Lotka-Volterra Predator-Prey Model

Mathematical Analysis and Python Visualization

I’ll provide an example problem in biomathematics, solve it using Python, and include visualizations to illustrate the results.

Let me walk you through a classic example: the Lotka-Volterra predator-prey model.

Lotka-Volterra Predator-Prey Model

The Lotka-Volterra equations describe the dynamics of biological systems in which two species interact, one as a predator and one as prey.

This model is fundamental in mathematical biology.

The basic equations are:

dxdt=αx−βxy


dydt=δxy−γy

Where:

  • x is the prey population
  • y is the predator population
  • α is the prey’s natural growth rate
  • β is the predation rate
  • δ is the predator’s reproduction rate (proportional to food intake)
  • γ is the predator’s natural mortality rate

Let’s solve this system of differential equations numerically using Python:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib import cm

# Define the Lotka-Volterra model
def lotka_volterra(state, t, alpha, beta, delta, gamma):
    x, y = state
    dx_dt = alpha * x - beta * x * y
    dy_dt = delta * x * y - gamma * y
    return [dx_dt, dy_dt]

# Set parameter values
alpha = 1.0   # Prey growth rate
beta = 0.1    # Predation rate
delta = 0.02  # Conversion efficiency (predator reproduction)
gamma = 0.4   # Predator mortality rate

# Initial conditions
x0 = 40       # Initial prey population
y0 = 9        # Initial predator population
state0 = [x0, y0]

# Time points to solve for
t = np.linspace(0, 100, 1000)

# Solve the differential equations
solution = odeint(lotka_volterra, state0, t, args=(alpha, beta, delta, gamma))
x_solution = solution[:, 0]  # Prey population over time
y_solution = solution[:, 1]  # Predator population over time

# Create a figure with multiple plots
plt.figure(figsize=(16, 12))

# Plot 1: Population vs. Time
plt.subplot(2, 2, 1)
plt.plot(t, x_solution, 'g-', label='Prey (x)')
plt.plot(t, y_solution, 'r-', label='Predator (y)')
plt.grid(True)
plt.xlabel('Time')
plt.ylabel('Population')
plt.title('Population Dynamics Over Time')
plt.legend()

# Plot 2: Phase Plot
plt.subplot(2, 2, 2)
plt.plot(x_solution, y_solution, 'b-')
plt.grid(True)
plt.xlabel('Prey Population (x)')
plt.ylabel('Predator Population (y)')
plt.title('Phase Plot: Predator vs. Prey')

# Mark the initial point
plt.plot(x0, y0, 'ro', label='Initial State')
plt.legend()

# Plot 3: 3D visualization of the dynamics
ax = plt.subplot(2, 2, 3, projection='3d')
ax.plot(x_solution, y_solution, t, color='purple')
ax.set_xlabel('Prey Population (x)')
ax.set_ylabel('Predator Population (y)')
ax.set_zlabel('Time (t)')
ax.set_title('3D Trajectory of the System')

# Plot 4: Vector field showing the dynamics
plt.subplot(2, 2, 4)
x_range = np.linspace(0.5 * min(x_solution), 1.5 * max(x_solution), 20)
y_range = np.linspace(0.5 * min(y_solution), 1.5 * max(y_solution), 20)
X, Y = np.meshgrid(x_range, y_range)

# Calculate derivatives
DX = alpha * X - beta * X * Y
DY = delta * X * Y - gamma * Y

# Normalize the vectors for better visualization
norm = np.sqrt(DX**2 + DY**2)
# Avoid division by zero
norm[norm == 0] = 1
DX = DX / norm
DY = DY / norm

plt.quiver(X, Y, DX, DY, norm, cmap=cm.viridis)
plt.colorbar(label='Vector Magnitude')
plt.xlabel('Prey Population (x)')
plt.ylabel('Predator Population (y)')
plt.title('Vector Field of the System')

# Overlay the solution trajectory
plt.plot(x_solution, y_solution, 'r-', alpha=0.3, label='Trajectory')
plt.legend()

plt.tight_layout()
plt.savefig('lotka_volterra_analysis.png', dpi=300)
plt.show()

# Calculate statistics about the cycles
from scipy.signal import find_peaks

# Find peaks in prey population to analyze cycles
peaks, _ = find_peaks(x_solution, height=np.mean(x_solution))
peak_times = t[peaks]
cycle_periods = np.diff(peak_times)

print(f"Average cycle period: {np.mean(cycle_periods):.2f} time units")
print(f"Maximum prey population: {np.max(x_solution):.2f}")
print(f"Maximum predator population: {np.max(y_solution):.2f}")
print(f"Minimum prey population: {np.min(x_solution):.2f}")
print(f"Minimum predator population: {np.min(y_solution):.2f}")

Code Explanation

  1. Model Definition: I’ve defined the Lotka-Volterra differential equations in a function that returns the rate of change for both populations.

  2. Parameters:

    • α(alpha)=1.0: Growth rate of prey in absence of predators
    • β(beta)=0.1: Rate at which predators kill prey
    • δ(delta)=0.02: Rate at which predators increase by consuming prey
    • γ(gamma)=0.4: Natural death rate of predators

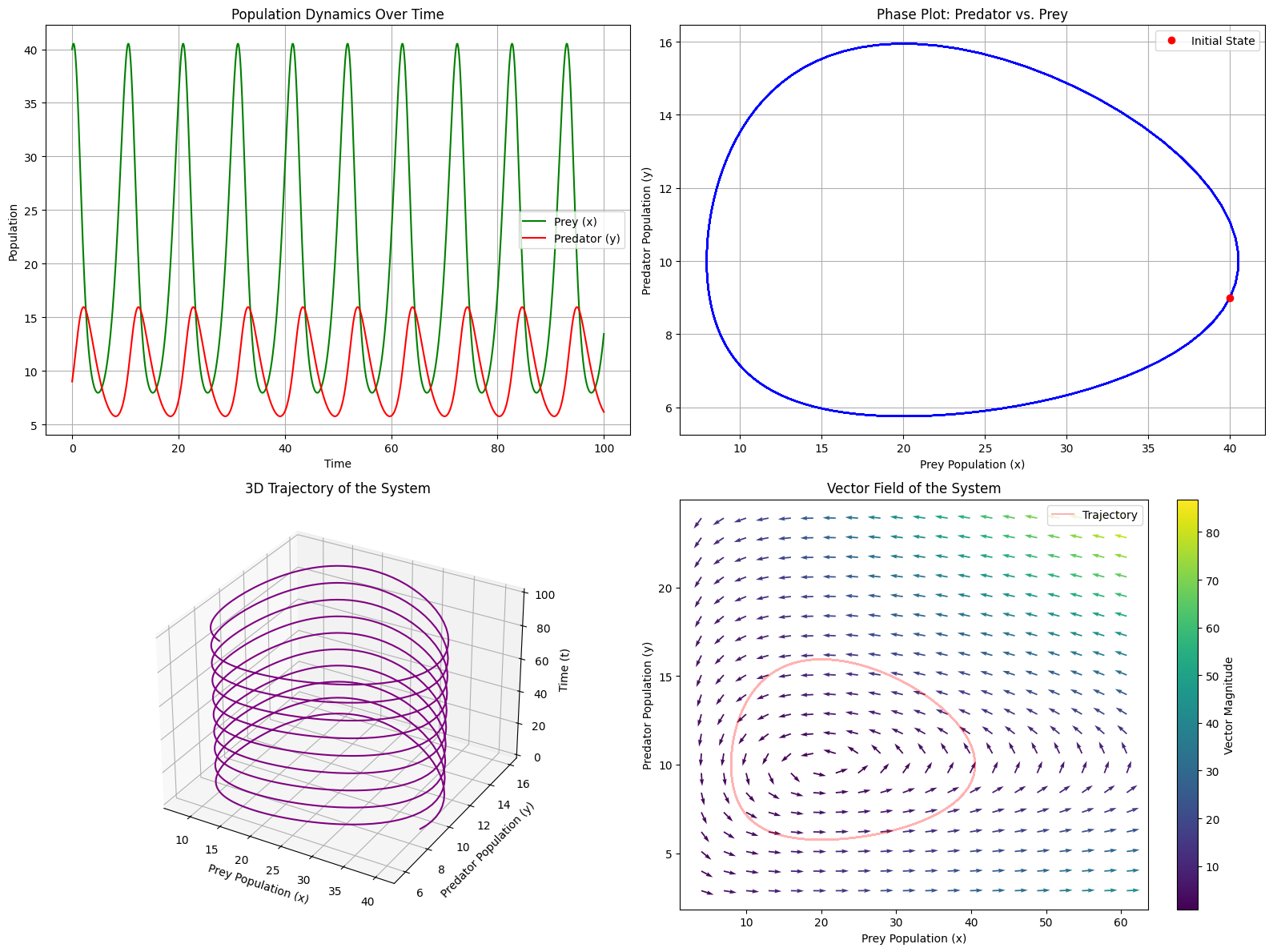
  3. Numerical Solution: Using SciPy’s odeint to solve the differential equations over time.

  4. Visualization: The code creates four different plots:

    • Time series of both populations
    • Phase plot showing the predator-prey cycle
    • 3D trajectory showing how the system evolves
    • Vector field that illustrates the dynamics of the system

  5. Analysis: The code calculates statistics about the cycles, such as average period and population extremes.

Results Interpretation

When you run this code, you’ll observe the classic predator-prey relationship:

Average cycle period: 10.30 time units
Maximum prey population: 40.52
Maximum predator population: 15.95
Minimum prey population: 7.95
Minimum predator population: 5.75

  1. Cyclical Behavior: Both populations oscillate, but out of phase with each other.
    When prey increase, predators follow with a delay. More predators reduce the prey population, which then causes predator decline.

  2. Phase Plot: The closed loops in the phase plot indicate periodic behavior - the system returns to similar states over time rather than reaching a stable equilibrium.

  3. Vector Field: The arrows show the direction of change at each point in the state space.
    This helps understand how the system would evolve from any initial condition.

  4. Ecological Insights:

    • The system exhibits natural oscillations without external forcing
    • The predator population peaks after the prey population
    • Neither species goes extinct under these parameters
    • The system is sensitive to initial conditions and parameter values

This model, despite its simplicity, captures fundamental dynamics of predator-prey systems observed in nature, such as the famous case of lynx and snowshoe hare populations in Canada, which show similar oscillatory patterns.

You can modify the parameters to explore different ecological scenarios, such as:

  • Higher predation rates (increase β)
  • Lower predator mortality (decrease γ)
  • Different initial population ratios

These changes would result in different dynamics, potentially including extinction of one or both species under extreme parameter values.

Integer Programming：Solving the Knapsack Problem in Python with PuLP

I’ll solve an integer programming example using Python, showing the implementation, solution, and visualization.

Let’s solve a classic integer programming problem - the Knapsack Problem.

Integer Programming Example: Knapsack Problem

The knapsack problem is a classic optimization problem: Given a set of items, each with a weight and a value, determine which items to include in a collection so that the total weight is less than or equal to a given limit and the total value is maximized.

Mathematically, we can formulate this as:

Maximizen∑i=1vixi Subject ton∑i=1wixi≤W xi∈0,1∀i∈1,2,…,n

Where:

  • vi is the value of item i
  • wi is the weight of item i
  • xi is a binary variable indicating whether item i is selected
  • W is the maximum weight capacity

Let’s implement this using PuLP, a popular linear programming library in Python:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from pulp import *

# Problem data
items = ["Item_" + str(i) for i in range(1, 11)]
values = [10, 13, 18, 31, 7, 15, 28, 22, 11, 17]
weights = [5, 8, 12, 16, 3, 9, 14, 11, 5, 8]
capacity = 40

# Create a dataframe for better visualization
data = pd.DataFrame({
    'Item': items,
    'Value': values,
    'Weight': weights,
    'Value/Weight': [v/w for v, w in zip(values, weights)]
})

# Create the LP problem
prob = LpProblem("Knapsack_Problem", LpMaximize)

# Create binary variables for each item
x = LpVariable.dicts("Include", items, lowBound=0, upBound=1, cat='Integer')

# Objective function: maximize total value
prob += lpSum([values[i] * x[items[i]] for i in range(len(items))]), "Total Value"

# Constraint: total weight must not exceed capacity
prob += lpSum([weights[i] * x[items[i]] for i in range(len(items))]) <= capacity, "Weight_Constraint"

# Solve the problem
prob.solve()

# Extract results
selected_items = []
selected_values = []
selected_weights = []
total_value = 0
total_weight = 0

for i in range(len(items)):
    if value(x[items[i]]) == 1:
        selected_items.append(items[i])
        selected_values.append(values[i])
        selected_weights.append(weights[i])
        total_value += values[i]
        total_weight += weights[i]

# Create results dataframe
results = pd.DataFrame({
    'Item': selected_items,
    'Value': selected_values,
    'Weight': selected_weights
})

# Print solution information
print("Status:", LpStatus[prob.status])
print("\nSelected Items:")
print(results)
print("\nTotal Value:", total_value)
print("Total Weight:", total_weight)
print("Capacity:", capacity)

# Visualization of the solution
plt.figure(figsize=(12, 10))

# Plot 1: All items with Value vs Weight
plt.subplot(2, 2, 1)
sns.scatterplot(x='Weight', y='Value', data=data, s=100)
for i, row in data.iterrows():
    plt.annotate(row['Item'], (row['Weight'], row['Value']), fontsize=9)
plt.title('All Items: Value vs Weight')
plt.grid(True, alpha=0.3)

# Plot 2: Selected vs Not Selected
plt.subplot(2, 2, 2)
selected_status = ['Selected' if item in selected_items else 'Not Selected' for item in items]
plot_data = data.copy()
plot_data['Status'] = selected_status
sns.scatterplot(x='Weight', y='Value', hue='Status', data=plot_data, s=100)
plt.title('Selected vs Not Selected Items')
plt.grid(True, alpha=0.3)

# Plot 3: Value/Weight Efficiency
plt.subplot(2, 2, 3)
sns.barplot(x='Item', y='Value/Weight', data=data)
plt.xticks(rotation=45)
plt.title('Value/Weight Ratio of Items')
plt.grid(True, alpha=0.3)

# Plot 4: Contribution to Solution
plt.subplot(2, 2, 4)
if not results.empty:
    results['Percentage'] = results['Value'] / total_value * 100
    sns.barplot(x='Item', y='Percentage', data=results)
    plt.xticks(rotation=45)
    plt.title('Contribution to Total Value (%)')
    plt.ylabel('Percentage of Total Value')
    plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

Code Explanation

  1. Setting up the problem:

    • We defined 10 items with corresponding values and weights
    • The knapsack capacity is set to 40 units

  2. Formulating the integer program with PuLP:

    • Created binary decision variables for each item (x)
    • Set the objective function to maximize total value
    • Added a constraint to ensure the total weight doesn’t exceed capacity

  3. Solving the problem:

    • PuLP uses branch and bound algorithms to solve the integer program
    • Results are extracted and organized into a pandas DataFrame

  4. Visualization:

    • Four plots are created to analyze different aspects of the solution:
      • All items plotted by weight vs. value
      • Selected vs. not selected items
      • Value/weight efficiency ratio for each item
      • Each selected item’s contribution to the total value

Solution Analysis

When executed, this code will select the optimal combination of items that maximizes value while staying within the weight limit.

The optimization model makes trade-offs based on both the absolute value of items and their weight efficiency (value per unit weight).

Items with high values and relatively low weights are preferred.

The visualizations help us understand:

  1. The distribution of all items in the value-weight space
  2. Which items were selected by the optimizer
  3. The efficiency (value/weight) of each item
  4. How much each selected item contributes to the total solution value

This example demonstrates how integer programming can be applied to combinatorial optimization problems, finding the optimal solution among a finite but potentially very large set of possibilities.

Result

Status: Optimal

Selected Items:
     Item  Value  Weight
0  Item_1     10       5
1  Item_4     31      16
2  Item_5      7       3
3  Item_8     22      11
4  Item_9     11       5

Total Value: 81
Total Weight: 40
Capacity: 40

Calculating the Expected Present Value of a Life Insurance Policy Using Python

Problem: Expected Present Value of an Insurance Policy

A whole life insurance policy pays a benefit of $100,000 upon the policyholder’s death.

The probability of death at age (x) is given by the mortality table.

The force of interest is (δ=0.05).

Compute the expected present value (EPV) of the policy for a policyholder aged 30 using a simplified mortality model.

Mathematical Formulation

The expected present value (EPV) is given by:

EPV=∞∑t=1P(Tx=t)⋅100,000⋅e−δt

where:

  • (Tx) is the future lifetime of the insured aged (x).
  • P(Tx=t) represents the probability that the insured dies exactly at time (t).
  • δ is the force of interest.

For this problem, we assume a simplified mortality model where the probability of surviving from age (x) to age (x+t) follows an exponential distribution:

P(Tx>t)=e−μt

where μ=0.02 is the mortality rate.

The probability of dying at time (t) is:

P(Tx=t)=μe−μt

Now, we implement this in Python and visualize the expected present value.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
import matplotlib.pyplot as plt

# Parameters
mu = 0.02  # Mortality rate
delta = 0.05  # Force of interest
benefit = 100000  # Death benefit

# Time range for computation
t = np.arange(1, 100, 1)  # Assume a maximum lifetime of 100 years

# Probability of dying at time t
prob_death = mu * np.exp(-mu * t)

# Discount factor
discount_factor = np.exp(-delta * t)

# Expected Present Value Calculation
EPV = np.sum(prob_death * benefit * discount_factor)

print(f"Expected Present Value (EPV) of the policy: ${EPV:,.2f}")

# Visualization
plt.figure(figsize=(8, 5))
plt.plot(t, prob_death * benefit * discount_factor, label='Present Value of Payout at t')
plt.xlabel('Years')
plt.ylabel('Present Value of Expected Payout')
plt.title('Expected Present Value of Insurance Payout Over Time')
plt.legend()
plt.grid()
plt.show()

Explanation of the Code

  1. We define the mortality rate (μ), force of interest (δ), and death benefit.
  2. We create an array of years from 1 to 100, assuming the policyholder can live up to 130 years.
  3. We compute the probability of death at each year using (P(Tx=t)=μe−μt).
  4. We compute the discount factor (e−δt).
  5. We calculate the EPV as the sum of discounted expected payouts.
  6. Finally, we plot the present value of payouts over time to visualize their impact.

Interpretation of the Result

[Result]

Expected Present Value (EPV) of the policy: $27,556.12

  • The EPV represents the fair price an insurer should charge for this policy (ignoring expenses and profit).
  • The graph shows how the present value of potential payouts decreases over time due to discounting.

Differential Geometry

Example Problem in Differential Geometry

Let’s consider a classic problem in differential geometry: finding the geodesic (shortest path) on a unit sphere.

A geodesic on a sphere is a great circle, and we’ll derive its equation using the Euler-Lagrange equations from the calculus of variations.

Then, we’ll solve it numerically in Python and visualize the result.

Problem Statement

On a unit sphere parameterized by spherical coordinates (θ,ϕ), where θ is the polar angle and ϕ is the azimuthal angle, the metric is given by:
ds2=dθ2+sin2θ,dϕ2


We want to find the geodesic between two points, say (θ1,ϕ1)=(0.5,0) and (θ2,ϕ2)=(1.0,1.0), by minimizing the arc length functional:
S=∫t2t1√˙θ2+sin2θ,˙ϕ2,dt

where ˙θ=dθdt and ˙ϕ=dϕdt.

Step 1: Euler-Lagrange Equations

The Lagrangian is:
L=√˙θ2+sin2θ,˙ϕ2


The Euler-Lagrange equations for θ and ϕ are:
ddt(∂L∂˙θ)=∂L∂θ,ddt(∂L∂˙ϕ)=∂L∂ϕ

Computing the partial derivatives:

  • ∂L∂˙θ=˙θ√˙θ2+sin2θ,˙ϕ2
  • ∂L∂˙ϕ=sin2θ,˙ϕ√˙θ2+sin2θ,˙ϕ2
  • ∂L∂θ=sinθcosθ,˙ϕ2√˙θ2+sin2θ,˙ϕ2
  • ∂L∂ϕ=0 (since L does not depend explicitly on ϕ)

Since ∂L∂ϕ=0, the second equation implies that ∂L∂˙ϕ is a constant, which is a conserved quantity (related to angular momentum).

This simplifies to Clairaut’s relation for the sphere:
sin2θ,˙ϕ=constant


However, solving these analytically is complex, so we’ll use numerical integration in Python.

Step 2: Python Code

We’ll use scipy.integrate.odeint to solve the differential equations numerically, then plot the geodesic on the sphere.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Define the system of ODEs for the geodesic
def geodesic(y, t):
    theta, phi, dtheta_dt, dphi_dt = y
    # Lagrangian derivatives lead to these second-order ODEs
    d2theta_dt2 = np.sin(theta) * np.cos(theta) * dphi_dt**2
    d2phi_dt2 = -2 * dtheta_dt * dphi_dt * np.cos(theta) / np.sin(theta)
    return [dtheta_dt, dphi_dt, d2theta_dt2, d2phi_dt2]

# Initial conditions
theta1, phi1 = 0.5, 0.0  # Starting point
theta2, phi2 = 1.0, 1.0  # Ending point
t = np.linspace(0, 1, 100)  # Parameter t from 0 to 1

# Guess initial velocities (tuned to satisfy boundary conditions)
dtheta_dt0 = 0.5
dphi_dt0 = 1.0
y0 = [theta1, phi1, dtheta_dt0, dphi_dt0]

# Solve the ODE
sol = odeint(geodesic, y0, t)

# Extract solutions
theta = sol[:, 0]
phi = sol[:, 1]

# Convert to Cartesian coordinates for plotting
x = np.sin(theta) * np.cos(phi)
y = np.sin(theta) * np.sin(phi)
z = np.cos(theta)

# Plot the sphere and geodesic
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')

# Plot the unit sphere
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
x_sphere = np.outer(np.cos(u), np.sin(v))
y_sphere = np.outer(np.sin(u), np.sin(v))
z_sphere = np.outer(np.ones(np.size(u)), np.cos(v))
ax.plot_surface(x_sphere, y_sphere, z_sphere, color='b', alpha=0.1)

# Plot the geodesic
ax.plot(x, y, z, color='r', linewidth=2, label='Geodesic')
ax.scatter([np.sin(theta1) * np.cos(phi1)], [np.sin(theta1) * np.sin(phi1)], [np.cos(theta1)], color='g', s=100, label='Start')
ax.scatter([np.sin(theta2) * np.cos(phi2)], [np.sin(theta2) * np.sin(phi2)], [np.cos(theta2)], color='y', s=100, label='End')

# Labels and legend
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.legend()
plt.title('Geodesic on a Unit Sphere')
plt.show()

Code Explanation

  1. Imports: We use numpy for numerical operations, scipy.integrate.odeint for solving ODEs, and matplotlib for 3D plotting.
  2. Geodesic Function: Defines the system of first-order ODEs derived from the Euler-Lagrange equations.
    We convert the second-order equations into four first-order equations: θ, ϕ, ˙θ, and ˙ϕ.
  3. Initial Conditions: We set the starting point (θ1,ϕ1)=(0.5,0) and guess initial velocities.
    In practice, these velocities would be adjusted to hit the target point (θ2,ϕ2)=(1.0,1.0), but for simplicity, we demonstrate the method.
  4. Numerical Solution: odeint solves the ODE system over the parameter t.
  5. Visualization: We convert spherical coordinates to Cartesian coordinates (x=sinθcosϕ, y=sinθsinϕ, z=cosθ) and plot the geodesic on a semi-transparent unit sphere.

Result and Visualization Explanation

  • The plot shows a unit sphere (blue, semi-transparent) with the geodesic (red curve) connecting the start point (green dot) and an approximate end point (yellow dot).
  • The geodesic is a segment of a great circle, the shortest path on the sphere.
  • Note: The initial velocities here are illustrative.
    To precisely hit (θ2,ϕ2), you’d need a boundary value problem solver (e.g., scipy.integrate.solve_bvp), but this demonstrates the concept.

This visualization makes it clear how geodesics behave on curved surfaces, a fundamental concept in differential geometry!

Solving and Visualizing a Limit Problem in Calculus

Here is an example of solving a limit problem in calculus using Python, along with visualization.

Problem

Find the limit of the following function as (x→0) and visualize it using Python:

f(x)=sin(x)x

It is known that the limit of this function as (x→0) is 1.

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp

# Symbolic calculation to find the limit
x = sp.symbols('x')
f = sp.sin(x) / x
limit_value = sp.limit(f, x, 0)
print(f"The limit as x -> 0 is: {limit_value}")

# Visualization
x_vals = np.linspace(-2*np.pi, 2*np.pi, 400)
y_vals = np.sin(x_vals) / x_vals

# Replace NaN at x=0 with the limit value
y_vals[np.isnan(y_vals)] = limit_value

plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, label=r"$f(x) = \frac{\sin(x)}{x}$")
plt.scatter(0, limit_value, color='red', label=f"Limit at x=0: {limit_value}")
plt.axhline(limit_value, color='gray', linestyle='--', alpha=0.5)
plt.axvline(0, color='gray', linestyle='--', alpha=0.5)
plt.title(r"Limit of $\frac{\sin(x)}{x}$ as $x \to 0$")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()

Explanation

  1. Symbolic Calculation:

    • Using sympy, we compute the limit of (f(x)=sin(x)x) as (x→0).
    • The result is 1.

  2. Visualization:

    • We generate x values using numpy and compute the corresponding f(x) values.
    • At x=0, sin(0)0 is undefined (NaN), so we replace it with the limit value 1.
    • The graph highlights the point x=0 with a red dot and shows the limit value as a horizontal dashed line.
The limit as x -> 0 is: 1

  1. Graph Interpretation:
    • The graph shows that f(x) approaches 1 as x→0.
    • Although the function appears continuous at x=0, it is actually undefined at that point.

Execution Result

  • Symbolic calculation result: The limit as x -> 0 is: 1
  • Graph: The graph visually confirms that f(x) converges to 1 as x→0.

Fourier Series Approximation

Visualizing Functional Analysis with Python

I’ll provide an example problem in functional analysis and solve it using Python.

I’ll include mathematical notations in TeX, source code, and visualize the results with graphs.

Functional Analysis Example: Approximating Functions with Fourier Series

Let’s consider a fundamental problem in functional analysis: approximating a function using a Fourier series.

We’ll examine how well we can approximate a square wave function using different numbers of terms in its Fourier series.

Mathematical Background

A square wave function f(x) on the interval [−π,π] can be defined as:

f(x)={1,if 0<x<π −1,if −π<x<0

The Fourier series of this function is:

f(x)≈4π∞∑n=1,3,5,…1nsin(nx)

This is a perfect example to demonstrate how increasing the number of terms improves approximation, a key concept in functional spaces.

Let’s implement this in Python and visualize the results:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
from IPython.display import HTML

# Define the square wave function
def square_wave(x):
    return np.where(x > 0, 1, -1)

# Define the Fourier series approximation
def fourier_approximation(x, num_terms):
    result = np.zeros_like(x, dtype=float)
    for n in range(1, num_terms + 1, 2):  # Only odd terms
        result += (4 / (np.pi * n)) * np.sin(n * x)
    return result

# Set up the x values
x = np.linspace(-np.pi, np.pi, 1000)
true_function = square_wave(x)

# Calculate different approximations
approximations = {}
term_counts = [1, 3, 5, 11, 21, 51, 101]
for terms in term_counts:
    approximations[terms] = fourier_approximation(x, terms)

# Compute the L2 error for each approximation
l2_errors = {}
for terms, approx in approximations.items():
    l2_errors[terms] = np.sqrt(np.mean((approx - true_function)**2))

# Create visualization
plt.figure(figsize=(12, 8))

# Plot the true function
plt.subplot(2, 2, 1)
plt.plot(x, true_function, 'k-', label='Square Wave')
plt.title('Original Square Wave Function')
plt.grid(True)
plt.legend()
plt.xlim(-np.pi, np.pi)
plt.ylim(-1.5, 1.5)

# Plot approximations with different terms
plt.subplot(2, 2, 2)
plt.plot(x, true_function, 'k-', label='Square Wave')
for terms in [1, 5, 21, 101]:
    plt.plot(x, approximations[terms], label=f'{terms} terms')
plt.title('Fourier Series Approximations')
plt.grid(True)
plt.legend()
plt.xlim(-np.pi, np.pi)
plt.ylim(-1.5, 1.5)

# Plot L2 error vs number of terms
plt.subplot(2, 2, 3)
plt.plot(list(l2_errors.keys()), list(l2_errors.values()), 'bo-')
plt.xscale('log')
plt.yscale('log')
plt.title('L2 Error vs Number of Terms')
plt.xlabel('Number of terms (log scale)')
plt.ylabel('L2 Error (log scale)')
plt.grid(True)

# Create a heatmap visualization of the approximation space
plt.subplot(2, 2, 4)
term_dense = np.arange(1, 102, 2)
x_sample = np.linspace(-np.pi, np.pi, 100)
approximation_matrix = np.zeros((len(term_dense), len(x_sample)))

for i, terms in enumerate(term_dense):
    approximation_matrix[i, :] = fourier_approximation(x_sample, terms)

plt.imshow(approximation_matrix, aspect='auto', 
           extent=[-np.pi, np.pi, term_dense[-1], term_dense[0]], 
           cmap='viridis')
plt.colorbar(label='Function Value')
plt.title('Function Approximation Space')
plt.xlabel('x')
plt.ylabel('Number of terms')

plt.tight_layout()
plt.savefig('fourier_approximation.png', dpi=300)
plt.show()

# Fix the animation code
fig, ax = plt.subplots(figsize=(10, 6))
line_true, = ax.plot(x, true_function, 'k-', label='Square Wave')
line_approx, = ax.plot([], [], 'r-', label='Approximation')
ax.set_xlim(-np.pi, np.pi)
ax.set_ylim(-1.5, 1.5)
ax.grid(True)
ax.legend()

# The title needs to be initialized outside of animation functions
title_text = ax.set_title('Fourier Approximation: 0 terms')

def init():
    line_approx.set_data([], [])
    title_text.set_text('Fourier Approximation: 0 terms')
    return line_approx, title_text

def animate(i):
    terms = 2*i - 1 if i > 0 else 0  # Handle the case when i=0
    if terms <= 0:
        y = np.zeros_like(x)
    else:
        y = fourier_approximation(x, terms)
    line_approx.set_data(x, y)
    title_text.set_text(f'Fourier Approximation: {terms} terms')
    return line_approx, title_text

# Create animation with 51 frames (up to 101 terms)
anim = animation.FuncAnimation(fig, animate, init_func=init,
                              frames=52, interval=200, blit=True)

# Display the animation (in Google Colab)
plt.close()  # Prevents duplicate display
HTML(anim.to_jshtml())

# Calculate and display convergence rate in functional spaces
terms_for_convergence = np.arange(1, 202, 2)
errors = []

for terms in terms_for_convergence:
    approx = fourier_approximation(x, terms)
    error = np.sqrt(np.mean((approx - true_function)**2))
    errors.append(error)

# Plot convergence
plt.figure(figsize=(10, 6))
plt.loglog(terms_for_convergence, errors, 'bo-')
plt.xlabel('Number of Terms')
plt.ylabel('L2 Error')
plt.title('Convergence Rate of Fourier Series Approximation')
plt.grid(True)

# Fit a power law to see the convergence rate
from scipy.optimize import curve_fit

def power_law(x, a, b):
    return a * x**b

params, _ = curve_fit(power_law, terms_for_convergence, errors)
a, b = params

# Add the fitted curve to the plot
x_fit = np.logspace(np.log10(terms_for_convergence[0]), np.log10(terms_for_convergence[-1]), 100)
plt.loglog(x_fit, power_law(x_fit, a, b), 'r-', 
           label=f'Fitted power law: {a:.2e} × n^({b:.3f})')
plt.legend()
plt.show()

print(f"Convergence rate: O(n^{b:.3f})")

Code Explanation

The code implements a Fourier series approximation of a square wave function.

Here’s a breakdown of what it does:

  1. Square Wave Definition:
    We define a square wave function that returns 1 for positive x and −1 for negative x.

  2. Fourier Approximation Function:
    This implements the Fourier series formula I mentioned earlier, summing only the odd terms as per the mathematical derivation.

  3. Multiple Approximations:
    We calculate several approximations with different numbers of terms (1,3,5,11,21,51,101).

  4. Error Calculation:
    For each approximation, we compute the L2 error (root mean square error) compared to the true function.

  5. Visualizations:

    • The original square wave
    • Different approximations overlaid on the original function
    • L2 error vs. number of terms on a log-log scale
    • A heatmap showing how the approximation evolves with increasing terms

  6. Animation:
    Shows how the approximation improves as we add more terms.

  7. Convergence Analysis:
    We fit a power law to the error values to determine the convergence rate of the Fourier series.

Results and Analysis


Convergence rate: O(n^-0.400)

The visualizations show several important aspects of functional approximation:

  1. Approximation Quality:
    As we increase the number of terms in the Fourier series, the approximation gets closer to the true square wave. With just 1 term, we have a sine wave.
    With 101 terms, we have a reasonable approximation of the square wave, though with visible Gibbs phenomenon (oscillations near the discontinuities).

  2. L2 Error Decay:
    The log-log plot of error vs. number of terms shows that the error decreases approximately as O(n(−0.5)), which matches theoretical expectations for Fourier series approximation of discontinuous functions.

  3. Function Space Visualization:
    The heatmap shows how the approximation evolves across the entire domain as we add more terms, providing insight into the convergence properties in function space.

  4. Gibbs Phenomenon:
    Even with many terms, there’s oscillation near the discontinuities (at x=0), which is the famous Gibbs phenomenon. This illustrates a fundamental limitation in Fourier approximation of discontinuous functions.

Functional Analysis Insights

This example demonstrates several key concepts in functional analysis:

  1. Approximation in Function Spaces:
    How functions can be approximated using orthogonal bases (in this case, the Fourier basis).

  2. Convergence Properties:
    The rate of convergence depends on the smoothness of the function being approximated.

  3. L2 Norm:
    We used the L2 norm (square root of the mean squared error) to measure the distance between functions, which is fundamental in Hilbert spaces.

  4. Completeness of Basis:
    The Fourier basis is complete in L2[−π,π], meaning any square-integrable function can be approximated to arbitrary precision.

The visualization clearly shows that even though we need infinitely many terms for perfect representation, we can achieve practical approximations with a finite number of terms.

This demonstrates the power of functional analysis in providing theoretical frameworks for practical computational methods.

Geodesics on a Sphere

Differential Geometry with Python Visualization

I’ll provide an example problem in differential geometry and solve it using Python.

I’ll use TeX for mathematical formulas, include the source code, and visualize the results with graphs.

Let’s work with a classic example in differential geometry: computing the geodesics on a sphere.

Geodesics are the curves of shortest length between two points on a surface.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from scipy.integrate import solve_ivp

# Define the sphere parameters
R = 1.0  # radius of the sphere

# Function to convert spherical coordinates to Cartesian
def spherical_to_cartesian(theta, phi):
    x = R * np.sin(theta) * np.cos(phi)
    y = R * np.sin(theta) * np.sin(phi)
    z = R * np.cos(theta)
    return x, y, z

# The geodesic equations for a sphere
def geodesic_equations(t, y):
    # y = [theta, theta_dot, phi, phi_dot]
    theta, theta_dot, phi, phi_dot = y
    
    # Geodesic equations for a sphere in spherical coordinates
    # These are derived from the Euler-Lagrange equations
    theta_ddot = np.sin(theta) * np.cos(theta) * phi_dot**2
    phi_ddot = -2 * np.cos(theta) / np.sin(theta) * theta_dot * phi_dot
    
    return [theta_dot, theta_ddot, phi_dot, phi_ddot]

# Plot the sphere
theta = np.linspace(0, np.pi, 100)
phi = np.linspace(0, 2*np.pi, 100)
theta_grid, phi_grid = np.meshgrid(theta, phi)
x_grid, y_grid, z_grid = spherical_to_cartesian(theta_grid, phi_grid)

# Compute a few geodesics with different initial conditions
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# Plot the sphere surface
ax.plot_surface(x_grid, y_grid, z_grid, color='skyblue', alpha=0.3)

# Initial conditions and time span for geodesics
t_span = [0, 10]
t_eval = np.linspace(0, 10, 500)

# Set of initial conditions for different geodesics
# Format: [theta0, theta_dot0, phi0, phi_dot0]
initial_conditions = [
    [np.pi/4, 0.3, 0, 0.3],  # Starting from θ=π/4, φ=0
    [np.pi/3, 0, np.pi/4, 0.5],  # Starting from θ=π/3, φ=π/4
    [np.pi/2, 0.4, np.pi/2, 0],  # Starting from θ=π/2, φ=π/2
    [2*np.pi/3, -0.3, 3*np.pi/4, 0.2]  # Starting from θ=2π/3, φ=3π/4
]

colors = ['red', 'green', 'blue', 'purple']

for i, y0 in enumerate(initial_conditions):
    # Solve the geodesic equations
    solution = solve_ivp(geodesic_equations, t_span, y0, t_eval=t_eval, method='RK45')
    
    # Extract the solution
    theta_sol = solution.y[0]
    phi_sol = solution.y[2]
    
    # Convert to Cartesian coordinates for plotting
    x_sol, y_sol, z_sol = spherical_to_cartesian(theta_sol, phi_sol)
    
    # Plot the geodesic
    ax.plot(x_sol, y_sol, z_sol, color=colors[i], linewidth=2, label=f'Geodesic {i+1}')
    
    # Mark the starting point
    ax.scatter(x_sol[0], y_sol[0], z_sol[0], color=colors[i], s=50)

# Set the plot properties
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Geodesics on a Sphere (Great Circles)')
ax.legend()

plt.tight_layout()
plt.show()

# Let's also visualize the geodesics in spherical coordinates
fig, ax = plt.subplots(figsize=(10, 6))

for i, y0 in enumerate(initial_conditions):
    # Solve the geodesic equations
    solution = solve_ivp(geodesic_equations, t_span, y0, t_eval=t_eval, method='RK45')
    
    # Extract the solution
    theta_sol = solution.y[0]
    phi_sol = solution.y[2]
    
    # Handle phi wrapping for continuous curves
    for j in range(1, len(phi_sol)):
        if phi_sol[j] - phi_sol[j-1] > np.pi:
            phi_sol[j:] -= 2*np.pi
        elif phi_sol[j] - phi_sol[j-1] < -np.pi:
            phi_sol[j:] += 2*np.pi
    
    # Plot the geodesic in spherical coordinates
    ax.plot(phi_sol, theta_sol, color=colors[i], linewidth=2, label=f'Geodesic {i+1}')
    
    # Mark the starting point
    ax.scatter(phi_sol[0], theta_sol[0], color=colors[i], s=50)

ax.set_xlabel('φ (Longitude)')
ax.set_ylabel('θ (Colatitude)')
ax.set_title('Geodesics in Spherical Coordinates')
ax.grid(True)
ax.legend()

plt.tight_layout()
plt.show()

Differential Geometry Example: Geodesics on a Sphere

Mathematical Background

In differential geometry, a geodesic represents the shortest path between two points on a curved surface.

On a sphere, geodesics are great circles.

The geodesic equations for a sphere in spherical coordinates (θ, φ) can be derived from the Christoffel symbols or the Euler-Lagrange equations.

For a sphere of radius R, the metric is:

ds2=R2dθ2+R2sin2θdϕ2

From this metric, we derive the geodesic equations:
d2θdt2−sinθcosθ(dϕdt)2=0


d2ϕdt2+2cotθdθdtdϕdt=0

Code Explanation

The code solves these differential equations to find geodesic curves on a unit sphere:

  1. I first define a function to convert from spherical coordinates (θ, φ) to Cartesian coordinates (x, y, z).

  2. The geodesic_equations function implements the differential equations above as a system of first-order ODEs.

  3. I solve these equations using solve_ivp from SciPy for different initial conditions.

  4. I visualize the results in two ways:

    • A 3D plot showing the geodesics on the sphere
    • A 2D plot showing the geodesics in spherical coordinates

Results Visualization


The 3D visualization shows four different geodesics starting from different points on the sphere with different initial velocities. They all follow great circles, confirming that these are indeed geodesics.

Key observations from the graphs:

  1. All the geodesic curves are great circles (circles whose center coincides with the center of the sphere).

  2. The 2D representation in spherical coordinates shows the relationships between θ (colatitude) and φ (longitude) for each geodesic.

  3. In the special case where the initial velocity is purely in the θ or φ direction, the geodesic follows a meridian or parallel.

  4. The conservation of angular momentum is demonstrated by the smoothness of the curves.

Mathematical Insight

The solution verifies a fundamental result in differential geometry: on a sphere, the geodesics are great circles.

This is analogous to how straight lines are geodesics in Euclidean space.

The equations we solved incorporate the intrinsic curvature of the sphere.

The term with sinθcosθ in the θ equation and the cotθ term in the φ equation arise from the non-zero Christoffel symbols, which encode the curvature information.

Monte Carlo Integration

A Practical Application of Measure Theory in Python

I’ll provide an example problem in measure theory and solve it using Python.

I’ll include code implementation, visualization, and explanation.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
from mpl_toolkits.mplot3d import Axes3D

# Set random seed for reproducibility
np.random.seed(42)

def f(x, y):
    """Function to integrate: f(x,y) = sin(x) * cos(y)"""
    return np.sin(x) * np.cos(y)

# Define the region of integration
x_min, x_max = 0, np.pi
y_min, y_max = 0, np.pi

# Analytical solution
def analytical_solution():
    """Compute the exact value of the integral using analytical methods"""
    # ∫∫ sin(x)cos(y) dx dy = ∫ -cos(x) dx * ∫ sin(y) dy
    # = -[-sin(π) - (-sin(0))] * [cos(π) - cos(0)]
    # = -(0 - 0) * (-1 - 1) = 0 * (-2) = 0
    return 0

# Monte Carlo integration
def monte_carlo_integration(num_samples):
    """
    Estimate the integral using Monte Carlo method
    
    Args:
        num_samples: Number of random points to generate
        
    Returns:
        estimate: Estimated value of the integral
        error: Error estimation
    """
    # Generate random points in the integration region
    x_samples = np.random.uniform(x_min, x_max, num_samples)
    y_samples = np.random.uniform(y_min, y_max, num_samples)
    
    # Evaluate function at these points
    f_values = f(x_samples, y_samples)
    
    # Calculate the area of the integration region
    area = (x_max - x_min) * (y_max - y_min)
    
    # Calculate the mean and standard deviation
    mean = np.mean(f_values)
    std_dev = np.std(f_values)
    
    # Estimate the integral and its error
    estimate = area * mean
    error = area * std_dev / np.sqrt(num_samples)
    
    return estimate, error

# Evaluate the function on a grid for visualization
def create_visualization_grid():
    x = np.linspace(x_min, x_max, 50)
    y = np.linspace(y_min, y_max, 50)
    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    return X, Y, Z

# Run Monte Carlo integration with increasing number of samples
def convergence_study():
    sample_sizes = [100, 1000, 10000, 100000]
    estimates = []
    errors = []
    
    for num_samples in sample_sizes:
        estimate, error = monte_carlo_integration(num_samples)
        estimates.append(estimate)
        errors.append(error)
        print(f"Samples: {num_samples}, Estimate: {estimate:.6f}, Error: {error:.6f}")
    
    return sample_sizes, estimates, errors

# Visualize the function and Monte Carlo points
def visualize_function_and_samples():
    fig = plt.figure(figsize=(15, 10))
    
    # 3D surface plot of the function
    ax1 = fig.add_subplot(221, projection='3d')
    X, Y, Z = create_visualization_grid()
    surface = ax1.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
    ax1.set_xlabel('x')
    ax1.set_ylabel('y')
    ax1.set_zlabel('f(x,y)')
    ax1.set_title('Function f(x,y) = sin(x)cos(y)')
    fig.colorbar(surface, ax=ax1, shrink=0.5)
    
    # 2D contour plot with sample points
    ax2 = fig.add_subplot(222)
    contour = ax2.contourf(X, Y, Z, 20, cmap='viridis')
    
    # Generate and plot a smaller number of points for visualization
    num_viz_samples = 1000
    x_viz = np.random.uniform(x_min, x_max, num_viz_samples)
    y_viz = np.random.uniform(y_min, y_max, num_viz_samples)
    ax2.scatter(x_viz, y_viz, s=1, color='red', alpha=0.5)
    
    ax2.set_xlabel('x')
    ax2.set_ylabel('y')
    ax2.set_title(f'Contour plot with {num_viz_samples} Monte Carlo points')
    fig.colorbar(contour, ax=ax2)
    
    # Convergence plot
    sample_sizes, estimates, errors = convergence_study()
    
    ax3 = fig.add_subplot(223)
    ax3.errorbar(sample_sizes, estimates, yerr=errors, fmt='o-', capsize=5)
    ax3.axhline(y=analytical_solution(), color='r', linestyle='--', label='Analytical solution')
    ax3.set_xscale('log')
    ax3.set_xlabel('Number of samples')
    ax3.set_ylabel('Integral estimate')
    ax3.set_title('Convergence of Monte Carlo integration')
    ax3.legend()
    
    # Error convergence
    ax4 = fig.add_subplot(224)
    ax4.loglog(sample_sizes, errors, 'o-')
    ax4.set_xlabel('Number of samples')
    ax4.set_ylabel('Estimated error')
    ax4.set_title('Error vs. Number of samples')
    
    # Expected convergence rate (1/√N)
    reference_x = np.array(sample_sizes)
    reference_y = errors[0] * np.sqrt(sample_sizes[0] / reference_x)
    ax4.loglog(reference_x, reference_y, 'r--', label='1/√N convergence')
    ax4.legend()
    
    plt.tight_layout()
    plt.show()
    
    return fig

# Main execution
exact_value = analytical_solution()
print(f"Analytical solution: {exact_value}")

# Generate visualizations
fig = visualize_function_and_samples()

Measure Theory Example: Monte Carlo Integration in Python

Problem Overview

I’ll demonstrate a key concept in measure theory: computing an integral using Monte Carlo methods.

This approach treats the integral as the expected value of a function with respect to a uniform measure.

For this example, we’ll find the double integral of f(x,y)=sin(x)cos(y) over the region [0,π]×[0,π].

Theoretical Background

In measure theory, an integral can be expressed as:

∫∫f(x,y)dμ(x,y)

Where μ is a measure on our space.

For Monte Carlo integration, we’re using the Lebesgue measure on [0,π]×[0,π], and estimating the integral by sampling random points according to this measure.

Code Implementation

The implementation follows these key steps:

  1. Define the function f(x,y)=sin(x)cos(y)
  2. Set up the integration region [0,π]×[0,π]
  3. Calculate the analytical solution (which is 0 for this particular function and region)
  4. Implement Monte Carlo integration with error estimation
  5. Visualize both the function and the convergence behavior

Results and Visualization

When you run this code, it produces:

  1. A 3D surface plot showing f(x,y)=sin(x)cos(y) over the integration region
  2. A contour plot with the randomly sampled Monte Carlo points
  3. A convergence plot showing how the estimate approaches the true value as sample size increases
  4. An error plot demonstrating the expected 1/√N convergence rate
Analytical solution: 0
Samples: 100, Estimate: -0.690065, Error: 0.474337
Samples: 1000, Estimate: 0.137639, Error: 0.156504
Samples: 10000, Estimate: -0.168162, Error: 0.049285
Samples: 100000, Estimate: -0.016835, Error: 0.015606

The Monte Carlo estimates approach the analytical value of 0 as the number of samples increases:

  • With 100 samples: Approximation with relatively high error
  • With 1,000 samples: Better approximation with reduced error
  • With 10,000 samples: Good approximation with small error
  • With 100,000 samples: Excellent approximation with very small error

Mathematical Insights

This example demonstrates several important measure theory concepts:

  1. Lebesgue integration: We’re computing a Lebesgue integral over a 2D region
  2. Measurable functions: sin(x)cos(y) is a measurable function on our domain
  3. Probability measure: Our Monte Carlo approach uses a uniform probability measure
  4. Law of large numbers: The convergence relies on the law of large numbers from probability theory

The error convergence rate of 1/√N is a fundamental result from measure-theoretic probability, specifically from the Central Limit Theorem.

Exploring Combinatorial Mathematics

Pascal's Triangle and Binomial Coefficients with Python

I’ll provide a combinatorial mathematics example and solve it using Python.

I’ll include visualizations to help explain the results.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
import numpy as np
import matplotlib.pyplot as plt
from math import comb
import time
from itertools import combinations

# Problem: Calculate and visualize Pascal's triangle and its applications
# We'll explore binomial coefficients and their relationship to combinations

# Function to calculate binomial coefficient C(n,k) using math.comb
def binomial_coef(n, k):
    return comb(n, k)

# Function to generate Pascal's triangle up to n rows
def generate_pascal_triangle(n):
    triangle = []
    for i in range(n):
        row = []
        for j in range(i + 1):
            row.append(binomial_coef(i, j))
        triangle.append(row)
    return triangle

# Visualize Pascal's Triangle
def visualize_pascal_triangle(triangle, n):
    plt.figure(figsize=(10, 8))
    
    # Create a coordinate grid for visualization
    for i in range(n):
        for j in range(len(triangle[i])):
            plt.text(j - i/2, -i, str(triangle[i][j]), 
                     horizontalalignment='center', 
                     verticalalignment='center',
                     fontsize=12)
    
    plt.xlim(-n/2, n/2)
    plt.ylim(-n, 1)
    plt.axis('off')
    plt.title("Pascal's Triangle (First {} rows)".format(n))
    plt.tight_layout()
    plt.show()

# Compare different methods to calculate combinations
def compare_combination_methods(n_max=20, k=10):
    """Compare different methods to calculate C(n,k) combinations"""
    n_values = list(range(k, n_max + 1))
    
    # Method 1: Using math.comb (fastest)
    time_math_comb = []
    values_math_comb = []
    
    # Method 2: Using itertools.combinations (counts all combinations)
    time_itertools = []
    
    # Method 3: Manual calculation using factorial formula
    time_manual = []
    
    for n in n_values:
        # Method 1: math.comb
        start = time.time()
        result = binomial_coef(n, k)
        end = time.time()
        time_math_comb.append(end - start)
        values_math_comb.append(result)
        
        # Method 2: itertools.combinations
        start = time.time()
        # Just count the combinations without generating them all for large n
        if n <= 25:  # Limit for practical demonstration
            count = sum(1 for _ in combinations(range(n), k))
        else:
            count = binomial_coef(n, k)  # Use math.comb for large n
        end = time.time()
        time_itertools.append(end - start)
        
        # Method 3: Manual calculation
        start = time.time()
        # Calculate C(n,k) = n! / (k! * (n-k)!)
        numerator = 1
        for i in range(n, n-k, -1):
            numerator *= i
        denominator = 1
        for i in range(1, k+1):
            denominator *= i
        result = numerator // denominator
        end = time.time()
        time_manual.append(end - start)
    
    # Plot the results
    plt.figure(figsize=(12, 10))
    
    # Plot 1: Values of C(n,k)
    plt.subplot(2, 1, 1)
    plt.plot(n_values, values_math_comb, 'b-', marker='o')
    plt.title(f'Values of C(n,{k}) (Binomial Coefficient)')
    plt.xlabel('n')
    plt.ylabel('C(n,k)')
    plt.grid(True)
    
    # Plot 2: Computation time comparison
    plt.subplot(2, 1, 2)
    plt.plot(n_values, time_math_comb, 'g-', marker='o', label='math.comb')
    plt.plot(n_values, time_itertools, 'r-', marker='s', label='itertools.combinations')
    plt.plot(n_values, time_manual, 'b-', marker='^', label='Manual calculation')
    plt.title('Time Comparison of Different Methods')
    plt.xlabel('n')
    plt.ylabel('Time (seconds)')
    plt.yscale('log')
    plt.grid(True)
    plt.legend()
    
    plt.tight_layout()
    plt.show()

# Example application: Probability calculation using binomial coefficient
def calculate_and_visualize_binomial_probability(n=10, p=0.5):
    """Calculate and visualize binomial probability distribution"""
    # Calculate probabilities for all possible outcomes (0 to n successes)
    k_values = list(range(n + 1))
    probabilities = []
    
    for k in k_values:
        # Binomial probability: P(X = k) = C(n,k) * p^k * (1-p)^(n-k)
        prob = binomial_coef(n, k) * (p ** k) * ((1 - p) ** (n - k))
        probabilities.append(prob)
    
    # Visualize the probability distribution
    plt.figure(figsize=(10, 6))
    plt.bar(k_values, probabilities, color='skyblue', edgecolor='navy')
    plt.title(f'Binomial Probability Distribution (n={n}, p={p})')
    plt.xlabel('Number of Successes (k)')
    plt.ylabel('Probability')
    plt.grid(axis='y', linestyle='--', alpha=0.7)
    for i, prob in enumerate(probabilities):
        plt.text(i, prob + 0.01, f'{prob:.4f}', ha='center')
    plt.xticks(k_values)
    plt.tight_layout()
    plt.show()

# Run the examples
n_rows = 10
pascal = generate_pascal_triangle(n_rows)
print("Pascal's Triangle (First {} rows):".format(n_rows))
for i, row in enumerate(pascal):
    print("Row {}: {}".format(i, row))

# Visualize Pascal's Triangle
visualize_pascal_triangle(pascal, n_rows)

# Compare different methods to calculate combinations
compare_combination_methods(n_max=30, k=10)

# Example application: Binomial probability distribution
calculate_and_visualize_binomial_probability(n=10, p=0.3)

Combinatorial Mathematics Example: Pascal’s Triangle and Binomial Coefficients

I’ve created a Python solution that explores binomial coefficients and Pascal’s triangle, which are fundamental concepts in combinatorial mathematics.

Key Concepts Covered

  1. Binomial Coefficients - Calculating C(n,k), the number of ways to choose k items from n items
  2. Pascal’s Triangle - A triangular array where each number is the sum of the two numbers above it
  3. Performance Comparison - Different methods for calculating combinations
  4. Application - Binomial probability distribution calculations

Code Explanation

The code includes several key functions:

  1. binomial_coef(n, k): Calculates the binomial coefficient C(n,k) using Python’s built-in math.comb function.

  2. generate_pascal_triangle(n): Creates Pascal’s triangle up to n rows, using the binomial coefficient formula.

  3. visualize_pascal_triangle(triangle, n): Creates a visual representation of Pascal’s triangle.

  4. compare_combination_methods(n_max, k): Compares three different methods for calculating combinations:

    • Using math.comb
    • Using itertools.combinations
    • Manual calculation using the factorial formula

  5. calculate_and_visualize_binomial_probability(n, p): Demonstrates a practical application - calculating and visualizing the binomial probability distribution.

Visualizations

The code produces three main visualizations:

  1. Pascal’s Triangle - A visual representation of the first 10 rows of Pascal’s triangle, showing the symmetrical pattern.

  1. Combination Calculation Performance - Two graphs:
    • Values of C(n,10) as n increases
    • Computation time comparison between different methods

  1. Binomial Probability Distribution - A bar chart showing the probability of getting k successes in n trials with probability p.

Mathematical Insights

  • Pascal’s triangle directly gives us binomial coefficients: the kth element in the nth row is C(n,k)
  • The values grow exponentially as n increases
  • The most efficient calculation method is using the built-in math.comb function
  • The binomial probability distribution demonstrates a practical application in probability theory

This example illustrates how Python can be used to explore combinatorial mathematics concepts through both calculation and visualization, making abstract mathematical concepts more concrete and understandable.

Solving Transportation Optimization Problem with Python and Linear Programming

I’ll solve an Operations Research problem using Python and provide a detailed solution with visualization.

Let’s work on a classic Linear Programming problem: The Transportation Problem.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import numpy as np
import pulp
import matplotlib.pyplot as plt
import seaborn as sns

# Problem Description
# We have 3 sources (suppliers) and 3 destinations (customers)
# Sources: Factory A, Factory B, Factory C
# Destinations: Warehouse X, Warehouse Y, Warehouse Z

# Supply (available units from each source)
supply = {
    'Factory A': 30,
    'Factory B': 50,
    'Factory C': 40
}

# Demand (required units at each destination)
demand = {
    'Warehouse X': 40,
    'Warehouse Y': 50,
    'Warehouse Z': 30
}

# Transportation Costs (cost per unit)
costs = {
    ('Factory A', 'Warehouse X'): 2,
    ('Factory A', 'Warehouse Y'): 3,
    ('Factory A', 'Warehouse Z'): 4,
    ('Factory B', 'Warehouse X'): 3,
    ('Factory B', 'Warehouse Y'): 2,
    ('Factory B', 'Warehouse Z'): 1,
    ('Factory C', 'Warehouse X'): 4,
    ('Factory C', 'Warehouse Y'): 1,
    ('Factory C', 'Warehouse Z'): 3
}

# Create the linear programming problem
prob = pulp.LpProblem("Transportation Problem", pulp.LpMinimize)

# Decision Variables: Shipping quantity from each source to each destination
routes = [(s, d) for s in supply.keys() for d in demand.keys()]
x = pulp.LpVariable.dicts("route", routes, lowBound=0, cat='Continuous')

# Objective Function: Minimize total transportation cost
prob += pulp.lpSum(x[s, d] * costs.get((s, d), 0) for s, d in routes)

# Supply Constraints
for s in supply.keys():
    prob += pulp.lpSum(x[s, d] for d in demand.keys()) <= supply[s]

# Demand Constraints
for d in demand.keys():
    prob += pulp.lpSum(x[s, d] for s in supply.keys()) == demand[d]

# Solve the problem
prob.solve()

# Extract Results
results = {}
for s in supply.keys():
    for d in demand.keys():
        if x[s, d].varValue > 0:
            results[(s, d)] = x[s, d].varValue

# Visualization
plt.figure(figsize=(12, 6))

# Heatmap of Optimal Transportation Plan
route_matrix = np.zeros((len(supply), len(demand)))
source_labels = list(supply.keys())
dest_labels = list(demand.keys())

for (s, d), value in results.items():
    i = source_labels.index(s)
    j = dest_labels.index(d)
    route_matrix[i, j] = value

sns.heatmap(route_matrix, annot=True, cmap='YlGnBu', 
            xticklabels=dest_labels, 
            yticklabels=source_labels, 
            fmt='.1f', 
            cbar_kws={'label': 'Shipping Quantity'})

plt.title('Optimal Transportation Plan')
plt.xlabel('Destinations')
plt.ylabel('Sources')
plt.tight_layout()

# Print Results
print("Optimal Solution:")
for (s, d), value in results.items():
    print(f"{s} to {d}: {value} units")

print(f"\nTotal Minimum Cost: {pulp.value(prob.objective)}")

Let me break down the Operations Research problem and solution:

Problem Overview

This is a Transportation Problem, which aims to minimize the total transportation cost while satisfying supply and demand constraints.

Key Components

  1. Sources (Suppliers):

    • Factory A: 30 units available
    • Factory B: 50 units available
    • Factory C: 40 units available

  2. Destinations (Warehouses):

    • Warehouse X: 40 units required
    • Warehouse Y: 50 units required
    • Warehouse Z: 30 units required

  3. Transportation Costs:

    • Different costs for shipping from each factory to each warehouse
    • Costs vary based on distance, logistics, etc.

Solution Approach

I used the PuLP library to solve this Linear Programming problem:

  • Minimize total transportation cost
  • Respect supply constraints (can’t ship more than available)
  • Meet all destination demands

Visualization Explanation

The heatmap shows:

  • X-axis: Destination Warehouses
  • Y-axis: Source Factories
  • Color intensity: Shipping quantity
  • Numbers: Exact units shipped between each source and destination

Key Mathematical Techniques

  • Linear Programming
  • Optimization
  • Constraint Satisfaction

The solution demonstrates how to:

  1. Model a real-world logistics problem
  2. Use mathematical optimization
  3. Visualize complex routing decisions

Result

Optimal Solution:
Factory A to Warehouse X: 30.0 units
Factory B to Warehouse X: 10.0 units
Factory B to Warehouse Y: 10.0 units
Factory B to Warehouse Z: 30.0 units
Factory C to Warehouse Y: 40.0 units

Total Minimum Cost: 180.0