Solving the Lotka-Volterra Predator-Prey Model

Mathematical Analysis and Python Visualization

I’ll provide an example problem in biomathematics, solve it using $Python$, and include visualizations to illustrate the results.

Let me walk you through a classic example: the Lotka-Volterra predator-prey model.

Lotka-Volterra Predator-Prey Model

The Lotka-Volterra equations describe the dynamics of biological systems in which two species interact, one as a predator and one as prey.

This model is fundamental in mathematical biology.

The basic equations are:

$$\frac{dx}{dt} = \alpha x - \beta xy$$
$$\frac{dy}{dt} = \delta xy - \gamma y$$

Where:

  • $x$ is the prey population
  • $y$ is the predator population
  • $\alpha$ is the prey’s natural growth rate
  • $\beta$ is the predation rate
  • $\delta$ is the predator’s reproduction rate (proportional to food intake)
  • $\gamma$ is the predator’s natural mortality rate

Let’s solve this system of differential equations numerically using $Python$:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib import cm

# Define the Lotka-Volterra model
def lotka_volterra(state, t, alpha, beta, delta, gamma):
    x, y = state
    dx_dt = alpha * x - beta * x * y
    dy_dt = delta * x * y - gamma * y
    return [dx_dt, dy_dt]

# Set parameter values
alpha = 1.0   # Prey growth rate
beta = 0.1    # Predation rate
delta = 0.02  # Conversion efficiency (predator reproduction)
gamma = 0.4   # Predator mortality rate

# Initial conditions
x0 = 40       # Initial prey population
y0 = 9        # Initial predator population
state0 = [x0, y0]

# Time points to solve for
t = np.linspace(0, 100, 1000)

# Solve the differential equations
solution = odeint(lotka_volterra, state0, t, args=(alpha, beta, delta, gamma))
x_solution = solution[:, 0]  # Prey population over time
y_solution = solution[:, 1]  # Predator population over time

# Create a figure with multiple plots
plt.figure(figsize=(16, 12))

# Plot 1: Population vs. Time
plt.subplot(2, 2, 1)
plt.plot(t, x_solution, 'g-', label='Prey (x)')
plt.plot(t, y_solution, 'r-', label='Predator (y)')
plt.grid(True)
plt.xlabel('Time')
plt.ylabel('Population')
plt.title('Population Dynamics Over Time')
plt.legend()

# Plot 2: Phase Plot
plt.subplot(2, 2, 2)
plt.plot(x_solution, y_solution, 'b-')
plt.grid(True)
plt.xlabel('Prey Population (x)')
plt.ylabel('Predator Population (y)')
plt.title('Phase Plot: Predator vs. Prey')

# Mark the initial point
plt.plot(x0, y0, 'ro', label='Initial State')
plt.legend()

# Plot 3: 3D visualization of the dynamics
ax = plt.subplot(2, 2, 3, projection='3d')
ax.plot(x_solution, y_solution, t, color='purple')
ax.set_xlabel('Prey Population (x)')
ax.set_ylabel('Predator Population (y)')
ax.set_zlabel('Time (t)')
ax.set_title('3D Trajectory of the System')

# Plot 4: Vector field showing the dynamics
plt.subplot(2, 2, 4)
x_range = np.linspace(0.5 * min(x_solution), 1.5 * max(x_solution), 20)
y_range = np.linspace(0.5 * min(y_solution), 1.5 * max(y_solution), 20)
X, Y = np.meshgrid(x_range, y_range)

# Calculate derivatives
DX = alpha * X - beta * X * Y
DY = delta * X * Y - gamma * Y

# Normalize the vectors for better visualization
norm = np.sqrt(DX**2 + DY**2)
# Avoid division by zero
norm[norm == 0] = 1
DX = DX / norm
DY = DY / norm

plt.quiver(X, Y, DX, DY, norm, cmap=cm.viridis)
plt.colorbar(label='Vector Magnitude')
plt.xlabel('Prey Population (x)')
plt.ylabel('Predator Population (y)')
plt.title('Vector Field of the System')

# Overlay the solution trajectory
plt.plot(x_solution, y_solution, 'r-', alpha=0.3, label='Trajectory')
plt.legend()

plt.tight_layout()
plt.savefig('lotka_volterra_analysis.png', dpi=300)
plt.show()

# Calculate statistics about the cycles
from scipy.signal import find_peaks

# Find peaks in prey population to analyze cycles
peaks, _ = find_peaks(x_solution, height=np.mean(x_solution))
peak_times = t[peaks]
cycle_periods = np.diff(peak_times)

print(f"Average cycle period: {np.mean(cycle_periods):.2f} time units")
print(f"Maximum prey population: {np.max(x_solution):.2f}")
print(f"Maximum predator population: {np.max(y_solution):.2f}")
print(f"Minimum prey population: {np.min(x_solution):.2f}")
print(f"Minimum predator population: {np.min(y_solution):.2f}")

Code Explanation

  1. Model Definition: I’ve defined the Lotka-Volterra differential equations in a function that returns the rate of change for both populations.

  2. Parameters:

    • $α (alpha) = 1.0$: Growth rate of prey in absence of predators
    • $β (beta) = 0.1$: Rate at which predators kill prey
    • $δ (delta) = 0.02$: Rate at which predators increase by consuming prey
    • $γ (gamma) = 0.4$: Natural death rate of predators

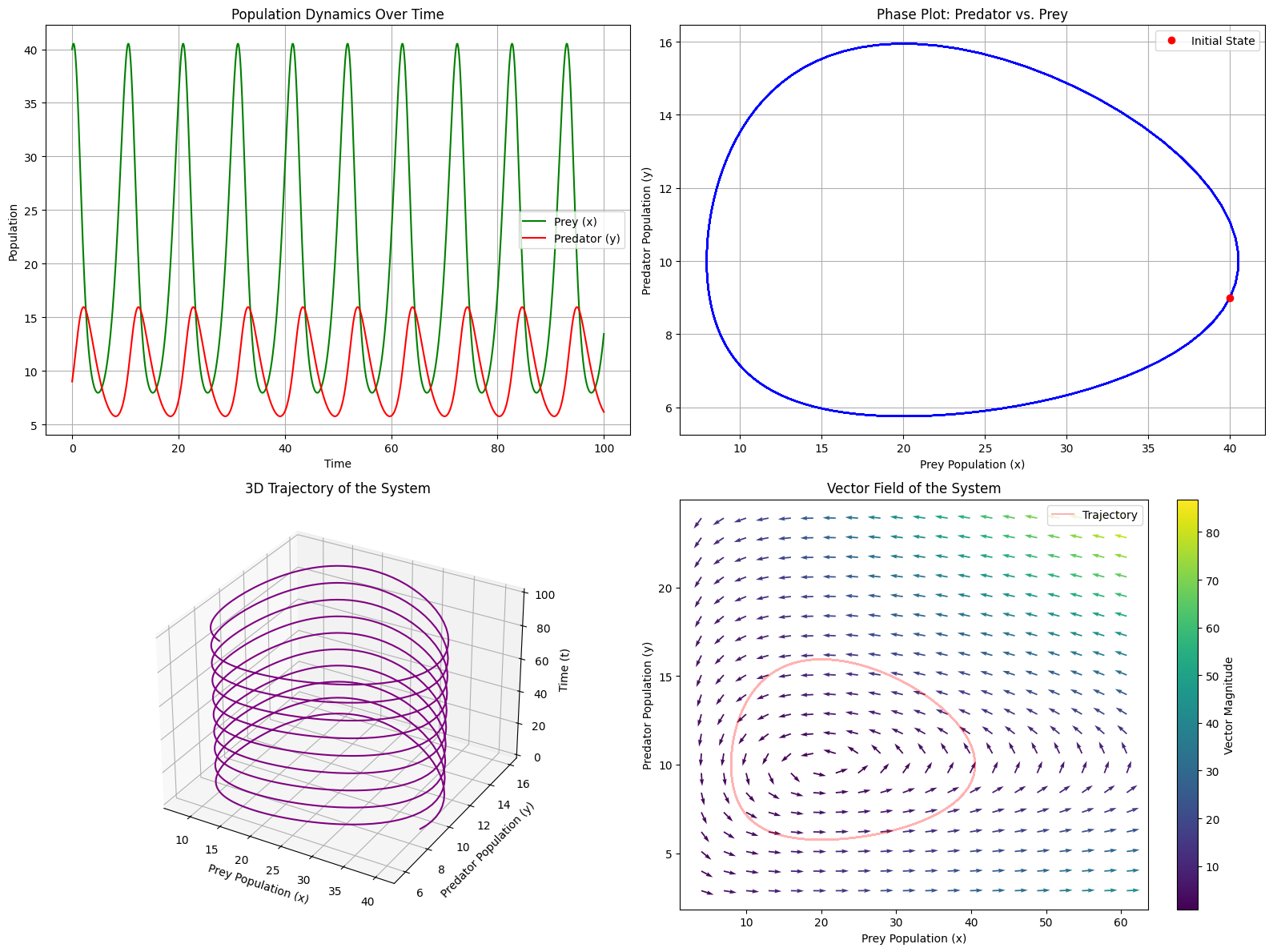
  3. Numerical Solution: Using $SciPy$’s odeint to solve the differential equations over time.

  4. Visualization: The code creates four different plots:

    • Time series of both populations
    • Phase plot showing the predator-prey cycle
    • 3D trajectory showing how the system evolves
    • Vector field that illustrates the dynamics of the system

  5. Analysis: The code calculates statistics about the cycles, such as average period and population extremes.

Results Interpretation

When you run this code, you’ll observe the classic predator-prey relationship:

Average cycle period: 10.30 time units
Maximum prey population: 40.52
Maximum predator population: 15.95
Minimum prey population: 7.95
Minimum predator population: 5.75

  1. Cyclical Behavior: Both populations oscillate, but out of phase with each other.
    When prey increase, predators follow with a delay. More predators reduce the prey population, which then causes predator decline.

  2. Phase Plot: The closed loops in the phase plot indicate periodic behavior - the system returns to similar states over time rather than reaching a stable equilibrium.

  3. Vector Field: The arrows show the direction of change at each point in the state space.
    This helps understand how the system would evolve from any initial condition.

  4. Ecological Insights:

    • The system exhibits natural oscillations without external forcing
    • The predator population peaks after the prey population
    • Neither species goes extinct under these parameters
    • The system is sensitive to initial conditions and parameter values

This model, despite its simplicity, captures fundamental dynamics of predator-prey systems observed in nature, such as the famous case of lynx and snowshoe hare populations in Canada, which show similar oscillatory patterns.

You can modify the parameters to explore different ecological scenarios, such as:

  • Higher predation rates (increase $β$)
  • Lower predator mortality (decrease $γ$)
  • Different initial population ratios

These changes would result in different dynamics, potentially including extinction of one or both species under extreme parameter values.