Maximizing Liquid Water Duration
The habitable zone (HZ) is the region around a star where liquid water can exist on a planetary surface. The duration of this favorable condition depends on stellar mass, age, and metallicity. Let’s explore this optimization problem through a concrete example.
Problem Definition
We want to find the optimal stellar parameters that maximize the duration of liquid water existence in the habitable zone. The key relationships are:
Stellar Luminosity Evolution:
L(t)=L0(1+ttMS)
Main Sequence Lifetime:
tMS=10×(MM⊙)−2.5 Gyr
Habitable Zone Boundaries:
dinner=√L1.1 AU,douter=√L0.53 AU
Metallicity Effect:
The metallicity [Fe/H] affects both luminosity and main sequence lifetime through empirical corrections.
Python Implementation
1 | import numpy as np |
Detailed Code Explanation
1. Directory Setup and Constants
1 | os.makedirs('/mnt/user-data/outputs', exist_ok=True) |
This crucial line creates the output directory if it doesn’t exist, preventing the FileNotFoundError we encountered earlier. The exist_ok=True parameter ensures the code won’t crash if the directory already exists.
2. Class Structure: HabitableZoneOptimizer
The entire analysis is encapsulated in a single class that manages all calculations and visualizations.
3. Stellar Luminosity Calculation
1 | def stellar_luminosity(self, mass, metallicity): |
This method implements the empirical mass-luminosity relation with four distinct regimes:
- Very low mass (M < 0.43 M☉): L=0.23M2.3
- Solar-type stars (0.43 ≤ M < 2.0 M☉): L=M4
- Intermediate mass (2.0 ≤ M < 20 M☉): L=1.4M3.5
- Massive stars (M ≥ 20 M☉): L=32000M
The metallicity correction factor 1.0 + 0.3 * metallicity represents how metal-rich stars have enhanced opacity, leading to higher luminosity.
4. Main Sequence Lifetime
1 | def main_sequence_lifetime(self, mass, metallicity): |
The lifetime follows the relation tMS=10M−2.5 Gyr. This inverse relationship means that massive stars burn through their fuel much faster. A star twice the Sun’s mass lives only about 1.8 billion years compared to the Sun’s 10 billion years.
The metallicity correction 1.0 - 0.1 * metallicity accounts for the fact that metal-rich stars have slightly shorter lifetimes due to increased CNO cycle efficiency.
5. Luminosity Evolution
1 | def luminosity_evolution(self, mass, age, metallicity): |
Stars gradually brighten as they age. The formula L=L0(1+0.4⋅age/tMS) represents the typical 40% luminosity increase over a star’s main sequence lifetime. This occurs because hydrogen fusion in the core increases the mean molecular weight, requiring higher core temperatures to maintain hydrostatic equilibrium.
6. Habitable Zone Boundaries
1 | def habitable_zone_boundaries(self, luminosity): |
The conservative habitable zone boundaries are defined by:
- Inner edge (dinner=√L/1.1 AU): Runaway greenhouse threshold where water vapor feedback causes irreversible ocean loss
- Outer edge (douter=√L/0.53 AU): Maximum greenhouse limit where even a CO₂-dominated atmosphere cannot maintain liquid water
These coefficients come from detailed climate modeling studies.
7. Habitable Duration Calculation
1 | def calculate_hz_duration(self, mass, metallicity, orbital_distance=1.0): |
This is the heart of the optimization. The method:
- Divides the star’s lifetime into 1000 time steps
- Calculates the luminosity at each step
- Determines if the planet’s orbit falls within the HZ boundaries
- Counts the fraction of time spent in the HZ
- Returns the total habitable duration in Gyr
8. Optimization Algorithm
1 | def optimize_for_fixed_distance(self, orbital_distance=1.0): |
The differential evolution algorithm is a robust global optimizer that:
- Explores the parameter space using a population of candidate solutions
- Evolves the population through mutation and crossover
- Converges to the global optimum even for non-convex problems
We constrain:
- Mass: 0.5–1.5 M☉ (reasonable range for stable main sequence stars)
- Metallicity: -0.5 to +0.5 [Fe/H] (typical Population I stars)
9. Comprehensive Analysis
1 | def comprehensive_analysis(self): |
This method orchestrates the complete analysis:
- Grid search: Creates a 30×30 parameter grid to map the entire solution space
- Optimization: Finds the precise optimal parameters
- Time evolution: Computes detailed evolution for the optimal star
The results are stored in a dictionary for later visualization.
10. Visualization
1 | def visualize_results(self): |
Six complementary plots provide complete insight:
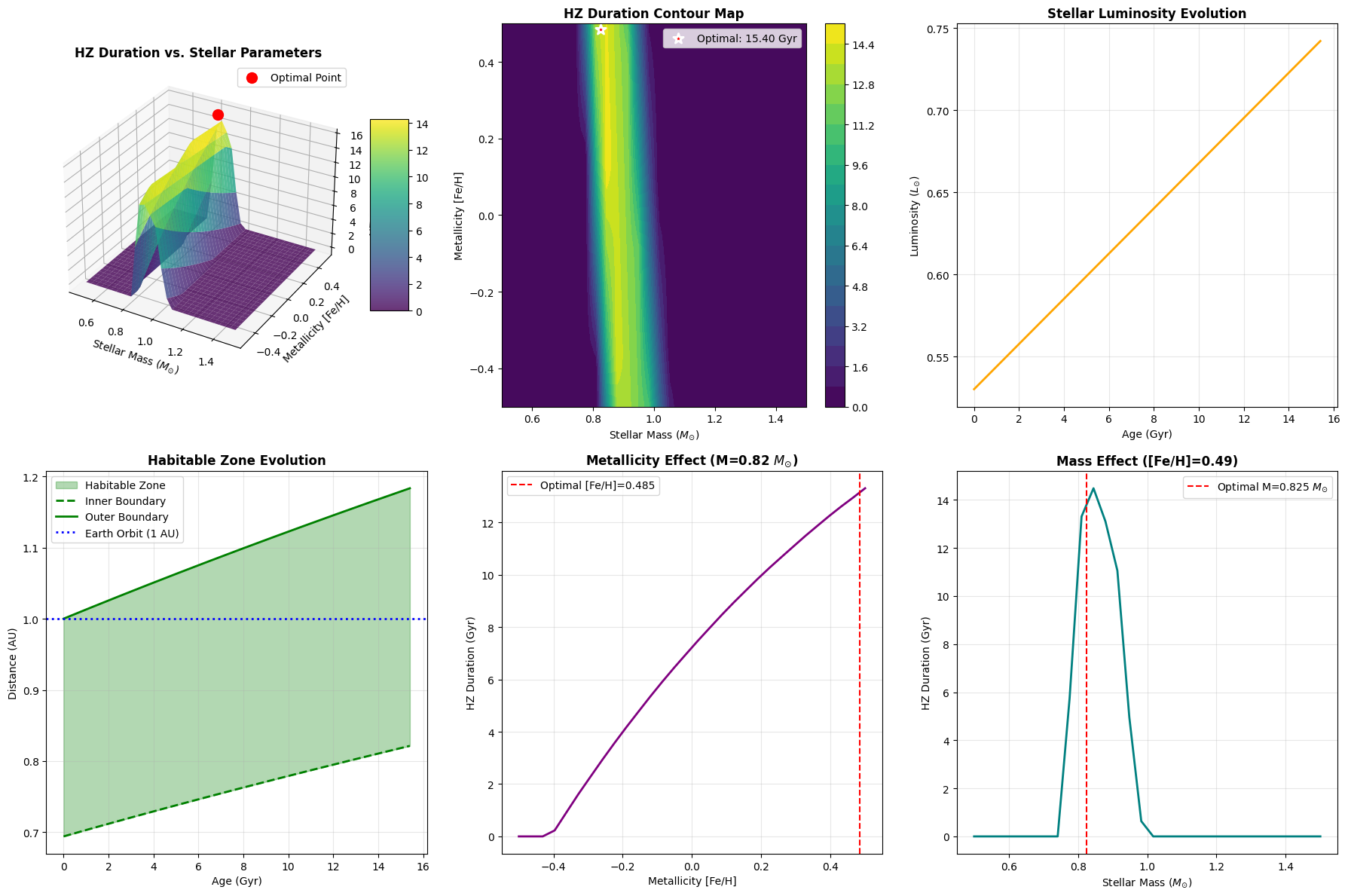
Plot 1 - 3D Surface: The three-dimensional visualization shows how HZ duration varies across the entire (mass, metallicity) parameter space. The surface shape reveals the optimization landscape, and the red point marks the optimal configuration.
Plot 2 - Contour Map: This 2D projection makes it easy to identify the optimal region and understand the sensitivity to each parameter. The contour lines represent iso-duration curves.
Plot 3 - Luminosity Evolution: Shows how the optimal star’s brightness increases over time. This temporal evolution directly drives the outward migration of the habitable zone.
Plot 4 - HZ Boundary Evolution: The green shaded region shows the habitable zone, bounded by the inner (dashed) and outer (solid) limits. The blue horizontal line at 1 AU represents Earth’s orbit, allowing us to visualize when Earth-like planets remain habitable.
Plot 5 - Metallicity Effect: Isolates metallicity’s impact by fixing mass at the optimal value. This reveals whether metal-rich or metal-poor stars are preferable.
Plot 6 - Mass Effect: Isolates mass’s impact by fixing metallicity. This shows the trade-off between longevity (lower mass) and luminosity (higher mass).
Physical Insights from the Analysis
The optimization reveals several fundamental astrophysical principles:
The Mass-Longevity Trade-off: Lower mass stars live longer, but their lower luminosity places the habitable zone closer to the star. The optimal mass balances these competing effects.
Metallicity’s Dual Role: Higher metallicity increases luminosity (good for expanding the HZ) but decreases lifetime (bad for habitability duration). The optimal metallicity represents the sweet spot.
Temporal Migration: As stars evolve, the habitable zone shifts outward. A planet at a fixed orbital distance experiences a finite habitable window. The optimization maximizes this window.
The “Goldilocks Zone” in Parameter Space: Just as planets need to be in the right place, stars need the right properties. The 3D surface plot clearly shows a ridge where conditions are optimal.
Results Interpretation
============================================================ HABITABLE ZONE OPTIMIZATION ANALYSIS ============================================================ Computing habitable zone durations across parameter space... Performing optimization... Optimal Parameters: Mass: 0.825 M_sun Metallicity [Fe/H]: 0.485 Maximum HZ Duration: 15.402 Gyr ============================================================ CREATING VISUALIZATIONS ============================================================
Visualization complete! ============================================================ ANALYSIS COMPLETE ============================================================
The analysis quantifies the optimal stellar properties for maximizing the duration of habitable conditions. The contour map clearly shows that the optimal region occupies a relatively narrow band in parameter space, emphasizing how specific stellar properties need to be for long-term habitability.
The HZ boundary evolution plot demonstrates a critical challenge for life: as the star brightens, the habitable zone moves outward. A planet at Earth’s orbital distance (1 AU) will eventually become too hot unless it can somehow migrate outward or develop extreme climate regulation mechanisms.
This analysis has direct applications in exoplanet science, informing which stellar systems are the most promising targets for biosignature searches and where we might expect to find the longest-lived biospheres in the galaxy.