行列のアダマール積

NumPyでは、ブロードキャスト の要件を満たす場合（次元数が同じ場合）、 行列の要素同士の積（アダマール積）を算出することができます。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9

import numpy as np
a = np.array([[2, 3],  # 2×2の行列を作成
              [2, 3]]
            )
b = np.array([[3, 4],  # 2×2の行列を作成
              [5, 6]]
            )

a * b                  # アダマール積を求める

[実行結果]

行列のアダマール積 を算出することができました。

行列要素同士の加算・減算

NumPy で、行列のすべての要素に対して演算を行う仕組みを ブロードキャスト と言います。

行列に対してスカラー演算を行うと、ブロードキャスト の仕組みによって全ての要素に同じ演算が適用されます。

この ブロードキャスト の仕組みを使って、行列の要素同士の足し算・引き算を行うことができます。

サンプルコード

まず２×２の行列を２つ定義して、足し算を行います。

[Google Colaboratory]

1
2
3
4
5
6
7
8

import numpy as np
a = np.array([[1, 2],   # 2×2の行列を作成
              [3, 4]]
             )
b = np.array([[4, 3],   # 2×2の行列を作成
              [2, 1]]
            )
a + b

[実行結果]

次に同じ行列を使って、引き算を行います。

[Google Colaboratory]

1

a - b

[実行結果]

行列の要素同士 で 足し算 と 引き算 を行うことができました。

行列の集計（全体）

NumPyの行列に対して、集計用の関数を使うと全ての要素が集計対象となります。

まずは、最大値を表示します。

[Google Colaboratory]

1
2
3
4
5
6
7

import numpy as np
mtx = np.array([[10, 20, 30],  # 3×3の行列を作成
                [40, 50, 60],
                [70, 80, 90]]
              )

np.max(mtx)          # 全要素の最大値

[実行結果]

次に最小値を表示します。

[Google Colaboratory]

1

np.min(mtx)          # 全要素の最小値

[実行結果]

合計値を算出します。

[Google Colaboratory]

1

np.sum(mtx)          # 全要素の合計

[実行結果]

平均を算出します。

[Google Colaboratory]

1

np.mean(mtx)         # 全要素の平均

[実行結果]

行列の全体を集計することができました。

行列の集計（部分）

行列全体ではなく、列ごとまたは行ごとに集計を行う場合は、axisオプションを使います。

axisに0 を指定すると、列ごとの集計ができます。

列ごとの合計を算出します。

[Google Colaboratory]

1

np.sum(mtx, axis=0)  # 列ごとの合計

[実行結果]

列ごとの平均を算出します。

[Google Colaboratory]

1

np.mean(mtx, axis=0) # 列ごとの平均

[実行結果]

axisに1 を指定すると、行ごとの集計ができます。

行ごとの合計を算出します。

[Google Colaboratory]

1

np.sum(mtx, axis=1) # 行ごとの合計

[実行結果]

行ごとの平均を算出します。

[Google Colaboratory]

1

np.mean(mtx, axis=1) # 行ごとの平均

[実行結果]

行列を行ごと、列ごとに集計することができました。

行列の要素にアクセス

NumPy の行列要素へのアクセスには、リストと同じようにブラケット演算子を使って次のように指定します。

　[行開始インデックス : 行終了インデックス, 列開始インデックス : 列終了インデックス]

開始インデックスは 0 から始まります。

終了インデックスは、指定したインデックスの直前までが参照されるので注意が必要です。

まずは ３×３の行列を定義しデータ型を確認します。

[Google Colaboratory]

1
2
3
4
5
6
7

# 行列の要素へのアクセス
import numpy as np
mtx = np.array([[1, 2, 3],  # 3×3の行列を作成
                [4, 5, 6],  # dtypeを指定しない場合は
                [7, 8, 9]]  # 要素の値に対応した型になる
              )
mtx.dtype       # データの型を確認

[実行結果]

次に、行列の１行目の全ての要素を表示します。（３つの指定方法があります）

[Google Colaboratory]

1

mtx[0]          # 1行目のすべての要素

[実行結果]

[Google Colaboratory]

1

mtx[0,]         # 1行目のすべての要素

[実行結果]

[Google Colaboratory]

1

mtx[0, :]       # 1行目のすべての要素

[実行結果]

行列の１列目の全ての要素を表示します。

[Google Colaboratory]

1

mtx[:, 0]       # 1列目のすべての要素

[実行結果]

２行、２列の要素を表示します。

[Google Colaboratory]

1

mtx[1, 1]       # 2行、2列の要素

[実行結果]

１行目から２行目、１列目から２列目を部分抽出します。

[Google Colaboratory]

1

mtx[0:2, 0:2]   # 1行～2行、1列～2列の部分行列を抽出

[実行結果]

いろいろなパターンで行列の要素にアクセスすることができました。

行列のスカラー演算

NumPyでは、ベクトル（配列）と同じように、行列に対して スカラー演算 を行うことができます。

ブロードキャスト によって、行列の全ての要素に対して演算が行われます。

まずは ３×３の行列 を作成します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9

import numpy as np

# 行列を作成する
import numpy as np
mtx = np.array([[1, 2, 3],         # 3×3の行列を作成
                [4, 5, 6],
                [7, 8, 9]],
               dtype = np.float)
mtx

[実行結果]

行列に対して足し算を行います。

[Google Colaboratory]

1

mtx + 10       # 足し算

[実行結果]

行列に対して引き算を行います。

[Google Colaboratory]

1

mtx - 10        # 引き算

[実行結果]

行列に対して乗算を行います。

[Google Colaboratory]

1

mtx * 2          # 乗算

[実行結果]

行列に対して除算を行います。

[Google Colaboratory]

1

mtx / 2          # 除算

[実行結果]

行列に対して剰余を算出します。

[Google Colaboratory]

1

mtx % 2          # 剰余

[実行結果]

行列に対して、各スカラー演算が行えることを確認できました。

ベクトルの内積

ベクトル同士の要素の積の和を 内積 といいます。

NumPy の ndarrayオブジェクト には、ベクトルの内積を求める dot()メソッド が用意されています。

[Google Colaboratory]

1
2
3
4
5

import numpy as np

vec1 = np.array([2, 3])
vec2 = np.array([4, 5])
np.dot(vec1, vec2)          # vec1とvec2の内積を求める

(2 × 4) + (3 × 5) の計算結果が表示されます。

[実行結果]

[Google Colaboratory]

1
2
3

vec3 = np.array([4, 5, -6])
vec4 = np.array([-2, 3, -1])
np.dot(vec3, vec4)          # vec2とvec3の内積を求める

(4 × -2) + (5 × 3) + (-6 × -1) の計算結果が表示されます。

[実行結果]

ベクトル同士の積／アダマール積

ベクトルの掛け算については、行ベクトルと列ベクトル または 列ベクトルと行ベクトル の計算が可能ですが、行ベクトル同士 または 列ベクトル同士 の掛け算はできません。

ただし ndarrayオブジェクト で表現されるベクトルは１次元配列なので、行・列の概念がありません。

足し算や引き算のように同じ次元数のベクトル同士を掛け算すると、同じ次元の成分同士が掛け算されます。

これをベクトルの アダマール積 と呼びます。

アダマール積 は、ブロードキャスト の仕組みによって実現されます。

[Google Colaboratory]

1
2
3
4
5
6

import numpy as np

vec1 = np.array([10, 20, 30])
vec2 = np.array([40, 50, 60])

vec1 * vec2     # アダマール積を求める

[実行結果]

ベクトル同士の四則演算

ベクトル同士で四則演算を行うと、同じ次元の成分同士の演算が行われます。

(ブロードキャストの仕組みによって、同じ次元の成分同士で計算されます。)

ベクトル同士の演算を行うためには、次元数が同じであることが条件となります。

次元数が異なるベクトル同士を演算すると、どちらかの成分が余ってしまうのでエラーになります。

[Google Colaboratory]

1
2
3
4
5
6

import numpy as np

vec1 = np.array([10, 20, 30])
vec2 = np.array([40, 50, 60])

vec1 + vec2                # ベクトル同士の足し算

[実行結果]

[Google Colaboratory]

1

vec1 - vec2                # ベクトル同士の引き算

[実行結果]

[Google Colaboratory]

1

vec1 / vec2                # ベクトル同士の割り算

[実行結果]

本来、ベクトル同士で割り算は行えませんが、NumPyのndarrayオブジェクトで表現するベクトルは、次元数が同じであればブロードキャストの仕組みが働いて同じ次元の成分同士で割り算が行われます。

不偏分散、不偏標準偏差

統計的推定や検定を行う場合、母集団を推定する手段として不偏分散や不偏分散から求めた不偏標準偏差が使われます。

分散はデータと平均値の差の２乗（偏差平方）の合計値（偏差平方和）をデータの個数で割って計算しますが、不偏分散は偏差平方和を データの個数－１ で割って計算します。

この場合は、var()関数やstd()関数の引数として ddof=1 を指定します。

ddof は偏差平方和を割る時の分母（データの個数）から減らす値を指定するためのオプションです。

[Google Colaboratory]

1
2
3
4
5
6

import numpy as np
x = np.array([35, 40, 45, 50, 55, 60], dtype = np.float)

# 不偏分散、不偏標準偏差を求める
print('不偏分散　　: ', np.var(x, ddof=1))
print('不偏標準偏差: ', np.std(x, ddof=1))

[実行結果]

最大値、最小値、分散、標準偏差

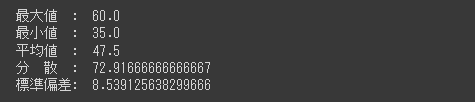
NumPyでは、最大値や最小値、平均、分散など、基本的な統計量を求める関数が用意されています。

• max()
  配列要素の最大値を返す。
• min()
  配列要素の最小値を返す。
• mean()
  配列要素の平均値を返す。
• var()
  配列要素の分散を返す。
• std()
  配列要素の標準偏差を返す。
• argmax()
  最大値の要素のインデックスを返す。
• argmin()
  最小値の要素のインデックスを返す。

[Google Colaboratory]

1
2
3
4
5
6
7
8

import numpy as np
x = np.array([35, 40, 45, 50, 55, 60], dtype = np.float)

print('最大値　: ', np.max(x))
print('最小値　: ', np.min(x))
print('平均値　: ', np.mean(x))
print('分　散　: ', np.var(x))
print('標準偏差: ', np.std(x))

[実行結果]