NetworkXを、使って 最大流問題 を解いてみます。
最大流問題
グラフ間に流れる数値を最大化させる問題を 最大流問題 といいます。
[最大流問題の例]
ネットワーク上の2台のコンピュータs、tがありsからtにデータを送ります。 このネットワークには全部でN台のコンピュータがあり、いくつかのコンピュータ間は一方向性の 通信ケーブルで接続されていて、それぞれ1秒間に通信できる最大のデータ量が決まってきます。 sからtへ1秒間で最大どれだけのデータを送信することができるでしょうか。
まず、ネットワーク上のコンピュータとデータ量をグラフに表示してみます。
[Google Colaboratory]
1 | import networkx as nx |
[実行結果]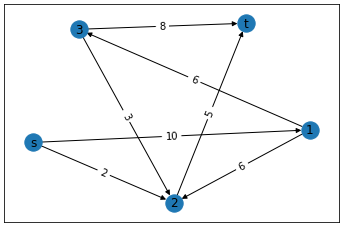
解法
最大流問題 を解くためには、maximum_flow関数 を使います。
引数には、グラフオブジェクト、始点ノード、終了ノードを設定します。
[Google Colaboratory]
1 | flow_value, flows = nx.maximum_flow(G, 's', 't') |
[実行結果]
maximum flow: 11 (s, 1): 9/10 (s, 2): 2/2 (1, 2): 3/6 (1, 3): 6/6 (3, 2): 0/3 (3, t): 6/8 (2, t): 5/5
sからtへの最大流は 11 と導き出すことができました。
また、最大流が流れる際に各ノード間に流すデータ通信も表示しています。