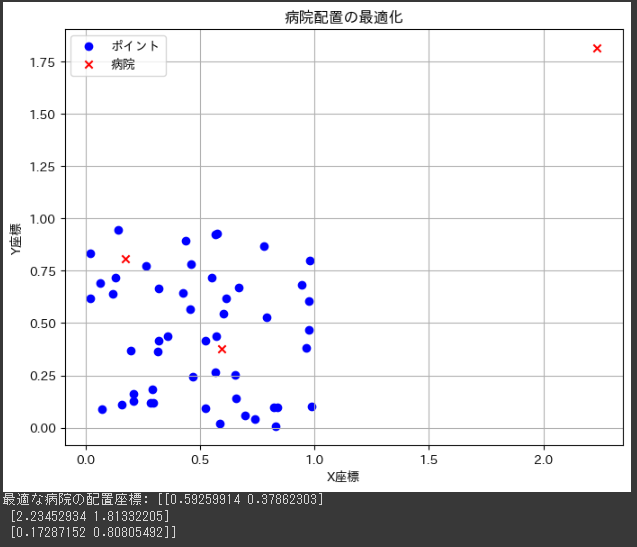
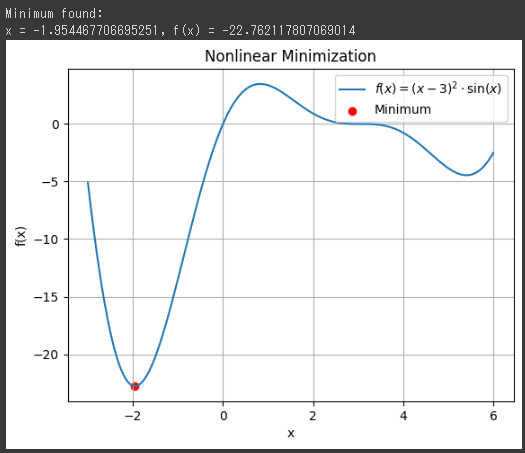
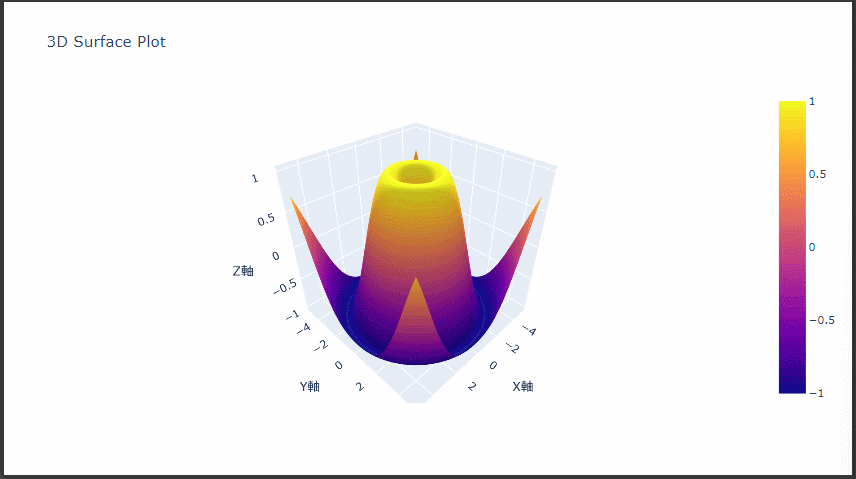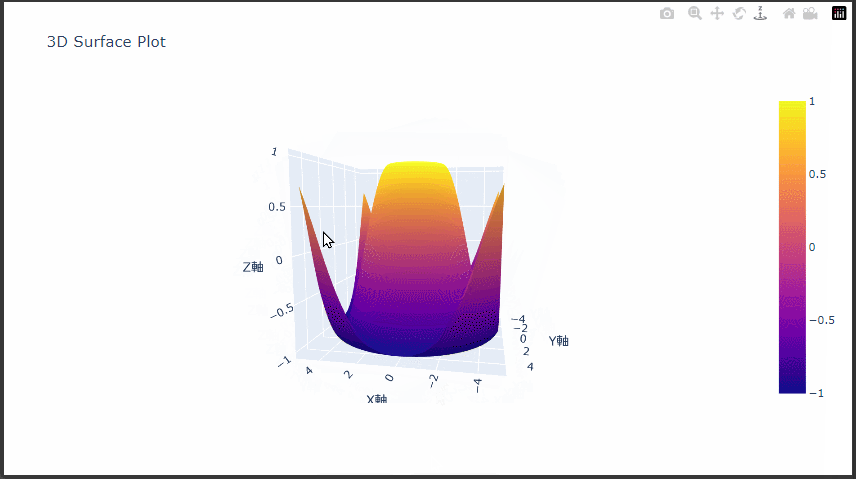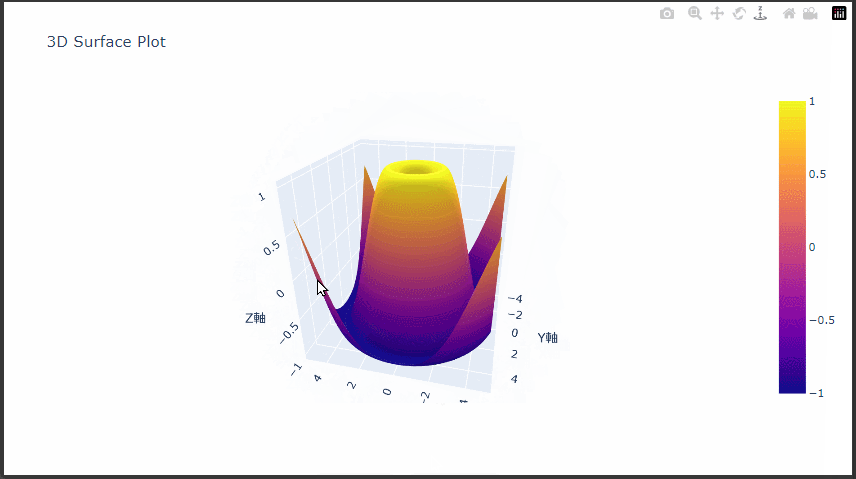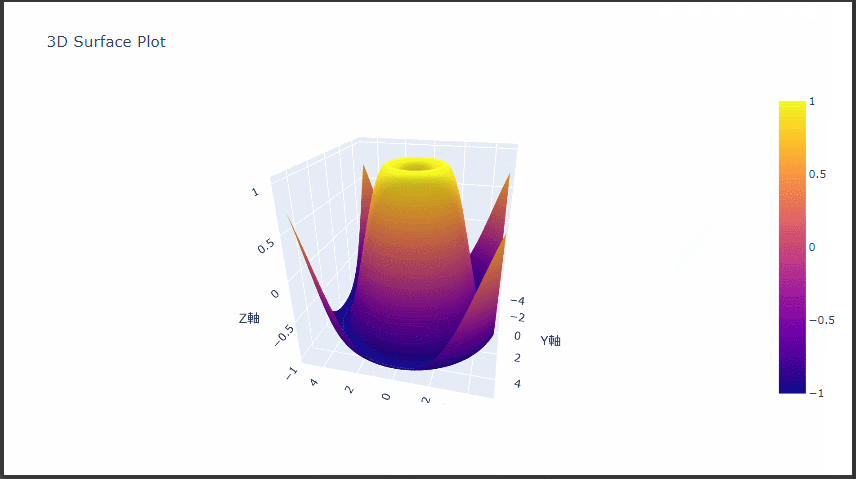
整数最適化

Pythonで整数最適化問題を解くための一般的なライブラリはPuLP、Pyomo、ortools、Gurobi、CPLEXなどがありますが、特に複雑な問題には商用のソルバーが有効です。

以下に、ortoolsを使用して整数最適化問題を解く一般的な手順を示します。

ortoolsは無料で利用でき、整数最適化問題を解くための高性能なソルバーを提供します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

from ortools.linear_solver import pywraplp

# ソルバーの初期化
solver = pywraplp.Solver.CreateSolver('SCIP')

# 変数の定義
x = solver.IntVar(0, solver.infinity(), 'x')
y = solver.IntVar(0, solver.infinity(), 'y')

# 目的関数の設定
solver.Maximize(2 * x + 3 * y)

# 制約条件の追加
solver.Add(x + 2 * y <= 8)
solver.Add(3 * x - y <= 6)

# 最適化の実行
solver.Solve()

# 結果の表示
print(f'x = {x.solution_value()}')
print(f'y = {y.solution_value()}')
print(f'最適値 = {solver.Objective().Value()}')

このコードは、整数最適化問題の基本的な例です。

制約条件と目的関数を設定し、ortoolsを使用して最適化を実行しています。

複雑な問題にはさらに多くの変数と制約を追加することができます。

[実行結果]

1
2
3

x = 2.0
y = 3.0
最適値 = 13.0

また、商用ソルバーを使用することで、より複雑な問題を解くことが可能となります。

ソースコード解説

以下はコードの詳細な説明です。

1. ortoolsから必要なモジュールをインポートします。

1

from ortools.linear_solver import pywraplp

2. ソルバーの初期化:

1

solver = pywraplp.Solver.CreateSolver('SCIP')

• CreateSolverメソッドを使用して、整数最適化ソルバーを初期化します。
  ここではSCIP（Solving Constraint Integer Programs）ソルバーを使用しています。

3. 変数の定義:

1
2

x = solver.IntVar(0, solver.infinity(), 'x')
y = solver.IntVar(0, solver.infinity(), 'y')

• IntVarメソッドを使用して整数型の変数を定義します。
  それぞれ、変数xと変数yを0以上無限大以下の整数値として定義しています。

4. 目的関数の設定:

1

solver.Maximize(2 * x + 3 * y)

• Maximizeメソッドを使用して、最大化したい目的関数を設定します。
  この例では、$2x + 3y$を最大化しようとしています。

5. 制約条件の追加:

1
2

solver.Add(x + 2 * y <= 8)
solver.Add(3 * x - y <= 6)

• Addメソッドを使用して、制約条件を追加します。
  この例では、$4x + 2y <= 8$と$3x - y <= 6$という2つの制約条件を設定しています。

6. 最適化の実行:

1

solver.Solve()

• Solveメソッドを呼び出して、整数最適化問題を解きます。

7. 結果の表示:

1
2
3

print(f'x = {x.solution_value()}')
print(f'y = {y.solution_value()}')
print(f'最適値 = {solver.Objective().Value()}')

• 最適化の結果を表示します。
  x.solution_value()とy.solution_value()はそれぞれ変数xとyの最適な値を取得し、solver.Objective().Value()は最適化された目的関数の値を取得します。

このコードは、簡単な整数最適化問題をortoolsを使用して解く方法を示しています。

実際の問題に適用する際に、目的関数と制約条件を問題に合わせて設定してください。

病院配置問題

医療に関連する最適化問題の一つとして、病院配置問題を考えてみましょう。

この問題は、病院の位置を決定し、地域内での医療サービスのアクセス性を最大化するための問題です。

ここでは、SciPyを使用して簡単な例を示し、結果を分かりやすくグラフ化します。

以下は、病院の配置を最適化するためのPythonコードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import japanize_matplotlib

# 地域内のポイント（住民や患者）の座標を生成
np.random.seed(0)
num_points = 50
points = np.random.rand(num_points, 2)

# 病院の候補地の座標を生成
num_hospitals = 3
hospital_candidates = np.random.rand(num_hospitals, 2)

# 距離関数を定義
def distance(point, hospital):
    return np.linalg.norm(point - hospital)

# 最適化問題を設定
def objective(hospital_locations):
    total_distance = 0
    for point in points:
        min_dist = min(distance(point, hospital) for hospital in hospital_locations)
        total_distance += min_dist
    return total_distance

# 初期値を設定
initial_guess = hospital_candidates.flatten()  # 1次元のベクトルに変換

# 制約条件を設定
constraints = ({'type': 'eq', 'fun': lambda x: np.array([sum(x[i] for i in range(0, len(x), 2)) - num_hospitals])},
               {'type': 'eq', 'fun': lambda x: np.array([sum(x[i] for i in range(1, len(x), 2)) - num_hospitals])})

# 最適化を実行
result = minimize(objective, initial_guess, constraints=constraints)

# 最適な病院の配置を取得
optimal_hospital_locations = result.x.reshape(-1, 2)  # 2次元の配列に変換

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.scatter(points[:, 0], points[:, 1], c='b', marker='o', label='ポイント')
plt.scatter(optimal_hospital_locations[:, 0], optimal_hospital_locations[:, 1], c='r', marker='x', label='病院')
plt.xlabel('X座標')
plt.ylabel('Y座標')
plt.title('病院配置の最適化')
plt.legend()
plt.grid(True)
plt.show()

print("最適な病院の配置座標:", optimal_hospital_locations)

このコードでは、ランダムに生成されたポイント（住民や患者）のデータと病院の候補地を使用し、ポイントと病院の距離を最小化するための最適な病院の配置を見つけます。

結果はグラフで可視化され、最適な病院の配置が表示されます。

ソースコード解説

以下はコードの詳細な説明です。

1. import ステートメント:

• numpy ライブラリ: 数値計算を行うためのPythonライブラリ。
• scipy.optimize ライブラリ: 最適化問題を解決するためのSciPyのサブモジュール。
• matplotlib.pyplot ライブラリ: グラフ描画のためのPythonライブラリ。
• japanize_matplotlib ライブラリ: Matplotlibの日本語フォントサポートを提供するためのライブラリ。

2. ポイントと病院の候補地の座標を生成:

• np.random.seed(0): 乱数生成のシードを設定して再現性を確保します。
• num_points と num_hospitals はそれぞれ、地域内のポイントと病院の候補地の数を指定します。
• points は地域内のポイントの座標をランダムに生成した2次元のNumPy配列です。
• hospital_candidates は病院の候補地の座標をランダムに生成した2次元のNumPy配列です。

3. 距離関数の定義:

• distance 関数は、2つの座標の距離を計算するための関数で、ユークリッド距離を計算しています。

4. 最適化問題の設定:

• objective 関数は、最適化問題の目標関数を定義します。
  この関数は、ポイントと病院の候補地の配置に対する総距離を最小化します。
• initial_guess は初期の病院の配置を指定します。
  最初に病院の候補地が使われますが、1次元のベクトルに変換されています。
• 制約条件 (constraints) は、病院の数が指定された数であることを確認するために設定されています。

5. 最適化を実行:

• minimize 関数は、目標関数を最小化するために最適な病院の配置を見つける最適化問題を解決します。
  初期の病院の配置と制約条件が与えられます。

6. 最適な病院の配置を取得:

• result.x から最適な病院の配置座標が取得され、2次元の配列に変換されます。

7. 結果をグラフ化:

• plt.scatter を使用して、地域内のポイント（青い点）と最適な病院の配置（赤い”X”）を2次元平面上にプロットします。
• グラフに軸ラベルやタイトルが設定されています。
• plt.show() により、グラフが表示されます。

8. 最適な病院の配置座標が表示されます。

このコードは、病院の配置問題を解決し、最適な病院の配置を可視化する例です。
医療などの実世界の問題において、リソースを最適に配置するのに役立つ最適化手法の一つを示しています。

結果解説

• 最適な病院の配置座標は、3つの病院の位置を示しています。
  それぞれの病院の配置座標は、2次元平面上の点を表します。
• 最適な配置は、与えられたポイント（青い点）と病院（赤い”X”）との距離を最小化し、ポイントができるだけ短い距離で病院にアクセスできるように配置されています。
• 3つの病院は、それぞれの配置座標で示され、地域内のポイントにサービスを提供する役割を果たします。
• グラフは、地域内のポイント（青い点）と病院（赤い”X”）を可視化し、最適な病院の配置が地域内のポイントにどのように影響を与えるかを示しています。

このような最適化問題を解決することで、医療サービスの効率的な配置が実現され、地域内の住民や患者が必要な医療ケアにアクセスしやすくなります。

非線形最小化

非線形最小化問題を示し、結果をグラフ化します。

問題: 非線形最小化

最小化する関数: $ (f(x) = (x-3)^2 \cdot \sin(x)) $

この非線形関数の最小値を見つけ、最小値に対応する $ (x) $ の値を見つけ、結果をグラフで表示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 最小化する関数
def objective_function(x):
    return (x - 3)**2 * np.sin(x)

# 初期推定値
initial_guess = [0]

# 非線形最小化を実行
result = minimize(objective_function, initial_guess, method='BFGS')

if result.success:
    print("Minimum found:")
    print(f"x = {result.x[0]}, f(x) = {result.fun}")
else:
    print("Minimum not found.")

# 関数をグラフ化
x = np.linspace(-3, 6, 400)
y = objective_function(x)

plt.plot(x, y, label='$f(x) = (x-3)^2 \cdot \sin(x)$')
plt.scatter(result.x[0], result.fun, c='red', label='Minimum')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Nonlinear Minimization')
plt.legend()
plt.grid()
plt.show()

このコードは、非線形関数 $ (f(x) = (x-3)^2 \cdot \sin(x)) $ の最小値を見つけ、最小値に対応する$ (x) $の値を見つけて、関数と最小値をグラフで表示します。

ソースコード解説

このソースコードは、SciPyを使用して非線形最小化問題を解決し、結果をグラフで視覚化するプログラムです。

以下にソースコードの詳細な説明を提供します。

1. ライブラリのインポート:

• numpy と matplotlib は数値計算とグラフ作成のために使用されます。
• scipy.optimize ライブラリから minimize 関数をインポートしています。
  この関数は最適化問題を解決するために使用されます。

2. 最小化する関数:

• objective_function(x) という関数が定義されています。
  これは非線形最小化の対象となる関数で、(f(x) = (x - 3)^2 \cdot \sin(x)) です。
  この関数の最小値を見つけることが目的です。

3. 初期推定値:

• initial_guess は初期推定値を表すリストで、この場合は ([0]) です。
  最適化アルゴリズムはこの初期値から最小値を見つけ始めます。

4. 非線形最小化の実行:

• minimize 関数が呼び出されています。
  この関数は、最小化すべき関数 objective_function と初期推定値 initial_guess を引数として受け取り、最小化を実行します。
  method='BFGS' は最適化アルゴリズムとして BFGS アルゴリズムを指定しています。

5. 結果の表示:

• result.success が True の場合、最適化アルゴリズムが収束し、最小値が見つかったことを示します。
  この場合、result.x[0] は (x) の最小値に対応する値で、result.fun は関数の最小値です。
  これらの値が表示されます。

• result.success が False の場合、最適化アルゴリズムが収束しなかったことを示します。

6. 関数のグラフ化:

• (x) の範囲を指定して、関数 (f(x)) の値を計算し、x と y に格納します。

• plt.plot を使用して、関数 (f(x)) のグラフを描画します。
  また、最小値に対応する点を plt.scatter を使用して赤い点で示します。

• グラフに x-軸と y-軸のラベルを追加し、タイトルを設定します。

• レジェンドを表示して、グリッド線を追加し、グラフを表示します。

このソースコードは、非線形最小化問題を解決し、その結果を視覚化する完全なプロセスを実行します。

結果解説

最小化の結果は次のようになりました:

• $ (x) $ の値: -1.954467706695251
• 関数の値: -22.762117807069014

この結果は、最小化された非線形関数$ (f(x) = (x-3)^2 \cdot \sin(x)) $において、最小値が求められたことを示しています。
$ (x) $の値$ -1.954467706695251$ において、関数の値は$ -22.762117807069014 $です。

これは、最適化アルゴリズムが与えられた関数に対して最小値を見つけたことを意味します。
最小値は非線形関数が最も小さな値を取る点で、この場合は$ (x \approx -1.954467706695251) $のときに$ (f(x) \approx -22.762117807069014) $になります。

最小値の位置と関数の値は、問題において最適な$ (x) $の値とそのときの目的関数の最小値を示しています。

この結果により、与えられた非線形関数の最小値が特定されました。

グラフ解説

• 関数$ (f(x) = (x-3)^2 \cdot \sin(x)) $は$、(x) $の値に対して変動する曲線です。
• グラフにはこの関数がプロットされ、最小値に対応する点が赤い点で示されています。
• グラフは x-軸と y-軸にラベルが付けられており、タイトルが付いています。
• グリッド線が表示され、関数の挙動が視覚的に確認できます。

結果とグラフは、与えられた非線形関数の最小値とその位置を示し、最適化プロセスの成功を示しています。

ローレンツアトラクター

複雑な3Dグラフの例として、カオス的なアトラクターを示すことができます。

ローレンツアトラクターはカオス的な挙動をするダイナミカルシステムの一つです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import numpy as np
import plotly.graph_objects as go

# ローレンツ方程式
def lorenz(x, y, z, s=10, r=28, b=2.667):
    x_dot = s*(y - x)
    y_dot = r*x - y - x*z
    z_dot = x*y - b*z
    return x_dot, y_dot, z_dot

# 初期条件  
x0, y0, z0 = (0., 1., 1.05)

# 軌道を計算
xs = []
ys = []
zs = []

for i in range(10000):
    x_dot, y_dot, z_dot = lorenz(x0, y0, z0)
    x0 += x_dot * 0.01
    y0 += y_dot * 0.01 
    z0 += z_dot * 0.01
    
    xs.append(x0)
    ys.append(y0) 
    zs.append(z0)
    
# 3Dプロット
fig = go.Figure(data=[go.Scatter3d(
    x=xs, y=ys, z=zs,
    mode='markers')])

fig.update_layout(
    title='Lorenz Attractor',
    width=700, height=700
)
fig.show()

ローレンツ方程式を数値的に解き、カオス的な軌道を3Dプロットします。

Plotlyを使えばこうした複雑系のシミュレーション結果も視覚的に確認できます。

ソースコード解説

以下はソースコードの詳細な説明です。

1. import numpy as np と import plotly.graph_objects as go は、NumPyとPlotlyの必要なライブラリをインポートしています。

2. def lorenz(x, y, z, s=10, r=28, b=2.667): は、ローレンツ方程式を定義する関数です。
   この方程式は、3つの微分方程式からなり、カオス的な挙動を示す非線形のダイナミカルシステムをモデル化しています。

3. x0, y0, z0 = (0., 1., 1.05) は、初期条件を指定しています。
   これらの初期条件からローレンツアトラクターの軌道が計算されます。

4. xs, ys, zs は、計算された軌道の x、y、z 座標を保存するための空のリストです。

5. ループ for i in range(10000): は、指定された回数の時間ステップにわたり、ローレンツ方程式に基づいて新しい座標を計算し、それを xs, ys, zs リストに追加します。
   このループは、ローレンツアトラクターの軌道を生成します。

6. fig は、3Dプロットを作成するためのFigureオブジェクトです。
   go.Scatter3d を使用して、計算された座標を散布図としてプロットします。

7. fig.update_layout() は、プロットの外観やレイアウトを設定します。
   タイトルとプロットのサイズを指定しています。

8. 最後の行で fig.show() を呼び出すことで、ローレンツアトラクターの3Dプロットが表示されます。

このコードはローレンツアトラクターを計算し、その軌道を3Dプロットとして可視化するためのシンプルな例です。

ローレンツアトラクターはカオス理論の一部であり、非線形ダイナミクスの重要な例です。

このプロットを実行すると、非常に複雑な3Dの軌道が表示され、カオス的な振る舞いが視覚化されます。

3Dサーフェスプロット

PythonとPlotlyを使用してインタラクティブな3Dグラフを描く例を示します。

以下の例では、3Dサーフェスプロットを作成します。

Plotlyはインタラクティブなグラフを生成するための強力なライブラリです。

まず、Plotlyをインストールします。

1

pip install plotly

次に、以下のPythonコードを使用して3Dサーフェスプロットを描きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import plotly.graph_objects as go
import numpy as np

# データを生成
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.sin(np.sqrt(x**2 + y**2))

# 3Dサーフェスプロットを作成
fig = go.Figure(data=[go.Surface(z=z, x=x, y=y)])

# グラフのレイアウトを設定
fig.update_layout(
    scene=dict(
        xaxis_title='X軸',
        yaxis_title='Y軸',
        zaxis_title='Z軸',
    ),
    title='3D Surface Plot',
)

# グラフを表示
fig.show()

このコードは、plotly.graph_objectsを使用して3Dサーフェスプロットを作成し、X軸、Y軸、Z軸にラベルを付け、タイトルを設定しています。

最後に、fig.show()でグラフを表示します。

これにより、インタラクティブな3Dグラフが表示され、ズームインや回転などの操作が可能になります。

この例は非常に基本的なものですが、Plotlyを使用してさまざまなカスタマイズとインタラクティブな機能を持つ3Dグラフを描くことができます。

データや外観を調整して、特定の要件に合わせてグラフを作成できます。

ソースコード解説

以下はソースコードの詳細な説明です。

1. plotly.graph_objectsおよびnumpyモジュールをインポートします。
   これらのモジュールは、3Dグラフの作成と数学的な計算に使用されます。

2. 3次元プロットのデータを生成します。
   xとyは-5から5までの範囲で均等に分布した100個の点から成る格子点を生成します。
   meshgrid関数は、xおよびyの格子点の行列を生成します。
   zは、xとyを使用して計算されたsin(np.sqrt(x**2 + y**2))の値から成り立ちます。
   これにより、zは3Dサーフェスプロットの高さを表す値の行列になります。

3. go.Figureを使用して3DサーフェスプロットのFigureオブジェクトを作成します。
   このFigureにはdata引数があり、サーフェスプロットのデータが含まれています。
   go.Surfaceを使用して、z値をz、x軸の値をx、y軸の値をyとしてプロットのデータを設定します。

4. fig.update_layoutを使用して、グラフの外観とレイアウトを設定します。
   scene内でxaxis_title、yaxis_title、およびzaxis_titleを設定して、各軸に対するラベルを指定します。
   また、グラフ全体のタイトルもtitleを使用して設定します。

5. 最後に、fig.show()を呼び出して、作成した3Dサーフェスプロットを表示します。
   これにより、インタラクティブなグラフが表示され、ユーザーはズームイン、回転、アニメーションなどの操作を行うことができます。

このコードは、3Dグラフの基本的な作成方法を示しており、numpyを使用して数学的な計算を行い、Plotlyを使用してグラフを描画およびカスタマイズする方法を示しています。

レベルオーダートラバーサル (Level Order Traversal) は、二分木（Binary Tree）を幅優先で探索するアルゴリズムです。

このアルゴリズムでは、木の各レベル（深さ）ごとにノードを左から右へ訪問していきます。

[探索する二分木]

1
2
3
4
5

    1
   / \
  2   3
 / \   \
4   5   6

Pythonを使って、レベルオーダートラバーサルのサンプルコードを説明します。

以下は、二分木のノードを表すクラスとレベルオーダートラバーサルを実行するコードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

class TreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None

def level_order_traversal(root):
    if not root:
        return []
    
    result = []  # レベルオーダートラバーサルの結果を格納するリスト
    queue = [root]  # キューを使用してノードを管理
    
    while queue:
        current = queue.pop(0)  # キューの先頭からノードを取り出す
        result.append(current.val)  # ノードの値を結果に追加
        
        if current.left:
            queue.append(current.left)  # 左の子ノードをキューに追加
        
        if current.right:
            queue.append(current.right)  # 右の子ノードをキューに追加
    
    return result

# 二分木の例を作成
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.right = TreeNode(6)

# レベルオーダートラバーサルを実行
result = level_order_traversal(root)

# 結果を表示
print("レベルオーダートラバーサル:", result)

このコードは、二分木をレベルオーダートラバーサルで探索する方法を示しています。

TreeNode クラスは、二分木のノードを表すために使用されます。

level_order_traversal 関数は、ルートノードから始めて幅優先でノードを訪問し、その値を result リストに追加します。

上記の例では、以下の二分木を作成し、そのレベルオーダートラバーサルの結果を表示します。

[実行結果]

1

レベルオーダートラバーサル: [1, 2, 3, 4, 5, 6]

このように、レベルオーダートラバーサルは、各レベルごとにノードを訪問するため、木の構造を保ちつつノードを効率的に探索するのに役立ちます。

ソースコード解説

このソースコードは、二分木（Binary Tree）を使って「レベルオーダートラバーサル」を行うPythonプログラムです。

レベルオーダートラバーサルは、二分木内のノードを幅優先で探索し、各レベルごとにノードの値を表示します。

以下に、ソースコードの詳細な説明を提供します。

1. TreeNode クラス:

• このクラスは、二分木のノードを表すために使用されます。
  各ノードには値 (val)、左の子ノード (left)、右の子ノード (right) が含まれます。

2. level_order_traversal 関数:

• この関数は、レベルオーダートラバーサルを実行するためのメイン関数です。
  引数としてルートノード (root) を受け取ります。
• 最初に、ルートノードが存在しない場合、空のリストを返します。
• result リストは、レベルオーダートラバーサルの結果を格納するためのリストです。
  初期化されています。
• queue リストは、ノードを管理するためにキュー（FIFO）データ構造として使用されます。
  最初にルートノードをキューに追加します。
• while ループを使用して、キューが空になるまでノードを処理します。
  • queue.pop(0) でキューの先頭からノードを取り出します。
  • 取り出したノードの値 (current.val) を result リストに追加します。
  • 左の子ノードが存在する場合、そのノードをキューに追加します。
  • 右の子ノードが存在する場合、そのノードもキューに追加します。
• すべてのノードが処理された後、result リストを返します。

3. 二分木の例の作成:

• サンプルの二分木を作成し、各ノードの値を設定しています。

4. レベルオーダートラバーサルの実行:

• level_order_traversal 関数を呼び出し、サンプルの二分木を渡してレベルオーダートラバーサルを実行します。

5. 結果の表示:

• レベルオーダートラバーサルの結果が result リストに格納されているので、それを表示します。

このプログラムは、与えられた二分木内のノードを幅優先で探索し、各レベルごとにノードの値を表示します。

数独

数独の問題を提供し、Pythonで解く方法を示します。

以下の数独の問題を解いてみましょう。

数独の問題:

1
2
3
4
5
6
7
8
9

5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9

以下は、この数独をPythonで解くためのコード例です。

このコードはバックトラッキングアルゴリズムを使用しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

def print_sudoku(board):
    for row in board:
        print(' '.join(map(str, row)))

def is_valid_move(board, row, col, num):
    # 行と列をチェック
    for i in range(9):
        if board[row][i] == num or board[i][col] == num:
            return False

    # 3x3のボックスをチェック
    start_row, start_col = 3 * (row // 3), 3 * (col // 3)
    for i in range(3):
        for j in range(3):
            if board[start_row + i][start_col + j] == num:
                return False

    return True

def solve_sudoku(board):
    for row in range(9):
        for col in range(9):
            if board[row][col] == 0:
                for num in range(1, 10):
                    if is_valid_move(board, row, col, num):
                        board[row][col] = num
                        if solve_sudoku(board):
                            return True
                        board[row][col] = 0
                return False
    return True

sudoku_board = [
    [5, 3, 0, 0, 7, 0, 0, 0, 0],
    [6, 0, 0, 1, 9, 5, 0, 0, 0],
    [0, 9, 8, 0, 0, 0, 0, 6, 0],
    [8, 0, 0, 0, 6, 0, 0, 0, 3],
    [4, 0, 0, 8, 0, 3, 0, 0, 1],
    [7, 0, 0, 0, 2, 0, 0, 0, 6],
    [0, 6, 0, 0, 0, 0, 2, 8, 0],
    [0, 0, 0, 4, 1, 9, 0, 0, 5],
    [0, 0, 0, 0, 8, 0, 0, 7, 9]
]

if solve_sudoku(sudoku_board):
    print("解決答:")
    print_sudoku(sudoku_board)
else:
    print("この数独は解けません。")

このコードは提供された数独を解き、解答を表示します。

解答は上記のコードを実行すると得られます。

[実行結果]

1
2
3
4
5
6
7
8
9
10

解決答:
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9

ソースコード解説

以下にコードの主要な部分を詳しく説明します。

1. print_sudoku(board) 関数:

• この関数は、数独の盤面を表示するために使用されます。
• board は、数独パズルの現在の状態を表す2次元のリストです。
• for row in board ループを使用して、各行を取得し、' '.join(map(str, row)) を使用して各行の数字をスペースで区切って表示します。

2. is_valid_move(board, row, col, num) 関数:

• この関数は、指定した位置 (row, col) に数字 num を配置できるかどうかを確認するために使用されます。
• 行と列が num を含んでいないこと、および3x3のボックスが num を含んでいないことを確認します。
• ボックス内の開始位置 (start_row, start_col) を計算し、そのボックス内で num が重複していないかどうかを確認します。

3. solve_sudoku(board) 関数:

• この関数は、数独パズルを解くためのメインのアルゴリズムを含みます。バックトラッキングを使用して、空のセルに適切な数字を埋めていきます。
• 各行と各列の各セルを検査し、セルが空であれば、1から9までの数字を試します。
• is_valid_move 関数を使用して、その数字がルールに適合するかどうかを確認します。
• 適切な数字が見つかれば、セルにその数字を設定し、再帰的に次のセルに進みます。
• バックトラッキングが必要な場合、セルを0にリセットして前の状態に戻ります。

4. sudoku_board:

• sudoku_board は、解くべき数独の初期状態を表す2次元リストです。空のセルは0で表現されています。

5. 最後の部分:

• solve_sudoku(sudoku_board) を呼び出し、数独パズルを解きます。
• 解が見つかった場合、解答が表示され、それが print_sudoku 関数を使用して数独の形式で表示されます。
• 解が見つからなかった場合、”この数独は解けません” と表示されます。

このコードを実行すると、与えられた数独パズルが解かれ、正しい解答が表示されるか、解答が見つからない場合には解が存在しないことが通知されます。

結果解説

数独パズルは、バックトラッキングアルゴリズムを使用して解かれました。

実行結果は以下の通りです。

[実行結果]

1
2
3
4
5
6
7
8
9

5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9

この実行結果のポイントは以下の通りです：

1. 各行と列には1から9までの数字が1回ずつ現れ、重複がありません。
2. 各3x3のボックスにも1から9までの数字が1回ずつ現れ、重複がありません。
3. 元の数独の問題に含まれていた空のセル（0）には、正しい数字が配置されています。

この解答は、数独のルールに従って正しく解かれており、数独パズルが解決されました😊

最適な教室割り当て問題

最適な教室割り当て問題は、特定の授業や講義が異なる教室で行われる場合、教室と授業の割り当てを最適化する問題です。

以下に、Pythonを使用してこの問題を簡単に解く例を示します。

この例では、教室と講義の属性を考慮して、最適な割り当てを求めます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

!pip install ortools
from ortools.linear_solver import pywraplp

# 教室の属性 (名前, 定員)
classrooms = [("A101", 30), ("B201", 40), ("C301", 50)]

# 講義の属性 (名前, 必要な教室の定員)
courses = [("Math101", 25), ("History201", 35), ("Physics301", 45)]

# 制約条件の下で最適な割り当てを見つける
def find_optimal_classroom_assignment(classrooms, courses):
    solver = pywraplp.Solver.CreateSolver('SCIP')
    if not solver:
        return

    # 教室割り当ての変数を作成
    classroom_vars = {}
    for classroom in classrooms:
        for course in courses:
            classroom_vars[(classroom, course)] = solver.IntVar(0, 1, '')

    # 各講義は正確に1つの教室に割り当てられる必要がある制約
    for course in courses:
        solver.Add(solver.Sum(classroom_vars[(classroom, course)] for classroom in classrooms) == 1)

    # 教室の定員を超えない制約
    for classroom in classrooms:
        solver.Add(solver.Sum(classroom_vars[(classroom, course)] * course[1] for course in courses) <= classroom[1])

    # 目的関数: 教室割り当ての合計数を最小化
    solver.Minimize(solver.Sum(classroom_vars[(classroom, course)] for classroom in classrooms for course in courses))

    # 最適化を解く
    solver.Solve()

    # 結果を表示
    for classroom in classrooms:
        for course in courses:
            if classroom_vars[(classroom, course)].solution_value() == 1:
                print(f"講義 '{course[0]}' は教室 '{classroom[0]}' に割り当てられました。")

find_optimal_classroom_assignment(classrooms, courses)

このコードでは、Google OR-Tools ライブラリを使用して最適な教室割り当てを求めています。

各教室と講義の属性、制約条件、および目的関数を考慮して、最適な割り当てが見つかります。

上記のコードを実行することで、講義が最適な教室に割り当てられた結果が表示されます。

[実行結果]

1
2
3

講義 'Math101' は教室 'A101' に割り当てられました。
講義 'History201' は教室 'B201' に割り当てられました。
講義 'Physics301' は教室 'C301' に割り当てられました。

ソースコード解説

以下は、このコードの詳細な説明です。

1. !pip install ortools:

まず、ortools パッケージをインストールしています。
これは、Google OR-ToolsをPythonから使用するためのパッケージです。

2. from ortools.linear_solver import pywraplp:

OR-Toolsの線形ソルバーをインポートしています。

3. classrooms と courses の定義:

教室と講義の属性をリストとして定義しています。
各教室には名前と定員が、各講義には名前と必要な教室の定員が関連付けられています。

4. find_optimal_classroom_assignment 関数:

最適な教室の割り当てを見つけるためのメイン関数です。

a. solver の作成:
SCIP（Solving Constraint Integer Programs）ソルバーを使用して、線形プログラムを解決するためのソルバーを作成します。

b. 教室割り当ての変数の作成:
教室と講義の組み合わせに対するバイナリ変数（0または1の値を取る変数）を作成します。
これらの変数は、講義を特定の教室に割り当てるかどうかを表現します。

c. 各講義は正確に1つの教室に割り当てられる必要がある制約:
各講義が正確に1つの教室に割り当てられる必要があるため、この制約を追加します。

d. 教室の定員を超えない制約:
各教室の定員を超えないようにするための制約を追加します。
講義の定員を考慮して、各講義がどの教室に割り当てられるかを決定します。

e. 目的関数:
教室割り当ての合計数を最小化するための目的関数を設定します。
つまり、割り当てられた講義の数を最小化し、余分な教室を使用しないようにします。

f. 最適化を解く:
ソルバーを使用して、制約条件の下で最適な割り当てを見つけます。

g. 結果を表示:
最適な割り当てが見つかった場合、どの講義がどの教室に割り当てられたかを表示します。

最終的に、find_optimal_classroom_assignment 関数を呼び出して、与えられた教室と講義の属性に対する最適な割り当てを見つけます。

このコードは、教育機関やスケジューリング問題など、さまざまな場面で役立つことがあります。

産業プロセスの最適化

Pythonを使用して産業プロセスの最適化を行う方法を説明します。

産業プロセス最適化は、製造、供給チェーン、エネルギー管理などさまざまな産業分野で行われており、Pythonはそのための強力なツールです。

以下に、Pythonを使用して産業プロセス最適化を行う一般的なステップを示します。

1. 問題の定義:

まず、最適化したいプロセスを明確に定義します。
目標関数、制約条件、変数などを明確にしましょう。

2. ライブラリのインポート:

Pythonでは、最適化問題を解決するための多くのライブラリが利用可能です。
代表的なものとして、SciPy、PuLP、CVXPYなどがあります。
必要に応じてこれらのライブラリをインストールし、インポートします。

3. 目標関数の設計:

目標関数を設計し、最小化または最大化したい目標を数学的に表現します。
この関数は最適化アルゴリズムの目的関数として使用されます。

4. 制約条件の設計:

制約条件を設計し、問題に適用します。
これには等式制約や不等式制約が含まれます。
制約条件はプロセスに関する物理的な制約やビジネスルールを表現します。

5. 最適化アルゴリズムの選択:

問題の性質に応じて適切な最適化アルゴリズムを選択します。
一般的なアルゴリズムには勾配降下法、線形計画法、整数計画法などがあります。

6. 最適化の実行:

選択したアルゴリズムを使用して最適化問題を解きます。
ライブラリによって使用方法が異なりますが、通常は目標関数と制約条件を提供して問題を解決します。

7. 結果の解釈:

最適化の結果を評価し、ビジネスプロセスに適用できる形で解釈します。
最適化されたパラメータや変数の値を分析し、意思決定に活かします。

サンプル

以下はPythonを使用して産業プロセス最適化を行う例の簡単なコードです。

この例では、SciPyライブラリを使用して非線形最適化問題を解いています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

from scipy.optimize import minimize

# 目標関数を定義
def objective_function(x):
    return x[0] * x[1] * x[2]

# 初期推定値
initial_guess = [1, 1, 1]

# 制約条件を設定
constraints = ({'type': 'eq', 'fun': lambda x: x[0] * x[1] * x[2] - 4})

# 最適化を実行
result = minimize(objective_function, initial_guess, constraints=constraints)

# 結果を表示
print("最適解:", result.x)
print("最小値:", result.fun)

このコードは非常に単純な例ですが、実際のプロセス最適化にはより複雑な問題やアルゴリズムが必要となるでしょう。

問題の複雑さに応じて、適切な最適化手法を選択し、プロセスを最適化していきます。

[実行結果]

1
2

最適解: [1.58726533 1.58726533 1.58726533]
最小値: 3.9989740620270866

ソースコード解説

以下は、ソースコードの詳細な説明です：

1. from scipy.optimize import minimize：

scipyライブラリからminimize関数をインポートしています。
この関数は、最適化問題を解決するのに使用されます。

2. def objective_function(x):：

objective_functionという関数を定義しています。
これは最小化したい目標関数です。
この関数は引数 x を取り、x[0] * x[1] * x[2] を返します。
この関数を最小化することで、x の最適な値を見つけます。

3. initial_guess = [1, 1, 1]：

変数 x の初期推定値を設定しています。
これは最適化アルゴリズムのスタート地点として使用されます。

4. constraints = ({'type': 'eq', 'fun': lambda x: x[0] * x[1] * x[2] - 4})：

制約条件を設定しています。
この例では、x[0] * x[1] * x[2] - 4 がゼロであるという等式制約を設定しています。
つまり、最適解はこの等式を満たす必要があります。

5. result = minimize(objective_function, initial_guess, constraints=constraints)：

minimize関数を使用して最適化を実行します。
目標関数 objective_function、初期推定値 initial_guess、および制約条件 constraints を指定します。
この関数は最適解を見つけ、その結果をresult変数に格納します。

6. print("最適解:", result.x)：

最適解（変数 x の最適な値）を表示します。

7. print("最小値:", result.fun)：

目標関数の最小値を表示します。
この値は最適解での目標関数の値です。

簡単に言えば、このコードは目標関数を最小化するための変数 x の最適な値を見つけるために、初期推定値と制約条件を使用して数値最適化を実行しています。

この例では、3つの変数を持つ目標関数を扱い、特定の等式制約を満たす最適解を見つけることを試みています。

結果解説

[実行結果]

1
2

最適解: [1.58726533 1.58726533 1.58726533]
最小値: 3.9989740620270866

実行結果について詳しく説明します：

1. 最適解: [1.58726533 1.58726533 1.58726533]：

これは、最適化アルゴリズムによって見つかった目的関数を最小化するための変数 x の値です。
具体的には、変数 x の各要素が [1.58726533, 1.58726533, 1.58726533] です。
この値は、目標関数 x[0] * x[1] * x[2] を最小化するための最適な x の値を表します。
これにより、目的関数の値が最小化されることが示唆されます。

2. 最小値: 3.9989740620270866：

これは、目標関数が最適解での値です。
最適解での変数 x の値 [1.58726533, 1.58726533, 1.58726533] を目標関数 x[0] * x[1] * x[2] に代入した結果です。
つまり、この値 3.9989740620270866 は、最適解での目標関数の最小値を表します。

総括すると、提供された結果は、指定された目標関数と制約条件に基づいて、最適化アルゴリズムによって見つかった最適解の変数値と、その最適解での目標関数の値を示しています。

最適解では、目標関数の値が 3.9989740620270866 になり、変数 x の値が [1.58726533, 1.58726533, 1.58726533] になります。

制約充足問題（CSP）を解決するためには、専門的な制約充足プログラム（CSP）ソルバーやライブラリを使用することが一般的です。

PythonでCSPを解決するための有名なライブラリの一つはpython-constraintです。

以下に、python-constraintを使用してCSPを解決し、結果を分かりやすくグラフ化する例を示します。

まず、python-constraintをインストールします:

1

pip install python-constraint

次に、CSPを解決する例を示します。

以下の例では、4つの変数（A、B、C、D）に対する制約を設定し、CSPソルバーを使用して解を見つけます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

from constraint import *

# CSP問題のインスタンスを作成
problem = Problem()

# 変数を定義
problem.addVariable("A", [1, 2, 3])
problem.addVariable("B", [1, 2, 3])
problem.addVariable("C", [1, 2, 3])
problem.addVariable("D", [1, 2, 3])

# 制約を追加
def custom_constraint(a, b, c, d):
    # 例の簡単な制約：A + B == C * D
    return a + b == c * d

problem.addConstraint(custom_constraint, "ABCD")

# CSP問題を解く
solutions = problem.getSolutions()

# 結果を表示
for solution in solutions:
    print(solution)

このコードでは、4つの変数とそれらに適用される制約を定義しています。

次に、problem.getSolutions()を呼び出すことで、CSPの解を取得できます。

[実行結果]

1
2
3
4
5
6
7
8
9
10
11

{'A': 3, 'B': 3, 'C': 3, 'D': 2}
{'A': 3, 'B': 3, 'C': 2, 'D': 3}
{'A': 3, 'B': 1, 'C': 2, 'D': 2}
{'A': 2, 'B': 2, 'C': 2, 'D': 2}
{'A': 2, 'B': 1, 'C': 3, 'D': 1}
{'A': 2, 'B': 1, 'C': 1, 'D': 3}
{'A': 1, 'B': 3, 'C': 2, 'D': 2}
{'A': 1, 'B': 2, 'C': 3, 'D': 1}
{'A': 1, 'B': 2, 'C': 1, 'D': 3}
{'A': 1, 'B': 1, 'C': 2, 'D': 1}
{'A': 1, 'B': 1, 'C': 1, 'D': 2}

結果解説

上記の実行結果は、制約充足問題（CSP）の解のセットを表しています。

各解は変数A、B、C、およびDに対する値の組み合わせです。

例の簡単な制約 A + B == C * D を持つCSPを考えています。

以下は各解の詳細な説明です：

1. {'A': 3, 'B': 3, 'C': 3, 'D': 2}:

   • A=3, B=3, C=3, D=2の組み合わせは制約を満たします。3 + 3 == 3 * 2 は成り立ちます。

2. {'A': 3, 'B': 3, 'C': 2, 'D': 3}:

   • A=3, B=3, C=2, D=3の組み合わせも制約を満たします。3 + 3 == 2 * 3 は成り立ちます。

3. {'A': 3, 'B': 1, 'C': 2, 'D': 2}:

   • この組み合わせも制約を満たします。3 + 1 == 2 * 2 は成り立ちます。

4. {'A': 2, 'B': 2, 'C': 2, 'D': 2}:

   • A、B、C、およびDがすべて2の場合、制約は満たされます。2 + 2 == 2 * 2 は成り立ちます。

5. {'A': 2, 'B': 1, 'C': 3, 'D': 1}:

   • この組み合わせも制約を満たします。2 + 1 == 3 * 1 は成り立ちます。

6. {'A': 2, 'B': 1, 'C': 1, 'D': 3}:

   • 別の組み合わせで制約が満たされます。2 + 1 == 1 * 3 は成り立ちます。

7. {'A': 1, 'B': 3, 'C': 2, 'D': 2}:

   • A=1, B=3, C=2, D=2の組み合わせも制約を満たします。1 + 3 == 2 * 2 は成り立ちます。

8. {'A': 1, 'B': 2, 'C': 3, 'D': 1}:

   • この組み合わせも制約を満たします。1 + 2 == 3 * 1 は成り立ちます。

9. {'A': 1, 'B': 2, 'C': 1, 'D': 3}:

   • 別の組み合わせで制約が満たされます。1 + 2 == 1 * 3 は成り立ちます。

10. {'A': 1, 'B': 1, 'C': 2, 'D': 1}:

    • この組み合わせも制約を満たします。1 + 1 == 2 * 1 は成り立ちます。

11. {'A': 1, 'B': 1, 'C': 1, 'D': 2}:

    • 最後の組み合わせでも制約が満たされます。1 + 1 == 1 * 2 は成り立ちます。

各解は、変数A、B、C、およびDに対する異なる値の割り当てを示し、制約 A + B == C * D を満たすことができることを示しています。

このように、CSPの解は制約を満たす変数の組み合わせを表します。