フォーカスを持っているウィンドウの領域は次のメソッドで取得できます。

1

r = App.focusedWindow()

指定したアプリが複数ウィンドウある場合、Appオブジェクトを取得しそのオブジェクトのwindow(n)メソッドを使います。
引数のnを省略するか0を指定すると最初のウィンドウを選択できます。

1
2

myApp = App("chrome")
r = myApp.window(0)

Sikuliでは、一定時間が経過すると自動的に消えるダイアログボックスを作ることができます。

1

res = Do.popup(u"10秒経過すると自動的に閉じるダイアログ", 10)    # 第２引数が待ち時間（秒）です。

時間が経過しても操作しなかったときは、戻り値はNoneとなります。

ダイアログの種類は下記の表をご参照ください。

ユーザの入力待ちで処理を止めたくない場合などに使用できるかと思います。

Sikuliでは、下記のダイアログボックスを表示することができます。

※[取消]ボタンをおした場合にはNoneが返されます。

プログラム側で領域を指定するのではなく、ユーザに範囲を選択してもらって領域を選択したいときがあります。例えば、OCR処理でテキスト化したい画面の範囲をユーザに選択させたいような場合です。

このようなときには、selectRegionメソッドを使います。

1

r = selectRegion("ユーザに表示する文字列")

selectRegionメソッドを使うと、SikuliX IDEで「Region」ボタンをクリックしたときのように画面全体がグレーアウトし、ユーザが範囲を選択できる状態になります。

ユーザが領域を選択したときは、その領域がRegionオブジェクトして返されます。
[ESC]キーを押してキャンセルしたときはNoneが返ります。

RPAは人間の目や手の動きを覚えて実行するものですが、どうやってRPAに手順を教えればいいでしょうか。大きく分けて教え方は次の３種類があります。

(1)やって見せるレコーディング機能

RPAを動かしておいて人間がパソコン上で教えたい手順を実行し、その手順をRPAに記録させ再生します。
プログラミングが不要なので最も手軽な方法です。しかし操作手順はいつも同じとは限らず、操作をかえることがよくあります。
記録した手順に判断をする処理を追加するなどしないと、実用に耐える操作手順が完成しないケースが多くあるのが実情です。

(2)フローチャート等で図示する方法

あらかじめ手順の全体像を、判断や分岐を含めて図示するのでレコーディング機能を使うよりは手間がかかります。しかしきちんと手順を教えることができます。
スクリプトの文法を覚える必要がないので比較的簡単ですが、大規模なフローチャートになると画面いっぱいに広がり入りきらなくことがよくあり、印刷する場合や手順を確認する場合に不便な面もあります。

(3)スクリプト等で示す方法

スクリプトで１行ずつ手順を書いていく方法です。
スクリプトの文法を覚える必要があり、書く量が多くなる傾向にあり難易度は高めです。
細かく手順を設定することができるので、プログラミング経験者であればこれが一番おすすめです。

Sikuliでは、画像を指定してその画像と合致する箇所を見つけますがあまりに厳格だと、少しの違いで画像が見つからなくなります。
逆に寛容だと、似ているけれど違う部分がマッチしてしまう可能性があります。

そこでSikuliではどの程度のあいまいさまでを許すかを、類似度として設定できます。
類似度は、パターン設定ウィンドウの[マッチングプレビュー]から設定することができます。
0から1の範囲の設定値で、0に近づくほどあいまいさが増し、1に近づくほど厳格になります。デフォルトは0.7です。

Sikuliでは、場所を特定するオブジェクトが５種類あります。
頭文字をとって「PSRML」と表示されます。

• Patternオブジェクト
  画像ファイル名に加え、類似度やターゲットオフセットを設定できるオブジェクトです。
  findメソッドをコールすると、見つかった場所がMatchオブジェクトとして取得できます。
• Stringオブジェクト
  画像ファイル名を指定する文字列のことです。
  類似度は0.7、ターゲットオフセットは画像の中心固定です。
  findメソッドをコールすると、見つかった場所がMatchオブジェクトとして得られます。
• Regionオブジェクト
  左上のX座標、Y座標、幅、高さで指定されたオブジェクトです。
  画像マッチではなく、座標で指定するときに使用します。
• Matchオブジェクト
  画像や文字列を指定し、それが見つかった場所を示すオブジェクトです。
• Locationオブジェクト
  位置を指定するオブジェクトです。
  幅と高さはなく、座標だけの指定です。
  クリックする場所や入力する場所など、対象位置だけを指定するときに使用します。

clickメソッドやtypeメソッドなど、クリックやキー入力する機能の引数には、上記5種類のPSRMLオブジェクトのいずれでも指定できます。
しかし最終的に、クリックしたりキー入力するときは「座標」として扱われます。
この座標は、Locationオブジェクトとして管理されるのでLocationオブジェクト以外のオブジェクトが指定された場合は、Locationオブジェクトに変換されます。

次の処理では、①で存在するかどうかをチェックし②でその場所をクリックするという２つの処理で同じ画像のマッチングをしています。

1
2
3
4

if exists("a.png"):  # ①
    click("a.png")   # ②
else:
    click("b.png")

画像マッチングは時間がかかる複雑な処理のため、Sikuliでは同じ画像マッチングを避けるための工夫があります。それはgetLastMatchメソッドです。

getLastMatchメソッドは最後に画像マッチングしたときの結果を返します。
このメソッドを使うと先ほどの処理は以下のように記述することができます。

1
2
3
4

if exists("a.png"):
    click(getLastMatch())  # 最後に画像マッチしたときの結果をクリックする
else:
    click("b.png")

変更後のソースでは同じ画像が２つ登場することがないのでプログラムが見やすくなり、さらに処理速度も向上します。

Sikuliで長い処理をしてる途中で、画像が見つからずエラーになってしまい処理が途中で止まってしまうときがあります。
こんな時処理を見直して再度最初から実行・・・としていたのですが、それを回避する素晴らしい関数があることに気づきました。

それは「setFindFailedResponse(PROMPT)」です。

例えば次のようなコードを書いて実行します。

1
2

setFindFailedResponse(PROMPT)
find("1577880270644.png")

もし指定した画像が見つからなかった場合は、エラーになるのではなく下記の確認ダイアログが表示されます。

• Retry
  見つからなかった画像が表示されるように操作しておいてから、このボタンを押すと処理を再開することができます。
• Capture/Skip
  指定していた画像を別の画像に置き換えたり（再度スクリーンショットをとる）、処理自体をスキップすることができます。
• Abort
  処理を中断することができます。

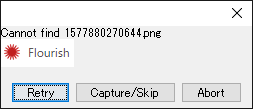
この関数を見つけてから処理を途中から再実行することができるようになり、効率があがりました。

Sikuliでは「ある画像が表示されたら処理を行う」といったイベント処理を行うことができます。

1
2
3
4
5
6
7
8

def hnd1(event):
    popup('hnd1')

r = Region(163,107,323,217)
r.onAppear("1577792749137.png", hnd1)
r.observeInBackground()

wait(10)

まずイベントがあった場合に呼ばれる関数を定義します。(hnd1関数)

あとは監視する範囲をRegionで指定し、その範囲にイベントハンドラーを設定します。(onAppear)

次にobserveInBackground()でバックグラウンドで監視処理を開始させます。
observe関数でも監視処理を始めることができますが、この場合処理が止まってしまいほかの処理が実行できなくなります。