1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
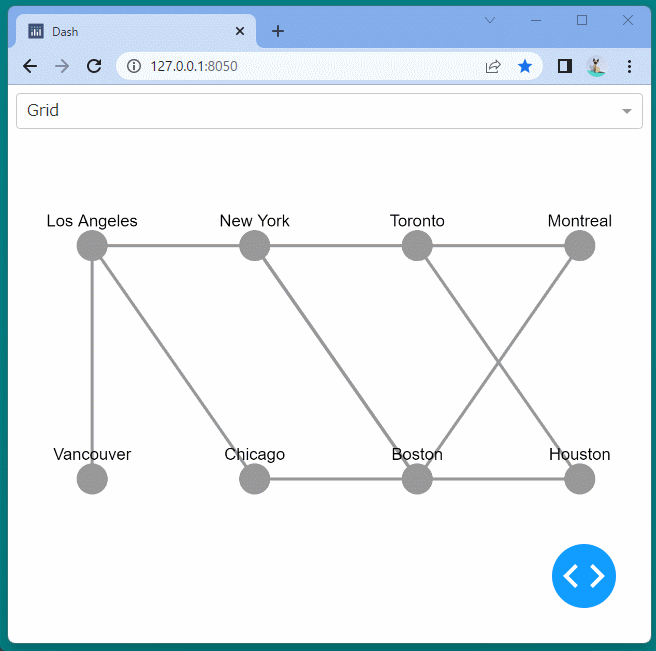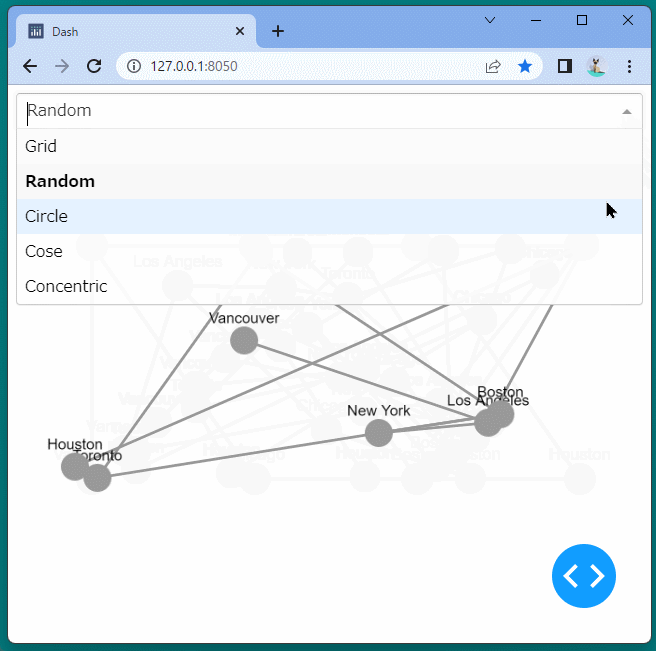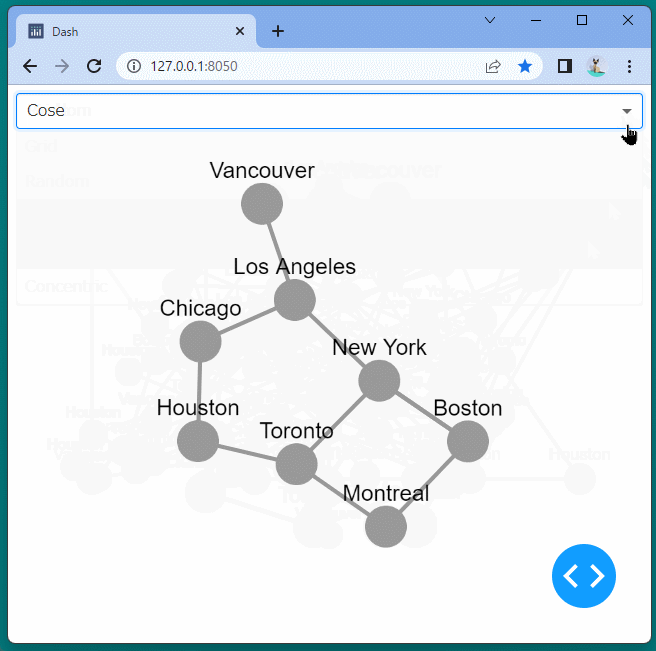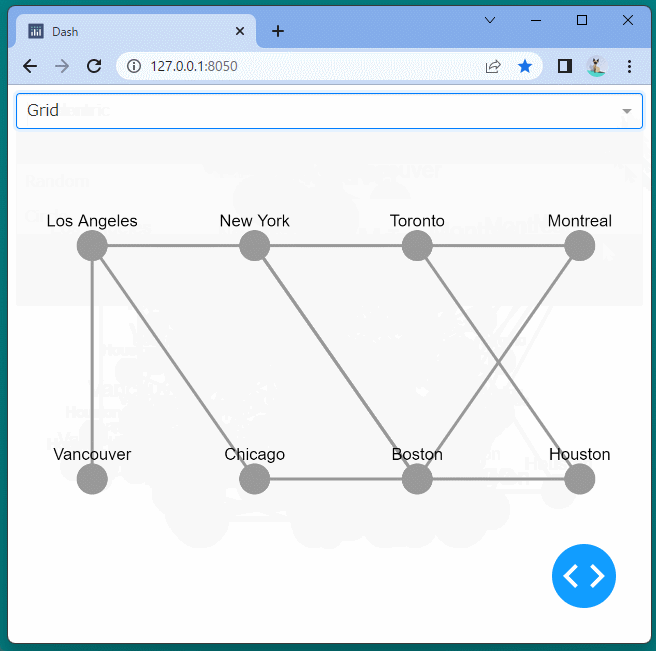
| import dash
import dash_cytoscape as cyto
import dash_html_components as html
import dash_core_components as dcc
from pprint import pprint
from dash.dependencies import Input, Output, State
app = dash.Dash(__name__)
nodes = [
{
'data': {'id': short, 'label': label},
'position': {'x': 20*lat, 'y': -20*long}
}
for short, label, long, lat in (
('la', 'Los Angeles', 34.03, -118.25),
('nyc', 'New York', 40.71, -74),
('to', 'Toronto', 43.65, -79.38),
('mtl', 'Montreal', 45.50, -73.57),
('van', 'Vancouver', 49.28, -123.12),
('chi', 'Chicago', 41.88, -87.63),
('bos', 'Boston', 42.36, -71.06),
('hou', 'Houston', 29.76, -95.37)
)
]
edges = [
{'data': {'source': source, 'target': target}}
for source, target in (
('van', 'la'),
('la', 'chi'),
('hou', 'chi'),
('to', 'mtl'),
('mtl', 'bos'),
('nyc', 'bos'),
('to', 'hou'),
('to', 'nyc'),
('la', 'nyc'),
('nyc', 'bos')
)
]
default_stylesheet = [
{
'selector': 'node',
'style': {
'background-color': '#BFD7B5',
'label': 'data(label)'
}
},
{
'selector': 'edge',
'style': {
'line-color': '#A3C4BC'
}
}
]
app.layout = html.Div([
html.Div([
html.Button('Add Node', id='btn-add-node', n_clicks_timestamp=0),
html.Button('Remove Node', id='btn-remove-node', n_clicks_timestamp=0)
]),
cyto.Cytoscape(
id='cytoscape-elements-callbacks',
layout={'name': 'cose'},
stylesheet=default_stylesheet,
style={'width': '100%', 'height': '450px'},
elements=edges+nodes
)
])
@app.callback(Output('cytoscape-elements-callbacks', 'elements'),
Input('btn-add-node', 'n_clicks_timestamp'),
Input('btn-remove-node', 'n_clicks_timestamp'),
State('cytoscape-elements-callbacks', 'elements'))
def update_elements(btn_add, btn_remove, elements):
current_nodes, deleted_nodes = get_current_and_deleted_nodes(elements)
if int(btn_add) > int(btn_remove) and len(deleted_nodes):
current_nodes.append(deleted_nodes.pop())
cy_edges = get_current_valid_edges(current_nodes, edges)
return cy_edges + current_nodes
elif int(btn_remove) > int(btn_add) and len(current_nodes):
current_nodes.pop()
cy_edges = get_current_valid_edges(current_nodes, edges)
return cy_edges + current_nodes
return elements
def get_current_valid_edges(current_nodes, all_edges):
"""Returns edges that are present in Cytoscape:
its source and target nodes are still present in the graph.
"""
valid_edges = []
node_ids = {n['data']['id'] for n in current_nodes}
for e in all_edges:
if e['data']['source'] in node_ids and e['data']['target'] in node_ids:
valid_edges.append(e)
return valid_edges
def get_current_and_deleted_nodes(elements):
"""Returns nodes that are present in Cytoscape and the deleted nodes
"""
current_nodes = []
deleted_nodes = []
for ele in elements:
if 'source' not in ele['data']:
current_nodes.append(ele)
node_ids = {n['data']['id'] for n in current_nodes}
for n in nodes:
if n['data']['id'] not in node_ids:
deleted_nodes.append(n)
return current_nodes, deleted_nodes
if __name__ == '__main__':
app.run_server(debug=True)
|