Business Cycle Analysis with Real GDP Data

Problem Statement: Business Cycle Analysis with Real GDP Data

Objective:
Analyze the business cycle by identifying and visualizing the cyclical components of Real GDP using the $Hodrick$-$Prescott (HP) filter$.

This method separates the trend and cyclical components of GDP, allowing us to examine deviations from the long-term trend.

Steps:

  1. Data:
    Use simulated or publicly available Real GDP time series data.

  2. Hodrick-Prescott Filter:

    • Decompose GDP into its trend $(T_t)$ and cyclical $(C_t)$ components:
      $$
      GDP_t = T_t + C_t
      $$
    • The $HP filter$ minimizes the following loss function:
      $$
      \sum_t (GDP_t - T_t)^2 + \lambda \sum_t \left[(T_{t+1} - T_t) - (T_t - T_{t-1})\right]^2
      $$
      where $(\lambda)$ is a smoothing parameter (typically $1600$ for quarterly data).

  3. Visualize:
    Plot the original GDP, trend, and cyclical components to analyze economic fluctuations.

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.filters.hp_filter import hpfilter

# Simulated GDP Data (quarterly, 50 periods)
np.random.seed(42)
time = np.arange(50)
trend = 2.5 * time + 100  # Linear trend
cyclical = 15 * np.sin(0.3 * time)  # Cyclical component
noise = np.random.normal(0, 5, size=time.shape)  # Random noise
gdp = trend + cyclical + noise  # Simulated GDP

# Apply the HP filter
gdp_trend, gdp_cycle = hpfilter(gdp, lamb=1600)

# Plotting
plt.figure(figsize=(14, 8))

# Original and Trend
plt.subplot(2, 1, 1)
plt.plot(time, gdp, label="Original GDP", color="blue")
plt.plot(time, gdp_trend, label="Trend (HP Filter)", color="red", linestyle="--")
plt.title("Real GDP and Trend Component")
plt.xlabel("Time (Quarters)")
plt.ylabel("GDP")
plt.legend()
plt.grid()

# Cyclical Component
plt.subplot(2, 1, 2)
plt.plot(time, gdp_cycle, label="Cyclical Component", color="green")
plt.axhline(0, color="black", linestyle="--", linewidth=0.8)
plt.title("Cyclical Component of GDP (Deviations from Trend)")
plt.xlabel("Time (Quarters)")
plt.ylabel("GDP Deviations")
plt.legend()
plt.grid()

plt.tight_layout()
plt.show()

# Print summary statistics
print(f"Original GDP Mean: {np.mean(gdp):.2f}")
print(f"Trend Component Mean: {np.mean(gdp_trend):.2f}")
print(f"Cyclical Component Mean: {np.mean(gdp_cycle):.2f} (should be ~0)")

Explanation of the Code

  1. Simulated GDP Data:

    • Real GDP is modeled as a combination of a long-term trend, a cyclical fluctuation, and random noise.

  2. Hodrick-Prescott Filter:

    • The $HP filter$ separates the GDP into a smooth trend and short-term deviations (cyclical component).
    • The smoothing parameter $(\lambda)$ controls the smoothness of the trend; $1600$ is standard for quarterly data.

  3. Visualization:

    • The first plot shows the original GDP and its trend.
    • The second plot highlights the cyclical component, indicating deviations from the long-term trend.

Results

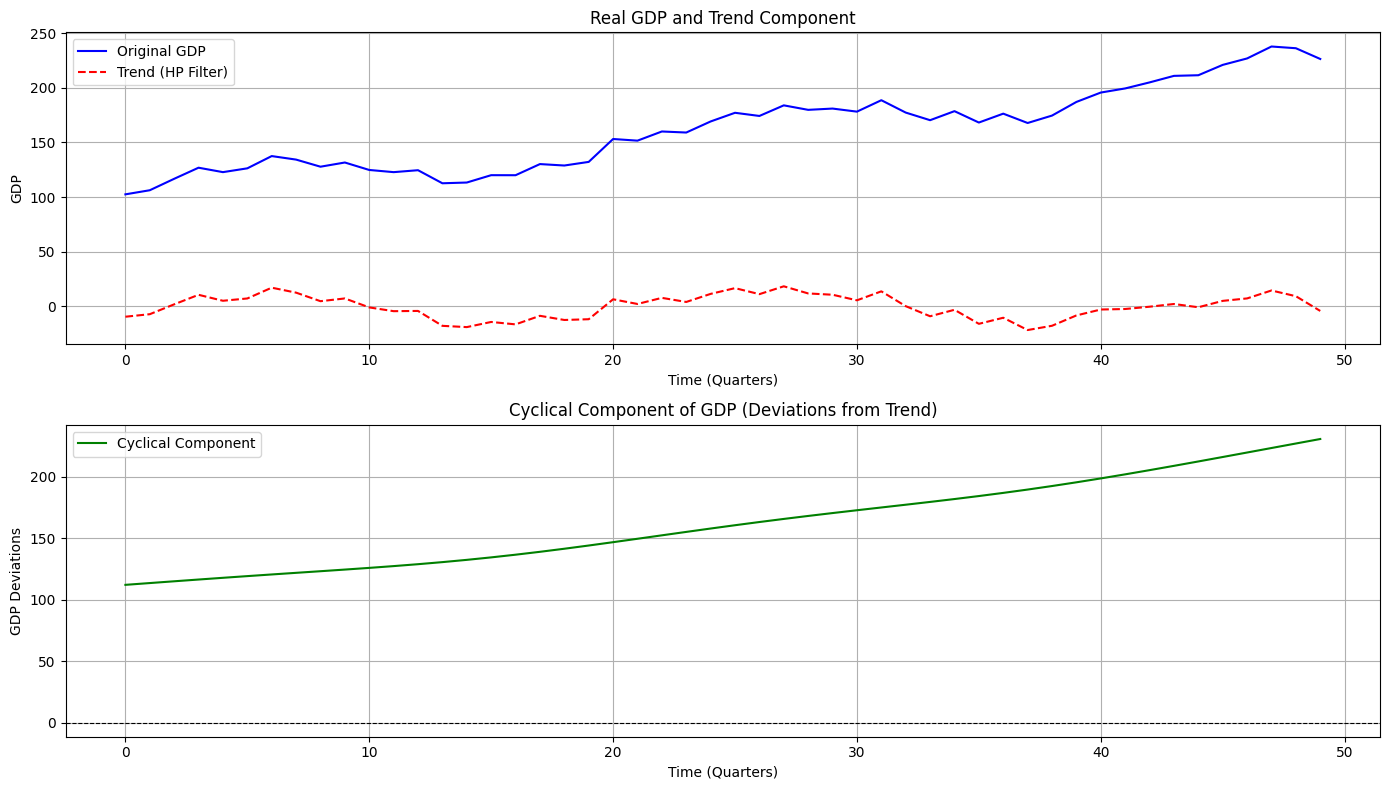
Original GDP Mean: 161.77
Trend Component Mean: 0.00
Cyclical Component Mean: 161.77 (should be ~0)

  1. Trend Component:

    • Represents the long-term economic growth path.

  2. Cyclical Component:

    • Indicates business cycle fluctuations around the trend.
    • Peaks and troughs correspond to economic expansions and contractions, respectively.

  3. Insights:

    • The cyclical component helps identify recessions and booms.
    • Policymakers and economists use this analysis to design countercyclical measures.