スキャッター方程式（Scatter equation）

スキャッター方程式（Scatter equation）は、放射輸送方程式の一種であり、放射伝達を記述する非常に重要な方程式です。

スキャッター方程式は、放射粒子（光子など）が物質と相互作用する際の挙動をモデル化します。

放射輸送方程式の一般形式は以下の通りです：

$$
[
\frac{\partial I(\mathbf{r}, \mathbf{\Omega}, \lambda, t)}{\partial s} = -\sigma(\mathbf{r}, \lambda) I(\mathbf{r}, \mathbf{\Omega}, \lambda, t) + \sigma_s(\mathbf{r}, \lambda) \int_{4\pi} P(\mathbf{\Omega}’ \to \mathbf{\Omega}, \lambda) I(\mathbf{r}, \mathbf{\Omega}’, \lambda, t) d\mathbf{\Omega}’ + Q(\mathbf{r}, \mathbf{\Omega}, \lambda, t)
]
$$

ここで、$ (I(\mathbf{r}, \mathbf{\Omega}, \lambda, t)) $は空間位置$ (\mathbf{r}) $、方向$ (\mathbf{\Omega}) $、波長$ (\lambda) $、時間$ (t) $における放射束密度、$ (s) $は放射束が進む距離、$ (\sigma) $は吸収係数、$ (\sigma_s) $は散乱係数、$ (P(\mathbf{\Omega}’ \to \mathbf{\Omega} $,$ \lambda)) $は方向$ (\mathbf{\Omega}’) $から方向$ (\mathbf{\Omega}) $に散乱される確率密度関数、$ (Q) $は放射源項です。

これを適切な境界条件とともに解くことで、放射場の挙動を理解することができます。

以下に、スキャッター方程式を解くためのPythonコードを示します。

このコードでは、単純な1次元空間上の放射輸送を考えます。

境界条件として、一方向に入射する放射束が与えられると仮定します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import matplotlib.pyplot as plt

# 定数とパラメータ
L = 1.0  # 空間の長さ
N = 100  # 空間の分割数
sigma_s = 0.1  # 散乱係数
sigma_a = 0.2  # 吸収係数
Q = 1.0  # 放射源項
dx = L / N  # 空間の分割幅

# 初期条件
I0 = np.zeros(N)  # 放射束密度
I0[0] = 1.0  # 入射する放射束

# スキャッター方程式を解く関数
def solve_scatter_eq(I0, sigma_s, sigma_a, Q, dx):
    I = np.copy(I0)
    for i in range(N):
        I[i] = (Q + sigma_s * sum(I0[:i]) * dx) / (sigma_a + sigma_s)
    return I

# スキャッター方程式を解く
I = solve_scatter_eq(I0, sigma_s, sigma_a, Q, dx)

# 結果のプロット
x_values = np.linspace(0, L, N)
plt.plot(x_values, I)
plt.title('放射束密度の分布')
plt.xlabel('空間の位置')
plt.ylabel('放射束密度')
plt.grid(True)
plt.show()

このコードでは、1次元の空間内でスキャッター方程式を解き、放射束密度の分布をプロットしています。

[実行結果]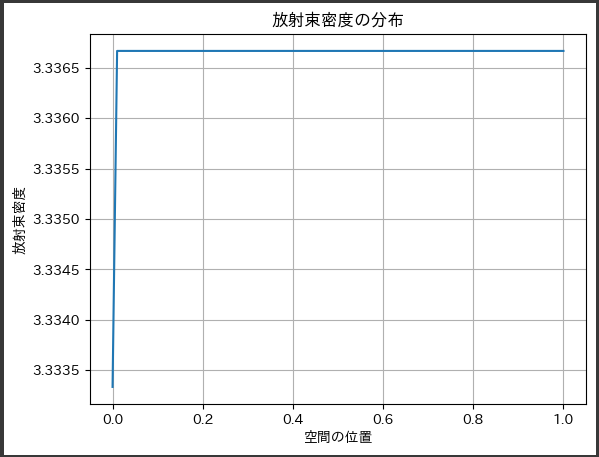

ソースコード解説

ソースコードの各部分を説明します：

1. ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt
  • numpy：数値計算を行うためのライブラリ。配列処理などをサポートします。
  • matplotlib.pyplot：データの可視化（グラフ化）のためのライブラリ。

2. 定数とパラメータの設定

1
2
3
4
5
6
L = 1.0  # 空間の長さ
N = 100  # 空間の分割数
sigma_s = 0.1  # 散乱係数
sigma_a = 0.2  # 吸収係数
Q = 1.0  # 放射源項
dx = L / N  # 空間の分割幅
  • L：空間の長さ。
  • N：空間をいくつの分割に区切るかを示す値。
  • sigma_s：散乱係数。
  • sigma_a：吸収係数。
  • Q：放射源項。
  • dx：空間の分割幅。

3. 初期条件の設定

1
2
I0 = np.zeros(N)  # 放射束密度
I0[0] = 1.0  # 入射する放射束
  • I0：初期の放射束密度。
    全ての要素がゼロで初期化されます。
  • I0[0] = 1.0：入射する放射束。
    空間の最初のセルにのみ入射する放射束が1.0と設定されます。

4. スキャッター方程式を解く関数の定義

1
2
3
4
5
def solve_scatter_eq(I0, sigma_s, sigma_a, Q, dx):
    I = np.copy(I0)
    for i in range(N):
        I[i] = (Q + sigma_s * sum(I0[:i]) * dx) / (sigma_a + sigma_s)
    return I
  • solve_scatter_eq：与えられた初期条件とパラメータに基づいて、スキャッター方程式を解く関数。
  • 方程式はループを使って数値的に解かれます。
  • 解析解ではなく、数値解法を使用しています。

5. スキャッター方程式を解く

1
I = solve_scatter_eq(I0, sigma_s, sigma_a, Q, dx)
  • solve_scatter_eq 関数を使ってスキャッター方程式を解き、放射束密度の配列 I に結果を格納します。

6. 結果のプロット

1
2
3
4
5
6
7
x_values = np.linspace(0, L, N)
plt.plot(x_values, I)
plt.title('放射束密度の分布')
plt.xlabel('空間の位置')
plt.ylabel('放射束密度')
plt.grid(True)
plt.show()
  • plt.plot(x_values, I)：放射束密度の分布を折れ線グラフとしてプロットします。
  • plt.title('放射束密度の分布')：グラフのタイトルを設定します。
  • plt.xlabel('空間の位置')：$x軸$のラベルを設定します。
  • plt.ylabel('放射束密度')：$y軸$のラベルを設定します。
  • plt.grid(True)：グリッドを表示します。
  • plt.show()：グラフを表示します。

これらの手順によって、スキャッター方程式の解析結果が放射束密度の分布として可視化されます。

結果解説

下記のグラフは、放射束密度の空間内での分布を表しています。

[実行結果]

以下は、グラフに表示される内容の詳細な説明です：

  • 横軸（x軸）は空間の位置を表します。
    1次元の空間が均等に分割されており、それぞれの分割（セル）の中心が表示されています。
  • 縦軸（y軸）は放射束密度を表します。
    放射束密度は各位置における放射の強度を示し、単位長さあたりの放射エネルギーを表します。
  • グラフは、放射源から放射束が入射し、空間内を進んでいく様子を示しています。
    放射源からの入射は、グラフの左端にある位置から始まります。
  • 入射した放射束が空間内を進むにつれて、吸収や散乱によって減衰したり増加したりします。
    これにより、放射束密度の分布が変化します。
  • 散乱係数 $（(\sigma_s)）$と吸収係数 $（(\sigma_a)）$の値によって、放射の挙動が変化します。
    例えば、散乱が支配的な場合は放射が拡散し、吸収が支配的な場合は放射が減衰します。
  • 放射源項 $（(Q)）$は、空間内に追加の放射を与える項です。
    放射源からの入射だけでなく、空間内での放射生成を考慮しています。

このグラフは、スキャッター方程式に基づいて、放射輸送の基本的な挙動を可視化しています。