有名な数学的方程式の1つとして、シュレーディンガー方程式があります。
これは量子力学における基本的な方程式であり、粒子の波動関数の時間変化を記述します。
一次元の自由粒子のシュレーディンガー方程式は以下のように表されます:
$$
i\hbar \frac{\partial}{\partial t} \Psi(x, t) = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \Psi(x, t)
$$
ここで、$ ( \Psi(x, t) ) $は波動関数、$ ( x ) $は空間座標、$ ( t ) $は時間、$ ( \hbar ) $はディラック定数、$ ( m ) $は粒子の質量です。
この方程式を解いて、時間と空間に依存する波動関数をプロットします。
1 | import numpy as np |
このコードは、一次元の自由粒子のシュレーディンガー方程式を解き、時間と空間に依存する波動関数の確率密度をプロットします。
確率密度は波動関数の絶対値の二乗として与えられ、波動関数が存在する確率を表します。
[実行結果]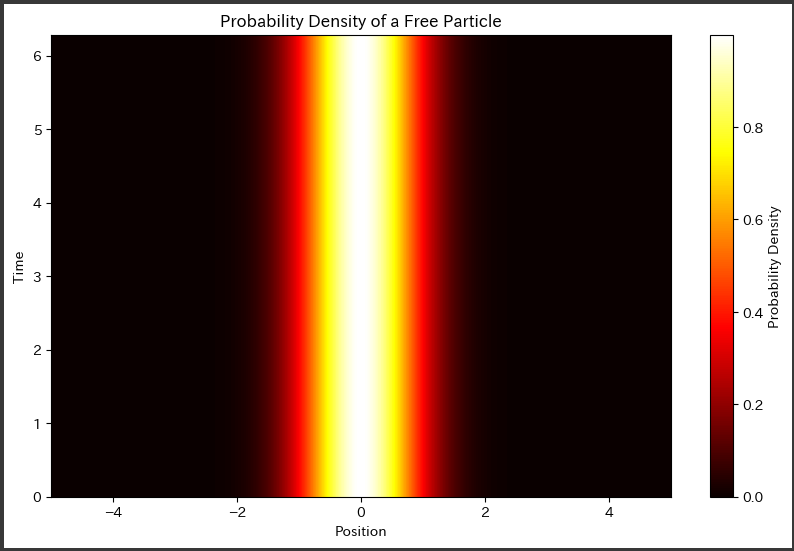
ソースコード解説
以下にソースコードを詳しく説明します。
1. import numpy as np:
- NumPy ライブラリを
npとしてインポートします。
NumPy は、数値計算を行うための強力なライブラリであり、配列操作や数学関数の計算に便利です。
2. import matplotlib.pyplot as plt:
- Matplotlib ライブラリの
pyplotモジュールをpltとしてインポートします。
Matplotlib は、グラフを描画するためのライブラリであり、pyplotモジュールはその中でも一般的に使用されます。
3. h_bar = 1.0 および m = 1.0:
- シュレーディンガー方程式に登場する定数$ ( \hbar )$(ディラック定数)と粒子の質量$ ( m ) $の値を設定します。
ここでは両方とも値を$ 1.0 $に設定しています。
4. x = np.linspace(-5, 5, 400) および t = np.linspace(0, 2*np.pi, 400):
- 空間座標$ ( x ) $および時間$ ( t ) $の範囲をそれぞれ
-5から5までの区間と0から2πまでの区間に分割し、それぞれ$ 400 $個の等間隔な点で表現します。
これにより、グラフ上で表示される座標の範囲が決まります。
5. X, T = np.meshgrid(x, t):
- NumPy の
meshgrid()関数を使って、空間座標xと時間tを格子状の座標系に変換します。
これにより、各点での波動関数の値を計算するための格子が作成されます。
6. Psi = np.exp(-(X**2)/2) * np.exp(1j * T):
- シュレーディンガー方程式の解である波動関数$ ( \Psi(x, t) ) $を計算します。
ここで、np.exp()は指数関数を計算し、1jは虚数単位を表します。
この波動関数は、時間と空間に依存する複素数で表現されます。
7. plt.figure(figsize=(10, 6)):
- Matplotlib で図を作成します。
図のサイズを幅$10$インチ、高さ$6$インチに設定しています。
8. plt.imshow(np.abs(Psi)**2, extent=(-5, 5, 0, 2*np.pi), aspect='auto', cmap='hot'):
imshow()関数を使って、波動関数の絶対値の二乗である確率密度をイメージとして表示します。extent引数は$ x $軸と$ y $軸の範囲を指定し、aspect引数はアスペクト比を自動調整するように指定します。cmap引数はカラーマップを指定します。
9. plt.colorbar(label='Probability Density'):
- カラーバーをグラフに追加し、確率密度の色に対応する値を表示します。
10. plt.title('Probability Density of a Free Particle'):
- グラフのタイトルを設定します。
11. plt.xlabel('Position') および plt.ylabel('Time'):
- $ x $軸と$ y $軸のラベルを設定します。
12. plt.show():
- グラフを表示します。
結果解説
下記のグラフは、一次元自由粒子のシュレーディンガー方程式の解に基づいて、時間と空間に依存する波動関数の確率密度を表しています。
[実行結果]
横軸は空間座標$ ( x ) $を表し、縦軸は時間$ ( t ) $を表しています。
グラフの各点における色の濃さは、その空間座標と時間における波動関数の確率密度を示しています。
色が濃い領域ほど確率密度が高く、粒子が存在する可能性が高いことを意味します。
このグラフは、波動関数の時間変化を視覚的に理解するのに役立ちます。
時間が経過するにつれて、波動関数の形状が変化し、特定の空間座標で粒子の存在確率が変動します。
特に、波動関数の振動が時間によってどのように進行し、確率密度がどのように変化するかが示されています。