宇宙の膨張 フリードマン方程式

宇宙の膨張 フリードマン方程式

宇宙の膨張を表すフリードマン方程式を考えます。

フリードマン方程式は、宇宙のスケールファクター $ ( a(t) ) $とエネルギー密度 $ ( \rho(t) ) $に関連します。

方程式は以下の通りです：

$$
H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8\pi G}{3}\rho - \frac{k}{a^2}
$$

ここで、$ ( H ) $はハッブル定数、$ ( G ) $は重力定数、$ ( k ) $は空間の曲率を表します。

また、ドットは時間に関する微分を表しています。

この方程式を解くには、初期条件やエネルギー密度などが必要です。

一般的には、標準的な宇宙論の初期条件を使用します。

以下は、Pythonを使用してこの方程式を解き、グラフ化する簡単な例です。

この例では、ハッブル定数 $ ( H_0 ) $を$1$、重力定数 $ ( G ) $を$1$、曲率 $ ( k ) $を$0$と仮定します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# フリードマン方程式
def friedmann_equation(y, t):
    H0 = 1.0  # ハッブル定数
    G = 1.0   # 重力定数
    k = 0.0   # 曲率
    rho = y[0]  # エネルギー密度

    # フリードマン方程式
    dydt = [y[1], (8 * np.pi * G / 3) * rho - k / y[0]**2]
    return dydt

# 初期条件
initial_condition = [1.0, 0.0]  # 初期エネルギー密度、初期速度

# 時間の範囲
t = np.linspace(0, 10, 1000)

# 方程式を解く
solution = odeint(friedmann_equation, initial_condition, t)

# 結果をプロット
plt.plot(t, solution[:, 0], label='Scale Factor (a(t))')
plt.xlabel('Time')
plt.ylabel('Scale Factor')
plt.title('Friedmann Equation Solution')
plt.legend()
plt.show()

この例では、初期エネルギー密度を$1$、初期速度を$0$としています。

得られた結果は、時間に対する宇宙のスケールファクターの変化を示しています。

これは、宇宙が膨張していく様子を表しています。

[実行結果]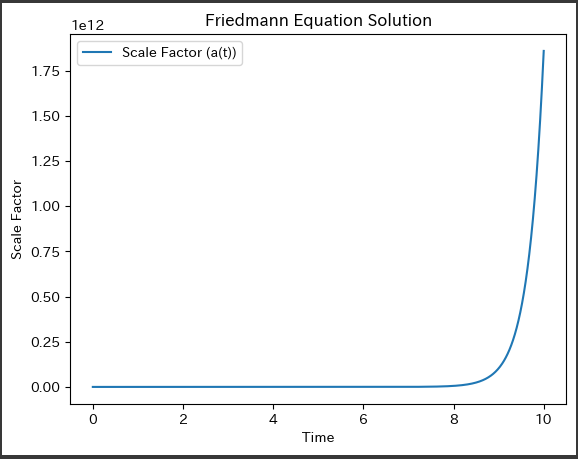

ソースコード解説

このソースコードは、Pythonを使用して宇宙の膨張を表すフリードマン方程式を解き、その解をプロットするためのものです。

以下はソースコードの章立てと詳細な説明です：

1. ライブラリのインポート

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
  • numpy：数値計算用のライブラリ。
    数学的な演算や配列操作に使用されます。
  • matplotlib.pyplot：データの可視化のためのライブラリ。
    グラフの作成や表示に利用されます。
  • scipy.integrate.odeint：常微分方程式を解くための関数が含まれています。

2. フリードマン方程式の定義

1
2
3
4
5
6
7
8
9
def friedmann_equation(y, t):
    H0 = 1.0  # ハッブル定数
    G = 1.0   # 重力定数
    k = 0.0   # 曲率
    rho = y[0]  # エネルギー密度

    # フリードマン方程式
    dydt = [y[1], (8 * np.pi * G / 3) * rho - k / y[0]**2]
    return dydt
  • friedmann_equation 関数：

フリードマン方程式を定義します。
この関数は、時間 t と状態ベクトル y を受け取り、その微分を返します。

  • H0：ハッブル定数。
    宇宙の膨張を示す定数。
  • G：重力定数。
    重力の強さを示す定数。
  • k：曲率。
    宇宙の空間が平坦か、閉じているか、開いているかを示すパラメータ。
  • rho：エネルギー密度。
    宇宙のエネルギー分布を表す。
  • dydt：微分方程式の右辺。
    宇宙の膨張を示すフリードマン方程式の微分方程式。

3. 初期条件の設定

1
initial_condition = [1.0, 0.0]  # 初期エネルギー密度、初期速度
  • initial_condition：フリードマン方程式の初期条件。
    初期エネルギー密度と初期速度が設定されています。

4. 時間の範囲の設定

1
t = np.linspace(0, 10, 1000)
  • t：時間の範囲。$0$から$10$までの範囲を等間隔に区切った$1000$のデータポイントを生成します。

5. 方程式の解の計算

1
solution = odeint(friedmann_equation, initial_condition, t)
  • odeint 関数：常微分方程式を解くための関数。
    friedmann_equation 関数、初期条件 initial_condition、時間 t を引数として渡し、方程式の解を計算します。

6. 結果のプロット

1
2
3
4
5
6
plt.plot(t, solution[:, 0], label='Scale Factor (a(t))')
plt.xlabel('Time')
plt.ylabel('Scale Factor')
plt.title('Friedmann Equation Solution')
plt.legend()
plt.show()
  • plt.plot：解をプロットします。
    横軸に時間 t、縦軸にスケールファクター a(t) をプロットします。
  • plt.xlabel：X軸のラベルを設定。
  • plt.ylabel：Y軸のラベルを設定。
  • plt.title：グラフのタイトルを設定。
  • plt.legend：凡例を表示。
  • plt.show：グラフを表示します。

このコードは、フリードマン方程式を解いて宇宙の膨張を表すグラフを生成します。

初期条件やパラメータの変更によって、グラフの形状が変わります。

結果解説

[実行結果]

上記のPythonコードで生成されるグラフは、フリードマン方程式を解いた結果、時間に対する宇宙のスケールファクター$ (a(t)) $の変化を表しています。

以下は、グラフに表示される内容の詳細な説明です：

1. 横軸（X軸） - 時間：

グラフの横軸は時間を表しています。
この例では、時間の範囲を$ (0) $から$ (10) $までとし、$ (1000) $の等間隔なデータポイントで構成されています。

2. 縦軸（Y軸） - スケールファクター $ (a(t)) $：

グラフの縦軸は宇宙のスケールファクター $ (a(t)) $を表しています。
スケールファクターは宇宙の膨張を示し、大きくなるほど宇宙が膨張していることを示します。

3. グラフの形状：

グラフは時間に対する宇宙の膨張を示しており、スケールファクターが増加していく様子を観察できます。
これは、ビッグバン理論に基づく宇宙の進化を示しています。
初期条件によってグラフの形状が変わります。

4. 初期条件：

この例では初期エネルギー密度を$ (1) $、初期速度を$ (0) $と仮定しています。
これらの初期条件に基づいて、時間が経過するにつれて宇宙がどのように膨張しているかが反映されています。

このグラフは、ビッグバンモデルにおける宇宙の膨張をシミュレートしたものであり、初期条件やパラメータの変更によって異なる結果が得られます。