常微分方程式

常微分方程式

微分方程式の例として、単純な1階の常微分方程式を取り上げましょう。

以下の例では、微分方程式 $ ( \frac{dy}{dt} = -ky ) $を考えます。

この方程式は指数減衰を表します。

これを解いて、その結果をグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# 微分方程式の定義
def model(y, t, k):
    dydt = -k * y
    return dydt

# 初期条件
y0 = 5.0

# 時間の範囲
t = np.linspace(0, 10, 100)

# パラメータ
k = 0.1

# 微分方程式を解く
solution = odeint(model, y0, t, args=(k,))

# 結果のグラフ化
plt.figure(figsize=(8, 6))
plt.plot(t, solution, label='y(t)')
plt.title('指数減衰：$\\frac{dy}{dt} = -ky$')
plt.xlabel('時間 (t)')
plt.ylabel('y(t)')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、SciPyのodeint関数を使用して微分方程式を解き、結果をグラフ化しています。

[実行結果]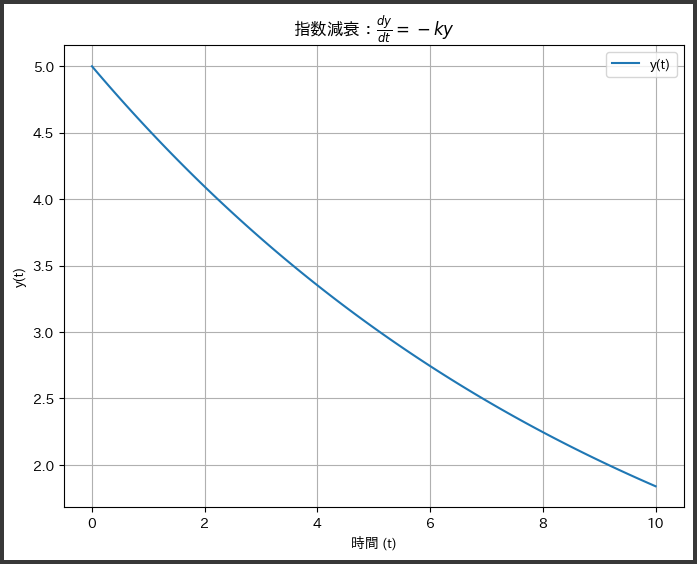

指数減衰が確認できるでしょう。

パラメータ$ (k) $を変更することで解の挙動が変わります。

ソースコード解説

以下はソースコードの詳細な説明です。

1. モジュールのインポート:

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
  • numpy: 数値計算用ライブラリで、数値配列や数学関数などを提供します。
  • matplotlib.pyplot: グラフの描画に使用されるライブラリ。
  • scipy.integrate.odeint: 常微分方程式を数値的に解くための関数が含まれているSciPyライブラリの一部。

2. 微分方程式の定義:

1
2
3
def model(y, t, k):
   dydt = -k * y
   return dydt
  • model関数は、微分方程式$ ( \frac{dy}{dt} = -ky ) $の右辺を定義しています。
    この関数は odeint 関数によって呼び出されます。

3. 初期条件の設定:

1
y0 = 5.0
  • 微分方程式の初期条件$ (y(0)) $を設定します。

4. 時間の範囲の設定:

1
t = np.linspace(0, 10, 100)
  • 時間の範囲を$0$から$10$までの区間を$100$点で均等に区切って定義します。

5. パラメータの設定:

1
k = 0.1
  • 微分方程式のパラメータ$ (k) $を設定します。

6. 微分方程式を解く:

1
solution = odeint(model, y0, t, args=(k,))
  • odeint 関数を使用して微分方程式を解きます。
    初期条件 y0、時間の範囲 t、およびパラメータ k を指定しています。

7. 結果のグラフ化:

1
2
3
4
5
6
7
8
plt.figure(figsize=(8, 6))
plt.plot(t, solution, label='y(t)')
plt.title('指数減衰：$\\frac{dy}{dt} = -ky$')
plt.xlabel('時間 (t)')
plt.ylabel('y(t)')
plt.legend()
plt.grid(True)
plt.show()
  • matplotlib を使用して、微分方程式の解 solution を時間に対してプロットし、グラフを表示します。
  • グラフのタイトル、軸ラベル、凡例、グリッドが設定されています。

このプログラムは、指数減衰を示す微分方程式を数値的に解き、その解をグラフで視覚化する基本的な例です。

結果解説

[実行結果]

以下はグラフに表示される内容の詳細な説明です。

横軸 (X軸):時間$ (t) $

$0$から$10$の範囲を$100$点で等分しています。

縦軸 (Y軸):変数$ (y(t))$

微分方程式の解であり、指数減衰の挙動を示します。
初期条件$ (y(0)) $は$ 5.0 $としています。

グラフの線:

微分方程式を解いた結果の$ (y(t)) $の変化を表しています。
指数減衰の特徴的な形状で、初めは急速に減少し、後に緩やかな減少に移ります。

グラフのタイトル:指数減衰：$ \frac{dy}{dt} = -ky $

微分方程式の性質と解いたものが指数減衰を示すことを示しています。

X軸およびY軸のラベル:

時間（時間$ (t)$）および変数$ (y(t)) $の説明があります。

凡例 (Legend):$y(t)$

グラフ内の線が何を示しているかを示すラベルです。

グリッド:

グラフ内に格子状の線が描かれ、視認性を向上させています。

このグラフは、微分方程式の解を通して、指数減衰が時間とともにどのように進行するかを示しています。

指数減衰は、物理学や生態学などのさまざまな分野で重要な概念であり、この例ではPythonを用いて簡単に表現されています。