流体力学 ナビエ・ストークス方程式

流体力学 ナビエ・ストークス方程式

流体力学に関連する方程式として、ナビエ・ストークス方程式が代表的です。

これは流体の運動を記述する偏微分方程式であり、以下のように表されます：

1. 質量保存の式（連続の式）:

$$
\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0
$$

2. 運動方程式（運動量保存の式）:

$$
\rho \left( \frac{\partial \mathbf{v}}{\partial t} + \mathbf{v} \cdot \nabla \mathbf{v} \right) = - \nabla p + \mu \nabla^2 \mathbf{v} + \mathbf{f}
$$

ここで、$ (\rho) $は流体の密度、$ (\mathbf{v}) $は流速ベクトル、$ (p) $は圧力、$ (\mu) $は動粘性係数、$ (\mathbf{f}) $は体積力ベクトルです。

この方程式をPythonで解き、結果をグラフ化するには、適切な境界条件と数値解法を選択する必要があります。

一般的には有限体積法や有限要素法などの手法が用いられますが、ここでは簡単な場合として1次元の運動のみを考え、有限差分法を用いてナビエ・ストークス方程式を解く方法を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
L = 1.0  # ドメインの長さ
Nx = 100  # 空間格子点数
Nt = 1000  # 時間ステップ数
dx = L / Nx  # 空間刻み
dt = 0.001  # 時間刻み
nu = 0.01  # 動粘性係数
rho = 1.0  # 流体の密度
force = 1.0  # 外力

# 初期条件設定
u = np.zeros(Nx)  # 流速
u[int(0.5 / dx):int(0.6 / dx)] = 1.0  # 初期条件: 一部の領域に初速度を与える

# シミュレーション
for t in range(Nt):
    un = np.copy(u)
    for i in range(1, Nx-1):
        u[i] = un[i] - dt / (2 * dx) * (un[i+1]**2 - un[i-1]**2) + \
               nu * dt / dx**2 * (un[i+1] - 2*un[i] + un[i-1]) + \
               dt / rho * force

# 結果のプロット
x = np.linspace(0, L, Nx)
plt.plot(x, u)
plt.xlabel('Position')
plt.ylabel('Velocity')
plt.title('1D Navier-Stokes Simulation')
plt.show()

このコードは、1次元の流れにおけるナビエ・ストークス方程式を解き、結果をプロットします。

初期条件として、ドメインの中央部分にのみ初速度が与えられます。

流速の時間変化をプロットすることで、流れの挙動を可視化することができます。

[実行結果]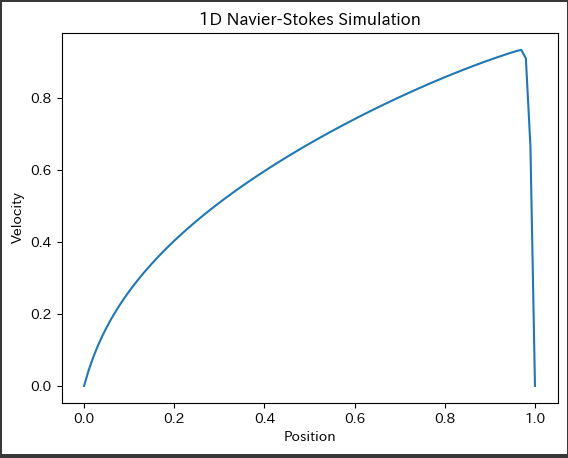

ソースコード解説

ソースコードを詳しく説明します。

ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt
  • NumPy: 数値計算を行うためのライブラリ。
  • Matplotlib: グラフの描画に使用されるライブラリ。

パラメータ設定

1
2
3
4
5
6
7
8
L = 1.0  # ドメインの長さ
Nx = 100  # 空間格子点数
Nt = 1000  # 時間ステップ数
dx = L / Nx  # 空間刻み
dt = 0.001  # 時間刻み
nu = 0.01  # 動粘性係数
rho = 1.0  # 流体の密度
force = 1.0  # 外力
  • L: シミュレーションする空間の長さ。
  • Nx: 空間を離散化する格子点の数。
  • Nt: 時間を離散化するステップ数。
  • dx: 空間刻み。
  • dt: 時間刻み。
  • nu: 流体の動粘性係数。
  • rho: 流体の密度。
  • force: 外力の強さ。

初期条件設定

1
2
u = np.zeros(Nx)  # 流速
u[int(0.5 / dx):int(0.6 / dx)] = 1.0  # 初期条件: 一部の領域に初速度を与える
  • u: 流速を表す配列。
    最初は全ての要素がゼロに初期化されています。
  • u[int(0.5 / dx):int(0.6 / dx)] = 1.0: 流速の一部の領域に初速度を与えています。
    この範囲はドメインの中心付近です。

シミュレーション

1
2
3
4
5
6
for t in range(Nt):
    un = np.copy(u)
    for i in range(1, Nx-1):
        u[i] = un[i] - dt / (2 * dx) * (un[i+1]**2 - un[i-1]**2) + \
               nu * dt / dx**2 * (un[i+1] - 2*un[i] + un[i-1]) + \
               dt / rho * force
  • ループを使用して、時間ステップごとに流体の状態を更新します。
  • 2重のループを使用して、空間内の各格子点での更新を行います。
  • ナビエ・ストークス方程式の離散化バージョンを用いて、流速を更新しています。

結果のプロット

1
2
3
4
5
6
x = np.linspace(0, L, Nx)
plt.plot(x, u)
plt.xlabel('Position')
plt.ylabel('Velocity')
plt.title('1D Navier-Stokes Simulation')
plt.show()
  • シミュレーションの結果をグラフ化します。
  • x: ドメイン内の位置の配列。
  • plt.plot(x, u): 位置に対する流速をプロットします。
  • plt.xlabel('Position'): x軸のラベルを設定します。
  • plt.ylabel('Velocity'): y軸のラベルを設定します。
  • plt.title('1D Navier-Stokes Simulation'): グラフのタイトルを設定します。
  • plt.show(): グラフを表示します。

結果解説

[実行結果]

このグラフは、1次元のナビエ・ストークス方程式を解いた結果であり、横軸には空間の位置、縦軸には流速を示しています。

具体的には、以下の内容がグラフに表示されます：

1. 位置（横軸）:

ドメインの長さに対する位置が横軸に表示されます。
ドメインの左端から右端までを表し、単位は任意の長さの単位（例えばメートル）になります。

2. 流速（縦軸）:

流体の速度が縦軸に表示されます。
流速は時間とともに変化し、位置によっても異なります。
流速の単位は長さの単位に時間の逆数を掛けたものになります（例えば m/s）。

3. グラフの形状:

初期条件として一部の領域に初速度が与えられているため、その部分の流速が一定であることが分かります。
その他の部分では、時間とともに流速が変化していることが示されています。
流体の流れがどのように振る舞うかは、初期条件や境界条件、流体の性質（動粘性係数や密度）に依存します。

4. タイトルと軸ラベル:

グラフには、図の内容を説明するためのタイトルと軸ラベルが付いています。
タイトルには「1D Navier-Stokes Simulation」とあり、1次元のナビエ・ストークス方程式のシミュレーション結果であることが示されています。

$x軸$には「Position」（位置）が、$y軸$には「Velocity」（流速）が表示されています。