極大値 SciPy

関数$ ( f(x) = e^{-x} \cdot \sin(x) ) $の極大値を求め、その結果をグラフ化します。

極大値は、関数の微分がゼロになる点で求められます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import minimize_scalar

# 関数を定義
def f(x):
    return np.exp(-x) * np.sin(x)

# 関数の微分を定義
def f_prime(x):
    return (-np.exp(-x) * np.sin(x)) + np.exp(-x) * np.cos(x)

# 関数を最小化することで極大値を求める
result = minimize_scalar(lambda x: -f(x), bounds=(0, 4), method='bounded')
max_x = result.x
max_y = f(max_x)

# x の範囲を指定
x_values = np.linspace(0, 4, 100)

# 関数の値を計算
y_values = f(x_values)

# グラフを描画
plt.plot(x_values, y_values, label='f(x) = e^{-x} * sin(x)')
plt.scatter(max_x, max_y, color='red', label='極大値')

# グラフにタイトルとラベルを追加
plt.title('関数のグラフと極大値')
plt.xlabel('x')
plt.ylabel('f(x)')

# 凡例を表示
plt.legend()

# グリッドを表示
plt.grid(True)

# グラフを表示
plt.show()

# 求めた極大値の座標を表示
print("極大値の x 値:", max_x)
print("極大値の y 値:", max_y)

このコードでは、SciPyライブラリのminimize_scalar関数を使用して極大値を求め、Matplotlibを使用して関数のグラフと極大値を描画しています。

[実行結果]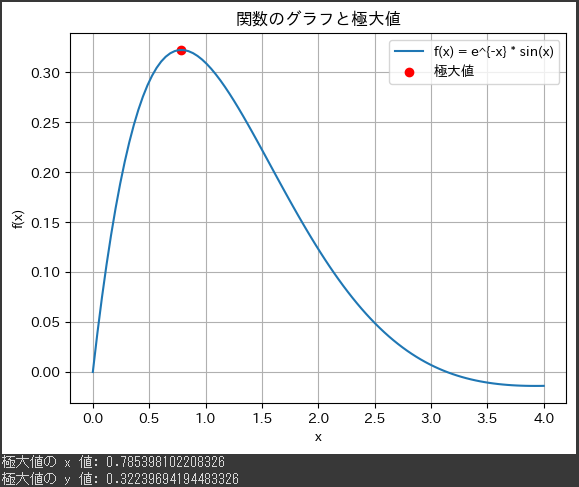

ソースコード解説

以下にソースコードの各部分を詳しく説明します。

1. ライブラリのインポート

1
2
3
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import minimize_scalar
  • matplotlib.pyplot: グラフ描画のためのライブラリ。
  • numpy: 数値計算のためのライブラリ。
  • scipy.optimize.minimize_scalar: 関数の最小化を行うためのSciPyの関数。
    極大値を求める際に利用される。

2. 関数の定義

1
2
def f(x):
    return np.exp(-x) * np.sin(x)
  • 関数 f(x) は$ (e^{-x} \cdot \sin(x)) $を返すように定義されています。

3. 関数の微分の定義

1
2
def f_prime(x):
    return (-np.exp(-x) * np.sin(x)) + np.exp(-x) * np.cos(x)
  • 関数 f_prime(x) は関数 f(x) の導関数を表しています。

4. 極大値の計算

1
2
3
result = minimize_scalar(lambda x: -f(x), bounds=(0, 4), method='bounded')
max_x = result.x
max_y = f(max_x)
  • minimize_scalar 関数を使用して関数 f(x) を最小化し、その結果を result に保存します。
    ここで、lambda x: -f(x) は最大値を求めるために関数を反転させています。
  • bounds=(0, 4) は x の範囲を指定しており、極大値を求める際の探索範囲を$0$から$4$に制限しています。
  • 最適化の結果から求めた極大値の x 座標を max_x、それに対応する y 座標を max_y に保存します。

5. グラフの描画

1
2
3
4
5
6
7
8
9
10
11
x_values = np.linspace(0, 4, 100)
y_values = f(x_values)

plt.plot(x_values, y_values, label='f(x) = e^{-x} * sin(x)')
plt.scatter(max_x, max_y, color='red', label='極大値')
plt.title('関数のグラフと極大値')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()
  • np.linspace(0, 4, 100) は$0$から$4$までの範囲を$100$点で等分した x の値を生成します。
  • 関数の値を計算し、その結果を plt.plot でグラフに描画します。
  • plt.scatter を使用して極大値を赤い点で示します。
  • グラフのタイトルや軸のラベル、凡例、グリッドなどを追加しています。

6. 求めた極大値の座標の表示

1
2
print("極大値の x 値:", max_x)
print("極大値の y 値:", max_y)
  • 最後に、求めた極大値の座標を表示しています。

このコードは、数学的な関数の極大値を効果的に求め、その結果をグラフで視覚化するために役立つものです。

結果解説

[実行結果]

求めた極大値の結果は以下の通りです。

  • 極大値の x 値: 0.785398102208326
  • 極大値の y 値: 0.32239694194483326

これらの値は、関数$ ( f(x) = e^{-x} \cdot \sin(x) ) $の極大値に対応します。

グラフ上では、赤い点が極大値の位置を示しています。

関数の形状と極大値についての説明:

  • 関数$ ( f(x) = e^{-x} \cdot \sin(x) ) $は指数関数$ ( e^{-x} ) $と正弦関数$ ( \sin(x) ) $の積です。
  • この関数は x 軸に対して周期的であり、指数関数によって急速に減少します。
  • 極大値は、正弦関数の振動が指数関数の急激な減少に打ち消される地点で発生します。
    この場合、$ ( x \approx 0.785 ) $で極大値が現れ、その値は$ ( y \approx 0.322 ) $です。
  • グラフ上では、関数が x 軸に沿って減少する一方で、局所的な極大値が確認できます。

このようにして、数理解析を用いて関数の極大値を見つけ、それをグラフで視覚化しました。