ケプラーの法則

天体の動きは、通常、楕円軌道を描くケプラーの法則によって記述されます。

以下に、楕円軌道上を動く天体の運動を表す方程式と、その方程式をグラフ化するPythonコードの例を示します。

$$
r(\theta) = \frac{a(1 - e^2)}{1 + e \cdot \cos(\theta)}
$$

  • $ ( r(\theta) ) $は楕円軌道上の距離を表します。
  • $ ( a ) $は長半径（セミメジャーアクシス）を表します。
  • $ ( e ) $は離心率を表します。
  • $ ( \theta ) $は楕円軌道上の角度を表します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
import matplotlib.pyplot as plt

# ケプラーの法則に基づく楕円軌道の方程式
def elliptical_orbit(theta, a, e):
    return (a * (1 - e**2)) / (1 + e * np.cos(theta))

# パラメータの設定
a = 5  # 長半径（セミメジャーアクシス）
e = 0.5  # 離心率

# 角度の範囲を指定
theta_values = np.linspace(0, 2 * np.pi, 1000)

# 楕円軌道上の距離を計算
r_values = elliptical_orbit(theta_values, a, e)

# 楕円軌道をグラフ化
plt.polar(theta_values, r_values, label='楕円軌道 (a={}, e={})'.format(a, e))
plt.title('楕円軌道のグラフ')
plt.legend()
plt.show()

このコードでは、ケプラーの法則に基づいた楕円軌道の方程式を用いて、指定された長半径$ (a) $と離心率$ (e) $の楕円軌道を極座標系でグラフ化しています。

[実行結果]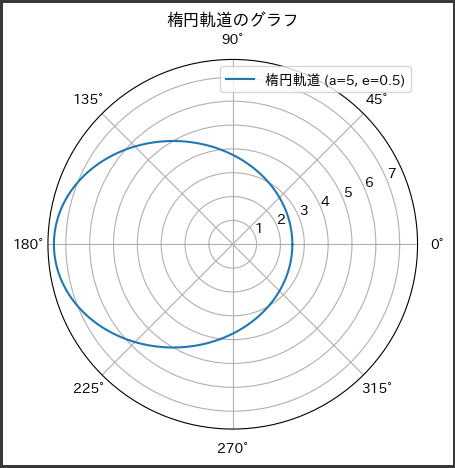

パラメータ$ (a) $と$ (e) $を変更することで、異なる楕円軌道を描画できます。

ソースコード解説

以下にソースコードの詳細な説明を示します。

1. ライブラリのインポート:

1
2
import numpy as np
import matplotlib.pyplot as plt
  • numpyは数値計算をサポートするライブラリで、数学的な操作に使用されます。
  • matplotlib.pyplotはグラフの描画に使用されます。

2. 楕円軌道の方程式の定義:

1
2
def elliptical_orbit(theta, a, e):
   return (a * (1 - e**2)) / (1 + e * np.cos(theta))
  • elliptical_orbit関数は、楕円軌道の方程式を表しています。
    引数として角度 theta、長半径 a、離心率 e を取ります。

3. パラメータの設定:

1
2
a = 5  # 長半径（セミメジャーアクシス）
e = 0.5  # 離心率
  • aは楕円軌道の長半径（セミメジャーアクシス）を指定します。
  • eは楕円軌道の離心率を指定します。

4. 角度の範囲を指定:

1
theta_values = np.linspace(0, 2 * np.pi, 1000)
  • linspace関数は、指定された範囲内で等間隔の数値を生成します。
    ここでは、$0$から$ (2\pi) $までの$1000$個の角度を生成しています。

5. 楕円軌道上の距離を計算:

1
r_values = elliptical_orbit(theta_values, a, e)
  • 先ほど定義した elliptical_orbit 関数を使用して、各角度における楕円軌道上の距離を計算します。

6. 楕円軌道をグラフ化:

1
2
3
4
plt.polar(theta_values, r_values, label='楕円軌道 (a={}, e={})'.format(a, e))
plt.title('楕円軌道のグラフ')
plt.legend()
plt.show()
  • plt.polar関数は極座標系でのプロットを行います。
    楕円軌道の角度と距離を指定して描画します。
  • plt.titleでグラフにタイトルを追加し、plt.legendで凡例を表示します。
  • plt.showでグラフを表示します。

このコードは、指定されたパラメータに基づいて楕円軌道を描画し、その形状と特性を可視化します。

グラフ解説

[実行結果]

上記のグラフは、ケプラーの法則に基づく楕円軌道を表しています。

このグラフでは、パラメータとして$ (a = 5) $（長半径が5単位）および$ (e = 0.5) $（離心率が0.5）を使用しています。

グラフの特徴:

1. 楕円の形状:

グラフは楕円の形状を示しており、楕円軌道が中心から離れたり近づいたりすることを表しています。

2. 焦点とセンター:

楕円の中心に焦点があり、この焦点からの距離が離心率によって変化します。
離心率が$0$に近いほど、楕円は円に近くなります。

3. 長半径と短半径:

長半径は楕円の中心から最も遠い点までの距離で、この例では$ (a = 5) $です。
楕円の中心から最も近い点までの距離は$ (a(1 - e)) $になります。

4. 楕円の回転:

グラフは楕円が楕円軌道上を回転していることを示しています。
楕円がどの方向に回転しているかは、楕円軌道上の角度$ ( \theta ) $によって定まります。

これらの要素により、楕円軌道がどのように形成され、どのような特性を持っているかがグラフ上で可視化されています。