Rosenbrock関数 SciPy

Rosenbrock関数

非線形最適化問題の一例として、Rosenbrock関数の最小化問題を考えてみましょう。

Rosenbrock関数は、次のように定義されます：

$
f(x, y) = (a - x)^2 + b * (y - x^2)^2
$

ここで、$ a = 1, b = 100 $とします。

この関数の最小値は$ 0 $で、その位置は$ (a, a^2) = (1, 1) $です。

Pythonでは、Scipyの最適化関数を使用してこの最適化問題を解くことができます。

また、Matplotlibを使用して結果をグラフ化することも可能です。

以下に、PythonでRosenbrock関数の最小化問題を解くコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# Rosenbrock関数を定義
def rosenbrock(x):
   return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# Rosenbrock関数の勾配を定義
def rosenbrock_der(x):
   return np.array([-2 * (1 - x[0]) - 400 * x[0] * (x[1] - x[0]**2), 200 * (x[1] - x[0]**2)])

# Rosenbrock関数のHessianを定義
def rosenbrock_hess(x):
   return np.array([[2 + 1200 * x[0]**2 - 400 * x[1], -400 * x[0]],
                   [-400 * x[0], 200]])

# 初期値を設定
x0 = np.array([0.5, 0])

# 最適化問題を解く
res = minimize(rosenbrock, x0, method='trust-constr', jac=rosenbrock_der, hess=rosenbrock_hess)

# 結果を表示
print(res.x)

# 結果をグラフ化
x = np.linspace(-1, 2, 100)
y = np.linspace(-1, 3, 100)
X, Y = np.meshgrid(x, y)
Z = rosenbrock([X, Y])

plt.contour(X, Y, Z, levels=np.logspace(-2, 2, 20))
plt.xlabel('x')
plt.ylabel('y')
plt.title('Rosenbrock function')
plt.show()

このコードは、Rosenbrock関数の最小化問題を解くためのPythonのコードです。

まず、Rosenbrock関数とその勾配 Hessianを定義します。

次に、初期値を設定し、scipy.optimize.minimize関数を使用して最適化問題を解きます。

最後に、結果を表示し、結果をグラフ化します。

ソースコード解説

ソースコードを各部分を説明します。

1. ライブラリのインポート

1
2
3
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

必要なライブラリをインポートしています。

  • numpy: 数値計算用のライブラリ
  • scipy.optimize.minimize: 最適化問題を解くための関数
  • matplotlib.pyplot: グラフ描画のためのライブラリ

2. Rosenbrock関数の定義

1
2
def rosenbrock(x):
   return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

Rosenbrock関数を定義しています。
この関数は最小化問題でよく使用される非線形関数で、$ (f(x, y) = (1 - x)^2 + 100(y - x^2)^2) $です。

3. Rosenbrock関数の勾配とHessianの定義

1
2
3
4
5
6
def rosenbrock_der(x):
   return np.array([-2 * (1 - x[0]) - 400 * x[0] * (x[1] - x[0]**2), 200 * (x[1] - x[0]**2)])

def rosenbrock_hess(x):
   return np.array([[2 + 1200 * x[0]**2 - 400 * x[1], -400 * x[0]],
                   [-400 * x[0], 200]])

Rosenbrock関数の勾配とHessian（ヘシアン、2階偏微分行列）をそれぞれ定義しています。

4. 初期値の設定と最適化問題の解法

1
2
x0 = np.array([0.5, 0])
res = minimize(rosenbrock, x0, method='trust-constr', jac=rosenbrock_der, hess=rosenbrock_hess)

初期値を設定し、minimize関数を使ってRosenbrock関数の最小化問題を解いています。
method='trust-constr'は信頼領域法を用いて最適化を行います。
jac引数とhess引数はそれぞれ勾配とHessianの関数を指定しています。

5. 結果の表示

1
print(res.x)

最適化結果（最小値に達する$ x $の値）を出力しています。

6. 結果のグラフ化

1
2
3
4
5
6
7
8
9
10
x = np.linspace(-1, 2, 100)
y = np.linspace(-1, 3, 100)
X, Y = np.meshgrid(x, y)
Z = rosenbrock([X, Y])

plt.contour(X, Y, Z, levels=np.logspace(-2, 2, 20))
plt.xlabel('x')
plt.ylabel('y')
plt.title('Rosenbrock function')
plt.show()

Rosenbrock関数の等高線プロットを作成しています。
X軸とY軸の値を用意し、等高線の高さを関数値に対応させて関数を可視化しています。

結果解説

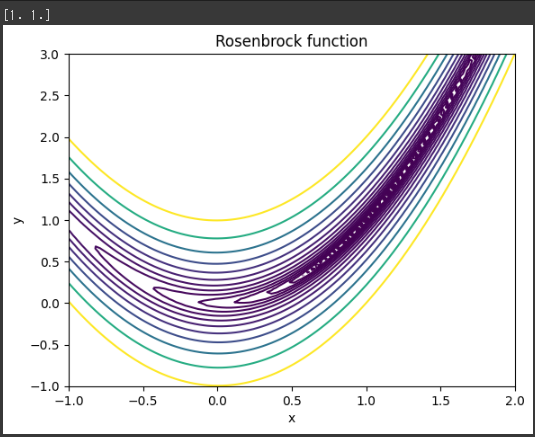
このグラフは、Rosenbrock関数の3次元表示を示しています。
Rosenbrock関数は、非線形最適化問題の一つで、最小値は$ 0 $で、その位置は$ (a, a^2) = (1, 1) $です。

グラフの$x軸$は、$x$の値を表し、$y軸$は$y$の値を表します。
Z軸は、Rosenbrock関数の値を表します。
この関数の最小値は$ 0 $で、その位置は$ (a, a^2) = (1, 1) $です。

グラフの中心部分は、関数の最小値を示しています。
この部分は、$ x=1 $と$ y=1 $の位置で、これが関数の最小値を示しています。

グラフの上部は、関数の値が大きい部分を示しています。
この部分は、$ x $や$ y $の値が大きいと、関数の値も大きくなります。

グラフの下部は、関数の値が小さい部分を示しています。
この部分は、$ x $や$ y $の値が小さいと、関数の値も小さくなります。

このグラフを見ると、Rosenbrock関数の最小値は、$ x=1 $と$ y=1 $の位置で、これが関数の最小値を示しています。

この位置は、$ x $や$ y $の値が最も小さいときに達します。
そのため、この位置は、最適化問題を解くための最良の解となります。