月と地球の運動 matplotlib

月と地球の運動

月と地球の運動をPythonを使って3Dで表現してみます。

このコードでは、地球が静止していると仮定し、月の動きのみを描画します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# 定数定義
G = 6.67430e-11  # 万有引力定数
m1 = 5.972e24  # 地球の質量(kg)
m2 = 7.35e22  # 月の質量(kg)
r = 384400000  # 地球から月までの距離(m)
v1 = 0  # 地球の初期速度(m/s)
v2 = 1022  # 月の初期速度(m/s)
timestep = 1000  # タイムステップ
num_steps = 10000  # ステップ数

# 初期条件
x1, y1, z1 = 0, 0, 0  # 地球の初期位置
x2, y2, z2 = r, 0, 0  # 月の初期位置

# 速度成分
vx1, vy1, vz1 = v1, 0, 0
vx2, vy2, vz2 = 0, v2, 0

# 位置、速度の更新
x1_values, y1_values, z1_values = [], [], []
x2_values, y2_values, z2_values = [], [], []

for _ in range(num_steps):
    # 地球と月の距離
    dx = x2 - x1
    dy = y2 - y1
    dz = z2 - z1
    r = np.sqrt(dx ** 2 + dy ** 2 + dz ** 2)

    # 万有引力の計算
    F = G * m1 * m2 / r ** 2

    # 重力の影響による加速度
    ax1 = F * dx / r / m1
    ay1 = F * dy / r / m1
    az1 = F * dz / r / m1
    ax2 = -F * dx / r / m2
    ay2 = -F * dy / r / m2
    az2 = -F * dz / r / m2

    # 速度の更新
    vx1 += ax1 * timestep
    vy1 += ay1 * timestep
    vz1 += az1 * timestep
    vx2 += ax2 * timestep
    vy2 += ay2 * timestep
    vz2 += az2 * timestep

    # 位置の更新
    x1 += vx1 * timestep
    y1 += vy1 * timestep
    z1 += vz1 * timestep
    x2 += vx2 * timestep
    y2 += vy2 * timestep
    z2 += vz2 * timestep

    # 位置を保存
    x1_values.append(x1)
    y1_values.append(y1)
    z1_values.append(z1)
    x2_values.append(x2)
    y2_values.append(y2)
    z2_values.append(z2)

# 3D軌道のプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x2_values, y2_values, z2_values, label='Moon')
ax.plot([0], [0], [0], marker='o', markersize=8, color='blue', label='Earth')
ax.set_xlabel('X coordinate (m)')
ax.set_ylabel('Y coordinate (m)')
ax.set_zlabel('Z coordinate (m)')
ax.set_title('Moon Orbit around Earth')
ax.legend()
plt.show()

このコードは、月の軌道を3Dで描画し、地球を静止して描画します。

月は地球の周りを楕円軌道で回る様子が視覚化されます。

ソースコード解説

コードの各部分を詳しく見ていきましょう：

1. ライブラリのインポート:

  • import matplotlib.pyplot as plt: プロット用のMatplotlibライブラリをインポートします。
  • from mpl_toolkits.mplot3d import Axes3D: 3Dグラフを作成するためのAxes3Dをインポートします。
  • import numpy as np: 数値計算のためのNumPyライブラリをインポートします。

2. 定数の定義:

  • G = 6.67430e-11など、物理定数（万有引力定数など）や天体の質量、初期位置、速度などの値を定義します。

3. 初期条件:

  • x1, y1, z1など、地球と月の初期位置を設定します。

4. 速度成分:

  • vx1, vy1, vz1など、地球と月の初期速度を設定します。

5. 位置、速度の更新:

  • forループ内で、地球と月の位置および速度を時間ステップごとに計算して更新します。ニュートンの運動方程式と万有引力の法則に基づいて、加速度を計算し、それをもとに速度と位置を更新します。

6. 位置の保存:

  • 各ステップでの地球と月の位置を保存するためのリストを作成し、更新された位置をそれぞれのリストに追加します。

7. 3D軌道のプロット:

  • 地球と月の位置を元に、3Dグラフを作成します。
  • figとaxを使用して3Dグラフを作成し、plotメソッドで月の軌道を、plotメソッドとmarkerを使用して地球を示します。
  • 軸ラベル、タイトル、凡例を設定しています。

最後に、plt.show()で作成したグラフを表示します。

このコードは、地球と月の間の引力による運動をシミュレートし、月の楕円軌道を地球の周りにプロットしています。

結果解説

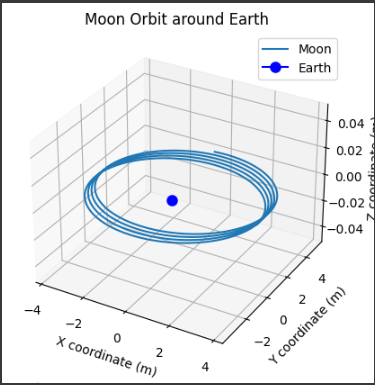
このグラフは、地球と月の間の万有引力を考慮した際の月の軌道を3Dで表現したものです。

青い点が地球を表し、月の軌道がその周りを回る様子が示されています。
地球は固定された位置にあり、月はその周りを楕円軌道で動いています。

月の軌道は、地球に引かれる重力によって決まります。
月が地球から遠ざかるときには引力が弱まり、近づくときには引力が強くなります。
その結果、月は楕円軌道を描きます。

この3Dグラフは、地球を中心に月が回転しながら地球の周りを周回する様子を視覚的に表現しています。
月の軌道が立体的に示されており、空間内での運動がわかりやすくなっています。