多変数関数の3次元グラフ化
多変数関数を使用した例を提供します。
以下のコードは、多変数関数 $ (z = f(x, y)) $の計算と3Dサーフェスプロットを示しています。
この例では、多変数関数$ (z) $を計算し、3Dサーフェスプロットで可視化します。
使用する関数は$ (z = \sin(\sqrt{x^2 + y^2}) / (\sqrt{x^2 + y^2} + 1)) $です。
1 | import numpy as np |
このコードは、$ (z = \frac{\sin(\sqrt{x^2 + y^2})}{\sqrt{x^2 + y^2} + 1}) $という複雑な多変数関数を計算し、3Dサーフェスプロットで可視化します。
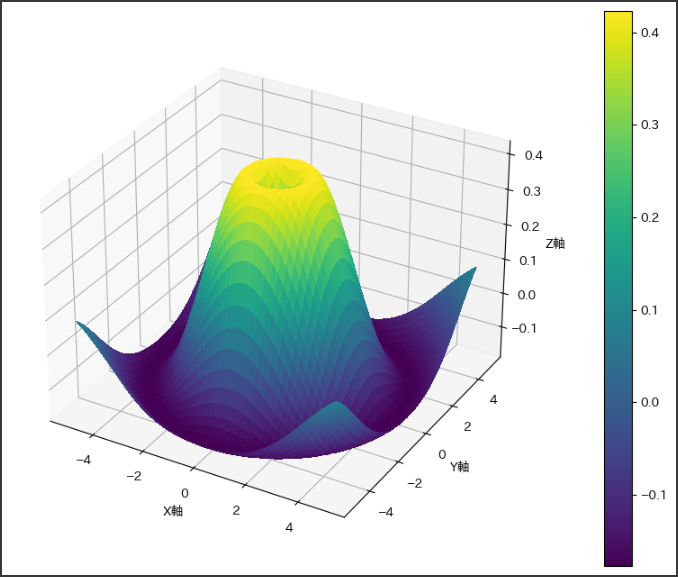
このプロットは、複雑な関数の3D表現を示しています。
必要に応じて、異なる関数やプロットスタイルを試すことができます。
ソースコード解説
このPythonソースコードは、3次元の複雑なグラフを作成し、matplotlibとNumPyを使用してそれを表示するものです。
以下はソースコードの詳細な説明です。
1. import numpy as np:
NumPyライブラリをインポートし、npという別名で使用できるようにします。
NumPyは数値計算のためのPythonライブラリで、多次元配列や数学関数のサポートが含まれています。
2. import matplotlib.pyplot as plt:
matplotlibライブラリをインポートし、pltという別名で使用できるようにします。
matplotlibはグラフを描画するためのPythonライブラリで、pyplotモジュールを使います。
3. from mpl_toolkits.mplot3d import Axes3D:
mpl_toolkits.mplot3dからAxes3Dをインポートします。
これは、3次元プロットを作成するために必要なモジュールです。
4. import japanize_matplotlib:
japanize_matplotlibをインポートし、日本語のテキストをmatplotlibのプロット内で正しく表示するためのライブラリです。
5. x = np.linspace(-5, 5, 100):
xという変数に、-5から5までの範囲を100の等間隔に区切った値が配列として格納されます。
この範囲と間隔は、x軸の値を指定します。
6. y = np.linspace(-5, 5, 100):
yという変数に、xと同様に-5から5までの範囲を100の等間隔に区切った値が格納されます。
この範囲と間隔は、y軸の値を指定します。
7. x, y = np.meshgrid(x, y):
xとyの値を使用して、2つの2D配列 x と y を生成します。
これらは後で3Dプロットを作成するために使用されます。
8. z = np.sin(np.sqrt(x**2 + y**2)) / (np.sqrt(x**2 + y**2) + 1):
多変数関数$ (z = f(x, y)) $の計算を行います。
ここでは、$ (z) は (x) $と$ (y) $の関数として、$(z = \frac{\sin(\sqrt{x^2 + y^2})}{\sqrt{x^2 + y^2} + 1}) $として計算されます。
9. fig = plt.figure(figsize=(10, 8)):
3Dプロットを含む新しい図を作成します。figsizeパラメータは、図のサイズを指定します。
10. ax = fig.add_subplot(111, projection='3d'):
図に3Dサブプロットを追加します。projection='3d'を指定して、3Dプロットを作成できるようにします。
11. surf = ax.plot_surface(x, y, z, cmap='viridis', linewidth=0, antialiased=False):
3Dサーフェスプロットを作成します。x、y、および z はプロットするデータです。cmap='viridis'はカラーマップを指定し、linewidth=0はプロットの線幅をゼロに設定し、antialiased=Falseはアンチエイリアスを無効にします。
12. fig.colorbar(surf, ax=ax, pad=0.1):
カラーバーをプロットに追加します。pad=0.1はカラーバーの位置を調整するためのパディングです。
13. ax.set_xlabel('X軸'), ax.set_ylabel('Y軸'), ax.set_zlabel('Z軸'):
X、Y、およびZ軸のラベルを設定します。
14. plt.show():
グラフを表示します。
