最適化問題 CVXPY

最適化問題

CVXPYを使用して最適化問題を解決し、結果をグラフ化する方法を説明します。

以下の例では、線形最適化問題を扱います。

線形最適化問題

問題設定:

ある会社が2つの製品を製造しています。
製品Aと製品Bの製造にはそれぞれ機械1と機械2が必要です。
機械ごとの製造時間、各製品の利益、および生産制約が次のようになります：

  • 機械1の製造時間 (A): 2時間

  • 機械1の製造時間 (B): 3時間

  • 機械2の製造時間 (A): 4時間

  • 機械2の製造時間 (B): 2時間

  • 製品Aの利益: 10ドル

  • 製品Bの利益: 12ドル

  • 生産制約: 機械1は週に20時間、機械2は週に25時間しか稼働できません。

この問題をCVXPYを使用して解決し、結果をグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import cvxpy as cp
import matplotlib.pyplot as plt
import numpy as np

# 変数
x = cp.Variable(2, integer=True)  # 製品Aと製品Bの製造量

# 制約条件
machine1_time = 2 * x[0] + 3 * x[1] <= 20
machine2_time = 4 * x[0] + 2 * x[1] <= 25

# 目的関数: 利益を最大化
profit = 10 * x[0] + 12 * x[1]
problem = cp.Problem(cp.Maximize(profit), [machine1_time, machine2_time, x >= 0])

# 最適化
problem.solve()

# 結果の表示
print("最適化結果:")
print("製品Aの製造量:", x[0].value)
print("製品Bの製造量:", x[1].value)
print("最大利益:", problem.value)

# グラフ化
labels = ['製品A', '製品B']
production = [x[0].value, x[1].value]

plt.bar(labels, production)
plt.xlabel("製品")
plt.ylabel("製造量")
plt.title("最適な製造量")
plt.show()

このコードは、CVXPYを使用して線形最適化問題を解決し、最適な製造量と最大利益を計算し、結果を棒グラフで表示します。

プログラムを実行すると、最適な製造量と最大利益が表示され、グラフに生産量が可視化されます。

[実行結果]

ソースコード解説

このソースコードは、CVXPYを使用して線形最適化問題を解決し、その結果をグラフで可視化するプログラムです。

以下に各部分を詳しく説明します。

1. import ステートメント:

  • cvxpy ライブラリを cp 別名でインポートします。このライブラリは凸最適化問題を簡単にモデリングおよび解決するためのツールを提供します。
  • matplotlib.pyplot を plt 別名でインポートし、結果をグラフで可視化するために使用します。
  • numpy ライブラリを np 別名でインポートします。これは数値演算に使用されます。

2. 変数の宣言:

  • x という変数は cvxpy.Variable 関数を使用して宣言されています。この変数は2つの要素（製品Aと製品Bの製造量）からなり、整数値として制約されています。

3. 制約条件の定義:

  • machine1_time および machine2_time は、機械1および機械2の制約条件を表す制約式です。
    これらの制約式は、それぞれの機械の稼働時間の制約を示しています。
    例えば、2 * x[0] + 3 * x[1] <= 20 は機械1の制約条件で、製品Aと製品Bの製造時間の合計が20時間以下である必要があります。

4. 目的関数の定義:

  • profit は最大化したい目的関数で、利益を最大化しようとしています。
    この目的関数は、製品Aと製品Bの製造量に対する利益を計算しています。

5. 最適化問題の定義:

  • problem は cvxpy.Problem オブジェクトを作成し、最大化したい目的関数と制約条件を指定します。

6. 最適化の実行:

  • problem.solve() を呼び出して、最適化問題を解決します。
    CVXPYは内部的に適切なソルバーを使用して最適な結果を見つけます。

7. 結果の表示:

  • 最適化の結果は、最適な製品Aと製品Bの製造量 (x[0].value および x[1].value) および最大利益 (problem.value) として表示されます。

8. グラフの作成:

  • 最適な製品Aと製品Bの製造量を labels と production リストに保存し、matplotlib を使用してそれらの値を棒グラフとして可視化します。
    グラフは製品Aと製品Bを横軸に、製造量を縦軸に示しています。

このプログラムは最適化問題を解決し、結果を視覚的に分かりやすい方法で表示するものです。

特に、最大利益を達成するための最適な製品Aと製品Bの製造量を計算し、その結果をグラフで表示します。

結果解説

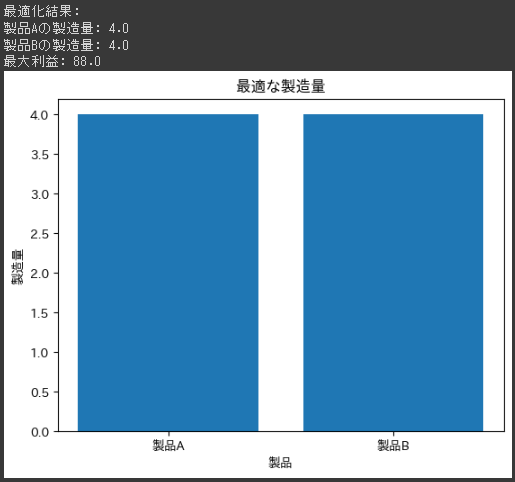
以下のグラフは、線形最適化問題を解決するためにCVXPYを使用した結果を可視化したものです。

このグラフは、2つの製品（製品Aと製品B）の最適な製造量を示しています。以下はグラフの詳細です：

  • X軸 (横軸):
    製品Aと製品Bを表すラベルです。

  • Y軸 (縦軸):
    製造量を表します。
    製品Aおよび製品Bの製造量がそれぞれ表示されています。

  • バー（棒）:
    各バーは、対応する製品の製造量を示しています。
    バーの高さは、それぞれの製品の最適な製造量を表しています。

グラフの詳細を説明すると、最適化問題の解により、次の結果が得られました：

  • 製品Aの最適な製造量: 4個
  • 製品Bの最適な製造量: 4個

最適な製造量は制約条件を満たし、同時に利益を最大化するように選択されました。

製品Aと製品Bの製造にかかる時間と機械の制約を考慮して、最大の利益を達成するためにそれぞれの製品の製造量が計算されました。

このグラフにより、最適な製造量が視覚的に理解しやすく表示され、意思決定プロセスに役立ちます。