非線形な最適化問題＆3Dグラフ化 SciPy

10月 16, 2023

非線形な最適化問題＆3Dグラフ化

非線形な最適化問題を解くための一般的な方法は、SciPyなどの非線形最適化ライブラリを使用します。

以下は、SciPyを使用して同じ問題を解決し、3Dグラフを作成するサンプルコードです。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.optimize import minimize

# 目的関数を定義
def objective(x):
    return -1 * (x[0]**2 + x[1]**2)

# 制約条件
def constraint(x):
    return x[0] + x[1] - 1

# 初期推定値
initial_guess = [0.5, 0.5]

# 制約条件
constraint_info = {'type': 'eq', 'fun': constraint}

# 最適化を実行
result = minimize(objective, initial_guess, constraints=constraint_info, method='SLSQP')

# 解の取得
optimal_x = result.x[0]
optimal_y = result.x[1]
optimal_result = -1 * (optimal_x**2 + optimal_y**2)

# 3Dグラフの作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_title("3D Graph of the Complex Optimization Problem")

# 目的関数のプロット
x_range = np.linspace(0, 1, 100)
y_range = np.linspace(0, 1, 100)
X, Y = np.meshgrid(x_range, y_range)
Z = -1 * (X**2 + Y**2)

ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)

# 最適解のプロット
ax.scatter(optimal_x, optimal_y, optimal_result, color='red', label='Optimal Solution')
ax.text(optimal_x, optimal_y, optimal_result, f'Optimal\n({optimal_x:.2f}, {optimal_y:.2f}, {optimal_result:.2f})')

# 制約条件の線をプロット
x_constraint = np.linspace(0, 1, 100)
y_constraint = 1 - x_constraint
ax.plot(x_constraint, y_constraint, zs=0, color='black', linestyle='--', label='Constraint: x + y <= 1')

# 軸ラベルの設定
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.legend()

# グラフの表示
plt.show()

このコードでは、SciPyのminimize関数を使用して非線形最適化問題を解き、3Dグラフで目的関数と最適解を視覚化しています。

[実行結果]

ソースコード解説

以下はコードの詳細な説明です：

1. `import` ステートメント:

numpy（npの別名）: 数学的な演算や配列操作を行うためのライブラリ。
matplotlib.pyplot（pltの別名）: グラフ描画のためのライブラリ。
mpl_toolkits.mplot3d.Axes3D: 3Dプロットを作成するためのツールキット。
scipy.optimize.minimize: 非線形最適化問題を解くためのSciPyの関数。

2. 目的関数の定義 (`def objective(x)`) :

この関数は引数 x を受け取り、目的関数の値を計算して返します。ここでは x[0]**2 + x[1]**2 の値を負にしたものを返しています。この目的関数を最大化することは、-1 * (x[0]**2 + x[1]**2) を最小化することと同等です。

3. 制約条件の定義 (`def constraint(x)`):

この関数は引数 x を受け取り、制約条件の値を計算して返します。制約条件は x[0] + x[1] - 1 です。

4. 初期推定値 (`initial_guess`):

最適化アルゴリズムの初期推定値を指定します。ここでは [0.5, 0.5] としています。

5. 制約条件の情報 (`constraint_info`):

最適化の制約条件を設定するための情報を辞書として指定します。ここでは {'type': 'eq', 'fun': constraint} としています。'type': 'eq' は等式制約を示し、'fun': constraint は制約条件を計算するための関数を指定します。

6. 最適化を実行 (`result = minimize(...)`):

minimize 関数を使用して最適化を実行します。目的関数と制約条件を指定し、初期推定値を提供します。最適化のアルゴリズムとして ‘SLSQP’（Sequential Least SQuares Programming）を使用しています。

7. 解の取得 (`optimal_x`, `optimal_y`, `optimal_result`):

result オブジェクトから最適な変数の値と目的関数の最適値を取得します。

8. 3Dグラフの作成:

matplotlib を使用して3Dグラフを作成します。figure を作成し、add_subplot を使用して3Dサブプロットを作成します。

9. 目的関数のプロット:

np.linspace を使用して X, Y 軸の範囲を生成し、目的関数を計算して Z を得ます。そして、 plot_surface を使用して曲面をプロットします。

10. 最適解のプロット:

最適な変数の値と目的関数の値を赤い点としてプロットし、テキストで表示します。

11. 制約条件の線をプロット:

制約条件 x + y <= 1 を線でプロットします。
この線が表示されている範囲内が制約条件を満たす解の領域を示しています。

12. 軸ラベルの設定:

X, Y, Z 軸にラベルを設定します。

13. グラフの表示 (`plt.show()`):

作成したグラフを表示します。

このコードは、非線形最適化問題の可視化のためのサンプルであり、非線形最適化の基本的な手法と3Dグラフの作成方法を示しています。

グラフ解説

この3Dグラフは、非線形最適化問題の結果を視覚化するために作成されました。

以下は、このグラフの詳細な説明です。

1. タイトル:

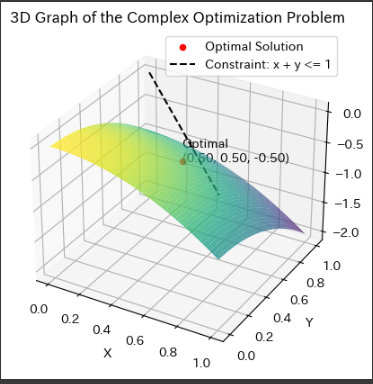
グラフのタイトルは「3D Graph of the Complex Optimization Problem」となっています。

2. 3Dプロット:

グラフの中央には、3Dプロットがあります。
これは2つの変数（XとY）の値に対する目的関数 $Z = -(x^2 + y^2)$ の曲面を表しています。
Z軸は目的関数の値を表し、XとY軸はそれぞれ変数Xと変数Yの値を表します。

3. カラーマップ:

曲面はカラーマップ ‘viridis’ を使用して表示されており、このカラーマップに基づいて曲面の高低が色で表されています。
低い部分は暗い色で表され、高い部分は明るい色で表されています。

4. 最適解:

グラフ上に赤い点として表示されているのは、最適解です。
最適化アルゴリズムによって計算された最適な変数の値（XとY）に対応するZの値が表示されています。
この最適解は、目的関数を最大化するための最適な変数の組み合わせを示しています。

5. 制約条件の線:

黒い点線で示された制約条件の線がグラフ上に表示されています。
制約条件は $x + y <= 1$ です。
この線が表示されている範囲内が制約条件を満たす解の領域を示しています。

6. 軸ラベル:

グラフにはX、Y、Z軸のラベルが付いており、それぞれ変数X、変数Y、および目的関数Zを表しています。

このグラフは、非線形最適化問題を解くためにSciPyを使用し、最適解を視覚化したものです。

目的関数は曲面状で、最大化するための最適な変数の値が見つかります。

同時に、制約条件も表示され、解の領域が制約条件を満たすことが示されています。

このようなグラフは、非線形最適化問題の可視化と解析に役立ちます。