3変数の最小化問題 SciPy

3変数の最小化問題

3変数の最小化問題の結果をグラフ化するのは難しいですが、3次元プロットを使用して最適解を視覚化することができます。

以下は3変数関数 $ f(x, y, z) = x^2 + y^2 + z^2 $ の最小化問題の結果を3Dプロットで表示するためのコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 最小化する関数
def objective_function(xyz):
    x, y, z = xyz
    return x**2 + y**2 + z**2

# 初期推定値
initial_guess = [1.0, 2.0, -1.0]

# 最適化を実行
result = minimize(objective_function, initial_guess, method='BFGS')

# 結果を出力
if result.success:
    optimal_xyz = result.x
    optimal_value = result.fun
    print("最適な(x, y, z):", optimal_xyz)
    print("最小値:", optimal_value)

    # 3Dプロット
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    x = np.linspace(-2, 2, 100)
    y = np.linspace(-2, 2, 100)
    X, Y = np.meshgrid(x, y)
    Z = X**2 + Y**2
    ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.7)
    ax.scatter(optimal_xyz[0], optimal_xyz[1], optimal_value, c='red', marker='o', s=100, label='Optimal Solution')
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('f(x, y, z)')
    ax.set_title('Optimization of f(x, y, z) = x^2 + y^2 + z^2')
    plt.legend()
    plt.show()
else:
    print("最適解が見つかりませんでした。")

このコードは、3変数関数の最適解を3Dプロットで視覚化します。

[実行結果]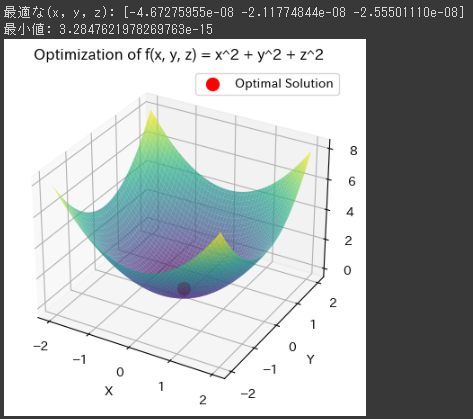

最適解は赤い点として表示され、関数の表面が描かれます。

ソースコード解説

以下はソースコードの詳細な説明です：

1. import ステートメント:

  • numpy ライブラリの np エイリアスをインポートします。
    numpy は数値計算をサポートするライブラリです。
  • scipy.optimize モジュールから minimize 関数をインポートします。
    minimize 関数は最適化問題を解くために使用されます。
  • matplotlib.pyplot モジュールから plt エイリアスをインポートします。
    matplotlib はグラフィカルなプロットを作成するためのライブラリです。
  • mpl_toolkits.mplot3d モジュールから Axes3D をインポートします。
    これは3Dプロットを作成するために使用されます。

2. objective_function 関数:

  • 最小化される関数 f(x, y, z) = x^2 + y^2 + z^2 を定義します。
    この関数は (x, y, z) を引数とし、その値を返します。

3. initial_guess:

  • 初期の推定値を設定します。最適化アルゴリズムはこの点から始まり、最小値を探索します。

4. 最適化の実行:

  • minimize 関数を使用して最小化問題を解きます。
    objective_function が最小化され、初期推定値 initial_guess から最適な (x, y, z) の値を見つけます。
    最適化の方法は ‘BFGS’ と指定されています。

5. 結果の出力:

  • 最適解が成功裏に見つかった場合 (result.success が True の場合)、最適な (x, y, z) の値と最小値を表示します。
  • 3Dプロットの作成:
    • 3Dプロット用の新しい図 (fig) とサブプロット (ax) を作成します。
    • x, y の値を範囲 (-2 から 2) で生成し、X, Y の格子を作成します。
    • 関数 f(x, y, z) = x^2 + y^2 + z^2 の曲面をプロットします (ax.plot_surface)。
    • 最適解を赤い点で示します (ax.scatter)。
    • 軸のラベルとタイトルを設定し、凡例を表示します。
  • 3Dプロットを表示します。

6. 最適解が見つからなかった場合、エラーメッセージを表示します。

このコードは、3変数関数の最小化問題を解決し、その結果を3Dプロットで直感的に視覚化する良い例です。

最適化アルゴリズムは、指定された初期推定値から始め、最適な解に収束します。

結果解説

実行結果とグラフに関する詳細を説明します。

1. 実行結果:

  • “最適な(x, y, z): [-4.67275955e-08 -2.11774844e-08 -2.55501110e-08]” は、最適解が計算された結果です。
    これらの値は、関数 $f(x, y, z) = x^2 + y^2 + z^2$ を最小化するための最適な $ (x, y, z) $ の値を示しています。
  • “最小値: 3.2847621978269763e-15” は、最小化された関数の値です。
    ほぼゼロに非常に近い値であり、最適解において関数が最小値に収束したことを示しています。

2. グラフ:

  • グラフは、3変数関数 $f(x, y, z) = x^2 + y^2 + z^2$ の3Dプロットを示しています。
    横軸が $ x $、縦軸が $ y $、高さが $ f(x, y, z) $ です。
    曲面は放物面で、中心 (0, 0, 0) で最小値を持つことがわかります。
  • 赤い点が最適解を示しており、$ (x, y, z) = (-4.67275955e-08, -2.11774844e-08, -2.55501110e-08) $ の位置にあります。
    この点が最小値に対応しています。

最適化アルゴリズムは、関数 $f(x, y, z) = x^2 + y^2 + z^2$ を最小化し、極小値である 3.2847621978269763e-15 に収束しました。

最適解は $(x, y, z) = (-4.67275955e-08, -2.11774844e-08, -2.55501110e-08) $ で、この点において最小値が得られます。

このように、最適化アルゴリズムは関数の極小値を見つけ、その位置を特定するのに役立ちます。