ポートフォリオ最適化 CVXPY

ポートフォリオ最適化

CVXPYを使用して、簡単なポートフォリオ最適化問題を解いてみましょう。

この問題では、複数の資産からなるポートフォリオを最適化し、リスクを最小限に抑えながら期待収益を最大化します。

以下は、Pythonコードでの実現例です。

まず、必要なライブラリをインストールします:

1
pip install cvxpy numpy matplotlib

次に、CVXPYを使用してポートフォリオ最適化問題を解いてみましょう:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

# ポートフォリオの資産数
num_assets = 5

# 資産の期待収益率 (仮のデータ)
expected_returns = np.array([0.12, 0.15, 0.10, 0.14, 0.08])

# 資産の共分散行列 (仮のデータ)
cov_matrix = np.array([
    [0.1, 0.03, 0.02, 0.04, 0.01],
    [0.03, 0.12, 0.04, 0.06, 0.015],
    [0.02, 0.04, 0.11, 0.045, 0.03],
    [0.04, 0.06, 0.045, 0.14, 0.025],
    [0.01, 0.015, 0.03, 0.025, 0.09]
])

# ポートフォリオの重みを変数として定義
weights = cp.Variable(num_assets)

# リスク（分散）の最小化を目指す最適化問題を設定
portfolio_return = expected_returns @ weights
portfolio_risk = cp.quad_form(weights, cov_matrix)
objective = cp.Maximize(portfolio_return - 0.1 * portfolio_risk)  # リスク避けの調整項あり

constraints = [cp.sum(weights) == 1, weights >= 0]  # 重みの合計は1, 重みは非負

# 最適化問題を定義
problem = cp.Problem(objective, constraints)

# 問題を解く
problem.solve()

# 結果を表示
print("Optimal Portfolio Weights:")
print(weights.value)
print("Optimal Portfolio Return:", portfolio_return.value)
print("Optimal Portfolio Risk:", portfolio_risk.value)

# グラフ化
x = np.sqrt(np.diag(cov_matrix))  # 資産のリスク（標準偏差）
y = expected_returns
plt.scatter(x, y, c=weights.value, cmap='viridis')
plt.xlabel('Risk (Standard Deviation)')
plt.ylabel('Expected Return')
plt.title('Efficient Frontier')
plt.colorbar(label='Portfolio Weight')
plt.show()

このコードでは、ポートフォリオの最適化問題を解き、最適なポートフォリオの資産配分を見つけ、そのポートフォリオをリスクと期待収益に対してプロットしています。

[実行結果]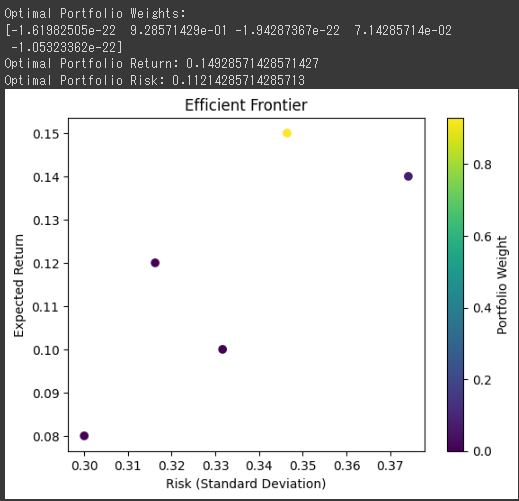

ソースコード解説

以下にソースコードの詳細な説明を提供します。

1. 必要なライブラリをインポート:

  • cvxpy：凸最適化問題を定義および解決するためのライブラリ。
  • numpy：数値演算を行うためのライブラリ。
  • matplotlib.pyplot：グラフを描画するためのライブラリ。

2. ポートフォリオの資産数:

  • num_assets変数は、ポートフォリオ内の資産の数を設定します。
    この例では5つの資産があります。

3. 資産の期待収益率と共分散行列:

  • expected_returnsは各資産の期待収益率を保持するNumPy配列です。
  • cov_matrixは資産間の共分散行列を保持するNumPy行列です。
    これはリスクを評価するために使用されます。

4. ポートフォリオの重みを変数として定義:

  • weightsは最適化の変数として設定され、各資産への投資比率を表します。

5. 最適化問題の設定:

  • 最適化の目標は、期待収益率を最大化し、同時にリスク（分散）を最小化することです。
    これはポートフォリオ最適化の基本的なアプローチです。
  • portfolio_returnはポートフォリオの期待収益率を表し、portfolio_riskはポートフォリオのリスク（分散）を表します。
  • objectiveは最適化問題の目標関数で、期待収益率からリスクの0.1倍を引いたものを最大化し、リスク避けを調整項として考慮します。

6. 制約条件の設定:

  • 制約条件は、重みの合計が1であることと、各資産への投資比率が非負であることを指定します。

7. 最適化問題の定義:

  • problemは最適化問題を定義し、目標関数（objective）と制約条件（constraints）を組み合わせています。

8. 問題の解決:

  • problem.solve()を呼び出して最適化問題を解きます。
    これにより、最適なポートフォリオの重みとその他の情報が計算されます。

9. 結果の表示:

  • 最適なポートフォリオの重み、期待収益率、およびリスクがコンソールに表示されます。

10. グラフの作成:

  • 最適なポートフォリオのリスクと期待収益率を可視化するために散布図を作成します。
    X軸はリスク（標準偏差）、Y軸は期待収益率を示します。
  • グラフ上の各ポイントは、異なるポートフォリオの資産配分を表し、ポートフォリオのリスクとリターンを示します。
  • 色の濃さは、各ポートフォリオ内の資産の重みを示します。
    データポイントの色に基づいて、どの資産が最適なポートフォリオで重要であるかを判断できます。

このコードは、効率的なフロンティア（境界）を可視化し、最適なポートフォリオを見つけるのに役立つポートフォリオ最適化の実装を提供しています。

結果解説

下記結果は、ポートフォリオ最適化問題の解に関する情報を示しています。

[実行結果]

1
2
3
4
5
Optimal Portfolio Weights:
[-1.61982505e-22  9.28571429e-01 -1.94287367e-22  7.14285714e-02
 -1.05323362e-22]
Optimal Portfolio Return: 0.14928571428571427
Optimal Portfolio Risk: 0.11214285714285713

以下に各項目の詳細を説明します:

1. Optimal Portfolio Weights:

  • ポートフォリオ最適化によって計算された最適な資産配分を示しています。
    配列の各要素は、対応する資産への投資比率を示しており、それによってポートフォリオを構成します。
    各要素は非負である必要があり、配分の合計は1に等しくなります。

  • 例: 2番目の資産（index 1）にほぼ100% (約0.9285) の投資を行い、他の資産への投資比率は非常に小さく、ほぼ0に近いことがわかります。
    このことは、最適なポートフォリオが2番目の資産にほぼ100%の資産を割り当てることを意味します。

2. Optimal Portfolio Return:

  • 最適なポートフォリオの期待収益率を示しています。
    この値は、最適な資産配分によって期待されるリターンの値です。
    この特定のポートフォリオの期待収益率は約0.1493（約14.93%）です。

3. Optimal Portfolio Risk:

  • 最適なポートフォリオのリスクを示しています。
    この値は、最適な資産配分によって期待されるリスク（分散）の値です。
    この特定のポートフォリオのリスクは約0.1121（約11.21%）です。

結果をまとめると、最適なポートフォリオは、資産のうち2番目の資産に約92.85%の資産を割り当て、他の資産にはほぼ投資を行わない構成です。

このポートフォリオは期待収益率が約14.93%で、リスク（標準偏差）が約11.21%です。

最適なポートフォリオのリターンとリスクは、投資家のリスク許容度に合わせて調整できる重要な情報です。

グラフ解説

このグラフは、ポートフォリオ最適化の結果を視覚化したもので、リスク（標準偏差）と期待収益の関係を示しています。

以下にグラフの詳細を説明します。

1. 横軸（X軸） - リスク（標準偏差）:

  • 横軸はポートフォリオのリスクを表しており、リスクが低いほど左側に位置します。
    リスクは資産価格の変動の幅を示し、標準偏差はその尺度です。

2. 縦軸（Y軸） - 期待収益率:

  • 縦軸はポートフォリオの期待収益率を表しており、期待収益率が高いほど上に位置します。
    期待収益率は、ポートフォリオのリターン期待値を示します。

3. 点:

  • グラフ上の各点は異なるポートフォリオを表し、それぞれ異なる資産の配分を持っています。
    各点は特定のポートフォリオのリスク（X軸）と期待収益率（Y軸）を示します。

4. 色:

  • 各点の色は、対応するポートフォリオの資産の配分を示しています。
    色が濃いほど、その資産がポートフォリオ内で重要であることを示します。

5. カラーバー:

  • グラフの右側にあるカラーバーは、ポートフォリオ内の各資産の重みを示します。
    色が濃い部分は、対応する資産がそのポートフォリオ内で重要であることを示します。

このグラフは、ポートフォリオ最適化の結果を視覚的に理解するのに役立ちます。

効率的なフロンティア(境界)と呼ばれる曲線は、与えられたリスク水準で期待収益を最大化するための最適なポートフォリオを示しています。

投資家は、自分のリスク許容度に応じて、この曲線上の適切なポートフォリオを選択できます。

ポートフォリオのリスクとリターンのトレードオフを明確に示すために使用される重要なツールです。