機械学習 scikit-learn

機械学習

簡単な機械学習タスクのデモを行います。

ここでは、サポートベクトルマシン（Support Vector Machine, SVM）を使用してデータの分類を行う例を示します。

まず、必要なライブラリをインポートします。

1
2
3
4
5
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt

次に、サンプルデータセットを生成します。

1
X, y = make_classification(n_samples=100, n_features=2, n_classes=2, n_clusters_per_class=1, n_redundant=0, random_state=42)

データをトレーニングセットとテストセットに分割します。

1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

SVMモデルをトレーニングします。

1
2
svm = SVC(kernel='linear')
svm.fit(X_train, y_train)

トレーニングしたモデルを使用してテストデータを予測します。

1
y_pred = svm.predict(X_test)

予測の精度を評価します。

1
2
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')

最後に、データと決定境界をプロットして可視化します。

1
2
3
4
5
6
7
8
9
10
11
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50), np.linspace(ylim[0], ylim[1], 50))
Z = svm.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], linestyles=['--', '-', '--'])
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

このデモでは、生成したデータセットを使用してSVMモデルをトレーニングし、予測の精度を評価し、データと決定境界を可視化しています。

データやモデルのパラメータを調整して異なる実験を行うことができます。

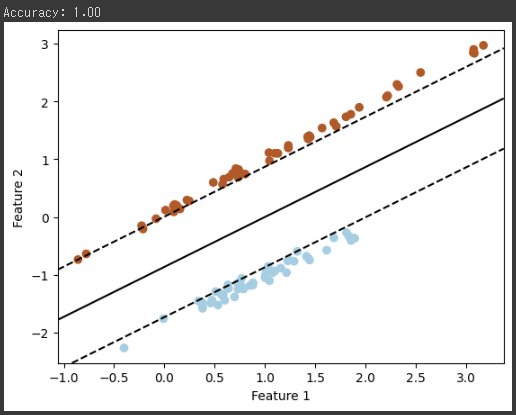
グラフ解説

このグラフは2つの特徴量を持つデータセットの散布図と、SVMによって学習された決定境界を表示しています。

以下に各要素の説明を提供します。

1. 散布図:

グラフの背景に表示されている点は、データセットの各サンプルを表しています。
データセットは2つのクラスからなり、各クラスのサンプルは異なる色で表示されています。
一方のクラスは青で、もう一方のクラスはオレンジで表されています。

2. 決定境界:

黒い破線と黒い実線で表される領域がSVMによって学習された決定境界です。
この決定境界は、異なるクラスのサンプルを分離するために見つけられた最適な線です。
破線はマージンの外側のサポートベクトルに対応し、実線はマージンの内側のサポートベクトルに対応します。
マージンは決定境界と最も近いサポートベクトルとの距離です。

3. 特徴空間:

グラフの軸はデータの特徴量を表しており、Feature 1とFeature 2が表示されています。
決定境界がこれらの特徴量の空間でデータを分離しています。

このグラフは、SVMによる2クラスのデータの分離を示しており、クラスごとに異なる特徴量の組み合わせを使用して分離を行っています。

決定境界は最も近いサポートベクトルからの距離が最大になるように決定されており、これにより未知のデータに対する一般化が向上します。

SVMは非常に強力な分類アルゴリズムであり、データが線形分離可能でない場合にはカーネルトリックを使用して非線形分離を行うこともできます。

このグラフはSVMの基本的な概念を示しています。