回帰⑤ (予測結果を可視化)

前回記事で、単回帰モデルの構築と予測を行いました。

今回はその予測結果を可視化し、構築したモデルの精度評価を行います。

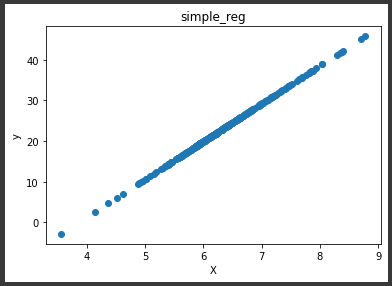
散布図（訓練データ）

訓練データの予測結果を散布図で表示します。

[Google Colaboratory]

plt.scatter(X_train, y_train_pred)
plt.xlabel("X")
plt.ylabel("y")
plt.title("simple_reg")
plt.show()

[実行結果]

上図のように直線で表される結果となりました。

単回帰は学習によって y = ax + b の傾き(a)と切片(b)を算出します。

学習によって導き出された式に、検証データの説明変数(x)を代入することで予測値(y)が算出されます。

そのため結果はこの直線上にのることになります。

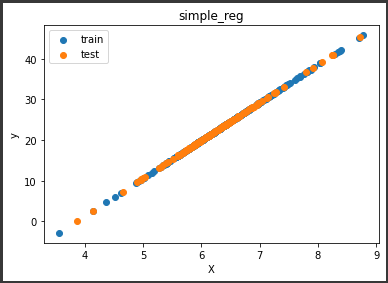
散布図（訓練データ・テストデータ）

訓練データの予測結果と合わせてテストデータの予測結果も散布図で表示します。

[Google Colaboratory]

plt.scatter(X_train, y_train_pred, label="train")
plt.scatter(X_test, y_test_pred, label="test")
plt.xlabel("X")
plt.ylabel("y")
plt.title("simple_reg")
plt.legend()
plt.show()

[実行結果]

テストデータの予測結果も、訓練データの予測結果と同じように直線状にのることが確認できました。

傾きと切片

この直線の傾き(a)と切片(b)は出力することができます。

[Google Colaboratory]

print(f"a = {simple_reg.coef_[0][0]}")
print(f"b = {simple_reg.intercept_[0]}")

[実行結果]

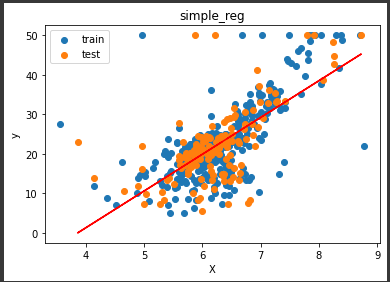
予測のプロット

実際の値と予測値を合わせて可視化します。

[Google Colaboratory]

plt.scatter(X_train, y_train, label="train")
plt.scatter(X_test, y_test, label="test")
plt.plot(X_test, y_test_pred, color="red")

plt.xlabel("X")
plt.ylabel("y")
plt.title("simple_reg")
plt.legend()
plt.show()

[実行結果]

赤い直線が回帰によって算出されたものです。

実測値と直線の距離が近いほど、モデルの精度が高いことになります。

上図より、多くは直線付近に分布していますが、一部は直線から大きく離れていることが分かります。

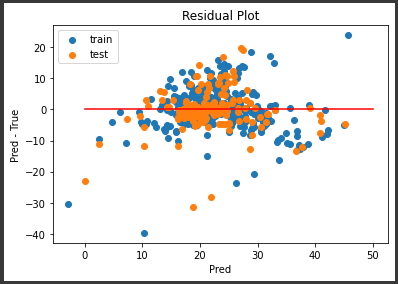
残差プロット

予測値と実測値の差に焦点をあてて可視化を行います。

残差プロットという手法を使います。

[Google Colaboratory]

plt.scatter(y_train_pred, y_train_pred - y_train, label="train")
plt.scatter(y_test_pred, y_test_pred - y_test, label="test")
plt.plot([0, 50], [0,0] ,color="red")
plt.xlabel("Pred")
plt.ylabel("Pred - True")
plt.title("Residual Plot")
plt.legend()
plt.show()

[実行結果]

残差プロットでは、予測値と実測値の差が0である理想的な状態（赤い線）から、実際の差がどれだけばらついているかという傾向を視覚的に把握することができます。

上図より、密集部分でも-10～20と範囲が広く、中には±20を超える外れ値もあり、ばらつきが大きい状態となっていることが分かります。