回帰⑥ (精度評価指標)

精度評価指標

予測値と実測値の差（誤差）の大きさを確認するために精度評価指標を使います。

精度評価指標は次のようなものがあります。

  • 平均絶対誤差（MAE：Mean Absolute Error）
    誤差の絶対値の総和の平均値。
    マイナス誤差の大きさを総和に反映させるため、絶対値を使用。
    値が0に近いほど誤差が小さい。
  • 平均二乗誤差（MSE：Mean Squared Error）
    誤差を二乗した値の総和の平均値。
    マイナス誤差の大きさを総和に反映させるために、二乗を使用。
    二乗しているため、MAE、RMSEよりも大きな値が出る傾向があり、外れ値の影響が大きく出やすい。
    値が0に近いほど誤差が小さい。
  • 二乗平均平方根誤差（RMSE：Root Mean Squared Error）
    MSEを1/2乗した値。
    値が0に近いほど誤差が小さい。
  • 決定係数（R2）
    MSEの尺度を取り直した値。
    0～1の範囲で値をとり、1に近いほど精度が高い。
    明確な基準はなくケースバイケースではあるが、0.7以上であれば比較的精度が高いと判断して良い。
  • 平均絶対パーセント誤差（MAPE：Mean Absolute Percentage Error）
    誤差の度合いを％で表したもの。

精度評価指標の算出（テストデータ）

テストデータの各精度評価指標を算出します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
import numpy as np

mae = mean_absolute_error(y_test, y_test_pred)
mse = mean_squared_error(y_test, y_test_pred)
rmse = np.sqrt(mse)
r2score = r2_score(y_test, y_test_pred)

print("テストデータスコア")
print(f"MAE = {mae}")
print(f"MSE = {mse}")
print(f"RMSE = {rmse}")
print(f"R2 = {r2score}")

[実行結果]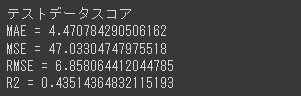

モデルの精度評価はテストデータに対する精度を見て行います。

理由は、機械学習モデルに求められるのは未知のデータを予測する性能（汎化性能）だからです。

（テストデータは未知のデータと見立てているため、学習には使用していません。）

精度評価指標の算出（訓練データ）

訓練データの各精度評価指標も算出します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
mae_train = mean_absolute_error(y_train, y_train_pred)
mse_train = mean_squared_error(y_train, y_train_pred)
rmse_train = np.sqrt(mse_train)
r2score_train = r2_score(y_train, y_train_pred)

print("訓練データスコア")
print(f"MAE = {mae_train}")
print(f"MSE = {mse_train}")
print(f"RMSE = {rmse_train}")
print(f"R2 = {r2score_train}")

[実行結果]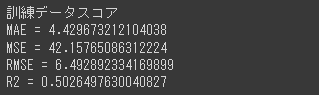

訓練データのスコアを出す理由は、モデルに過学習の傾向がないかどうかを確認するためです。

過学習とは、訓練データに対して過度に適合し、未知のデータへの予測精度が低くなってしまっている状態のことです。

訓練データのスコアが過度に高く、テストデータのスコアが低いといった場合は、そのモデルは過学習している可能性があります。

今回の回帰モデルでは過学習の傾向は見られませんでしたが、テストデータのR2スコアが0.43とでるなど、モデルの精度が高くない結果となりました、