Python × AI - 階層クラスタリング（最長距離法）

今回は最長距離法を使ってクラスタリングをします。

最長距離法は完全リンク法（complete_linkage）と呼ばれることもあり、各クラスタにおいて一番遠い点同士の距離をクラスタの距離とする方法です。

データセットの準備

前回と同様にscikit-learnのアヤメのデータセットを読み込みます。

比較しやすくするために、サンプル数を１０分の１に減らします。(4行目)

最後に散布図に表示します。(10行目)

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

X = load_iris().data[::10]
fig = plt.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 1, 1, title="iris")
plt.scatter(X[:, 0], X[:, 1])
for i, element in enumerate(X):
    plt.text(element[0]+0.02, element[1] + 0.02, i)
plt.show()

[実行結果]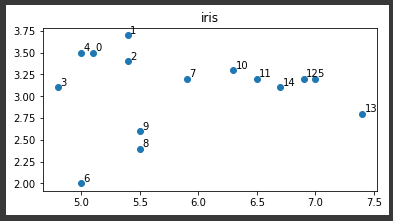

最長距離法とウォード法の比較

最長距離法とウォード法の両方でクラスタリングを行い、それぞれの樹形図を表示します。

最長距離法ではパラメータmethodに“complete”を指定(1行目)し、ウォード法では“ward”を指定(7行目)します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
Z = linkage(X, method="complete", metric="euclidean")
fig2, ax2 = plt.subplots(figsize=(6,3))
ax2 = dendrogram(Z)
fig2.suptitle("complete")
fig2.show()

Z = linkage(X, method="ward", metric="euclidean")
fig2, ax2 = plt.subplots(figsize=(6,3))
ax2 = dendrogram(Z)
fig2.suptitle("ward")
fig2.show()

[実行結果]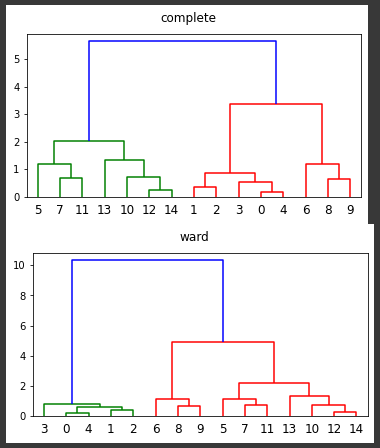

クラスタ数３として比較すると、まとまっている位置が変わっていますが同じように分類されているようです。

最長距離法は計算量が少なく、分類感度も比較的高いですが、拡散現象が生じることがあります。

拡散現象とはクラスターが大きくなるにつれ、他のデータと最長距離を多く持つようになり、次のクラスターの形成の候補に選ばれにくくなる現象です。