Python × AI - 階層クラスタリング（群平均法）

今回は群平均法を使ってクラスタリングをします。

群平均法は、クラスタ同士のすべての点同士の距離の平均をクラスタの距離とする方法です。

データセットの準備

前回と同様にscikit-learnのアヤメのデータセットを読み込みます。

比較しやすくするために、サンプル数を１０分の１に減らします。(4行目)

最後に散布図に表示します。(10行目)

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

X = load_iris().data[::10]
fig = plt.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 1, 1, title="iris")
plt.scatter(X[:, 0], X[:, 1])
for i, element in enumerate(X):
    plt.text(element[0]+0.02, element[1] + 0.02, i)
plt.show()

[実行結果]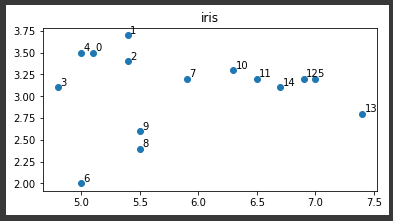

群平均法とウォード法の比較

群平均法とウォード法の両方でクラスタリングを行い、それぞれの樹形図を表示します。

群平均法ではパラメータmethodに“average”を指定(1行目)し、ウォード法では“ward”を指定(7行目)します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
Z = linkage(X, method="average", metric="euclidean")
fig2, ax2 = plt.subplots(figsize=(6,3))
ax2 = dendrogram(Z)
fig2.suptitle("average")
fig2.show()

Z = linkage(X, method="ward", metric="euclidean")
fig2, ax2 = plt.subplots(figsize=(6,3))
ax2 = dendrogram(Z)
fig2.suptitle("ward")
fig2.show()

[実行結果]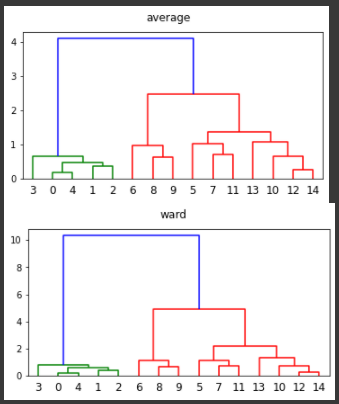

距離の違いはありますが、同じクラスタリング結果となりました。

群平均法は、鎖効果や拡散現象を起こさないため、ウォード法と同様に用いられることが多い手法です。