Python × AI [最適なクラスタ数を探索] - エルボー法

k-means法を使う際の問題点の１つは、クラスタ数を指定しなければならないことです。

今回はエルボー法という方法で最適なクラスタ数を探索していきます。

エルボー法とは

クラスタリングの性能を数値化するには、クラスタ内の残差平方和(SSE)という指標を用います。

エルボー法は、クラスタの数を変えながら残差平方和(SSE)を計算し結果を図表することで適切なクラスタ数を推定する手法です。

サンプルデータの作成と可視化

サンプルデータを作成し、可視化を行います。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.datasets import make_blobs
from sklearn import cluster, preprocessing
# サンプルデータの作成
X,y=make_blobs(n_samples=150,       # サンプル点の総数
               n_features=2,        # 説明変数（次元数）の指定
               centers=3,           # クラスタの個数
               cluster_std=0.5,     # クラスタ内の標準偏差
               shuffle=True,        # サンプルをシャッフル
               random_state=0)      # 乱数生成器の状態
# データを標準化（スケールを合わせるため）
sc=preprocessing.StandardScaler()
X_norm=sc.fit_transform(X)
x=X_norm[:,0]
y=X_norm[:,1]
plt.figure(figsize=(10,3))
plt.scatter(x,y)
plt.show

[実行結果]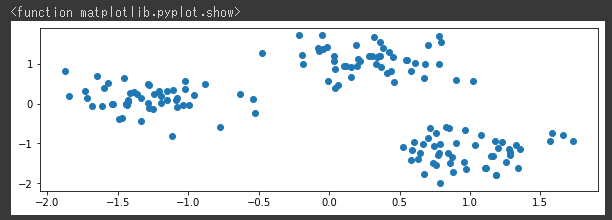

３つのグループに分かれたデータを作成することができました。

残差平方和(SSE)を算出

k-meansにてクラスタ数を1から10までのループし残差平方和(SSE)=km.inertia_を算出しリストに格納します。

残差平方和(SSE)が小さいほど歪みのない良いモデル（クラスタリングがうまくいっているモデル）ということになります。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
distortions = []
for i  in range(1,11): 
    km = KMeans(n_clusters=i,
                n_init=10,
                max_iter=300,
                random_state=0)
    km.fit(X_norm)
    distortions.append(km.inertia_)

plt.plot(range(1,11),distortions,marker="o")
plt.xticks(range(1,11))
plt.xlabel("Number of clusters")
plt.ylabel("Distortion")
plt.show()

[実行結果]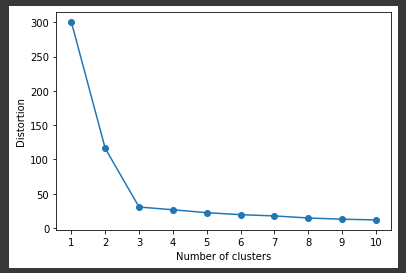

この図がエルボー図と呼ばれます。

クラスタ数3までは、残差平方和(SSE)が減少しクラスタ数4以降はほぼ横ばいとなっています。

エルボー法では、今回のデータにおいてのクラスタ数3のように急激に変化している点を最適なクラスタ数として選択します。

最適なクラスタ数でのクラスタリング

エルボー法で最適クラスタ数と導き出された3を指定して、クラスタリングを行います。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
km = KMeans(n_clusters=3,
                n_init=10,
                max_iter=300,
                random_state=0)
z_km=km.fit(X_norm)    
plt.figure(figsize=(10,3))
plt.scatter(x,y, c=z_km.labels_)
plt.scatter(z_km.cluster_centers_[:,0],z_km.cluster_centers_[:,1],s=250, marker="*",c="red")
plt.show

[実行結果]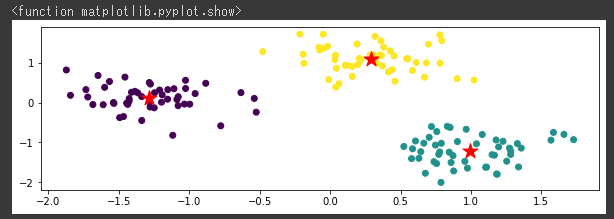

きれいに３つのクラスタ（グループ）に分類することができました。

エルボー法を用いることで、数値として根拠を持ったクラスタ数の探索が可能になることが分かりました。

ただ、かなり明確に分かれたデータでないとエルボー図はなだらかな曲線を描き最適なクラスタ数を判定するのが難しいため、万能な手法ではありません。

次回は別の方法でクラスタ数を探索していきます。