ニューラルネットワークで画像認識

ニューラルネットワークで手書き文字の認識をします。有名なMNIST(エムニスト)です。
まず必要なモジュールをインポートします。

1
2
3
4
# モジュール読み込み
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds

MNISTデータを読み込み、確認のために画像として表示してみます。

1
2
3
4
5
6
7
8
9
10
11
# MNISTデータの読み込み
MNIST = ds.load_digits()
xdata = MNIST.data.astype(np.float32)
tdata = MNIST.target.astype(np.int32)

# 配列の形を確認
D, N = xdata.shape

# 画像データの表示
plt.imshow(xdata[0,:].reshape(8, 8))  # 1列に並んだデータを8行8列に変換
plt.show()

結果

データ分割関数を定義し、実行します。今回、訓練データと学習データはちょうど半分ずつにしています。

1
2
3
4
5
6
7
8
9
10
11
# データ分割関数
def data_divide(Dtrain, D, xdata, tdata):
    index = np.random.permutation(range(D))
    xtrain = xdata[index[0:Dtrain],:]
    ttrain = tdata[index[0:Dtrain]]
    xtest = xdata[index[Dtrain:D],:]
    ttest = tdata[index[Dtrain:D]]
    return xtrain, xtest, ttrain, ttest

Dtrain = D // 2
xtrain, xtest, ttrain, ttest = data_divide(Dtrain, D, xdata, tdata)

chainerの宣言をします。

1
2
3
4
5
# chainerの宣言
import chainer.optimizers as Opt
import chainer.functions as F
import chainer.links as L
from chainer import Variable, Chain, config

ニューラルネットワークを作成し、ニューラルネットワークの関数を定義します。
また誤差と正解率の遷移を記録する変数を用意します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# ２層のニューラルネットワークを作成
C = tdata.max() + 1
NN = Chain(l1=L.Linear(N, 20), l2=L.Linear(20, C))

# ２層ニューラルネットワークの関数化
def model(x):
    h = NN.l1(x)
    h = F.relu(h)
    y = NN.l2(h)
    return y

# 最適化手法の設定
optNN = Opt.MomentumSGD()
optNN.setup(NN)

# 学習記録用エリア
train_loss = []
train_acc = []
test_loss = []
test_acc = []

最適化を行います。今回は200回学習を行います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 最適化
T = 200
for time in range(T):
    # 学習
    config.train = True
    optNN.target.zerograds()
    ytrain = model(xtrain)
    loss_train = F.softmax_cross_entropy(ytrain, ttrain)
    acc_train = F.accuracy(ytrain, ttrain)
    loss_train.backward()
    optNN.update()

    # テスト（検証）
    config.train = False
    ytest = model(xtest)
    loss_test = F.softmax_cross_entropy(ytest, ttest)
    acc_test = F.accuracy(ytest, ttest)

    # 結果の記録
    train_loss.append(loss_train.data)
    test_loss.append(loss_test.data)
    train_acc.append(acc_train.data)
    test_acc.append(acc_test.data)

グラフ表示用の関数を定義します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# グラフ表示関数
def show_graph(result1, result2, title, xlabel, ylabel, ymin=0.0, ymax=1.0):
    # 学習記録の表示(誤差)
    Tall = len(result1)
    plt.figure(figsize=(8, 6))
    plt.plot(range(Tall), result1, label='train')
    plt.plot(range(Tall), result2, label='test')
    plt.title(title)
    plt.xlabel(xlabel)
    plt.ylabel(ylabel)
    plt.xlim([0, Tall])
    plt.ylim(ymin, ymax)
    plt.legend()
    plt.show()

誤差と正解率の遷移をグラフ表示します。

1
2
3
# 誤差と正解率をグラフ表示
show_graph(train_loss, test_loss, 'loss function', 'step', 'loss_function', 0.0, 4.0)
show_graph(train_acc, test_acc, 'accuracy', 'step', 'accuracy')

結果

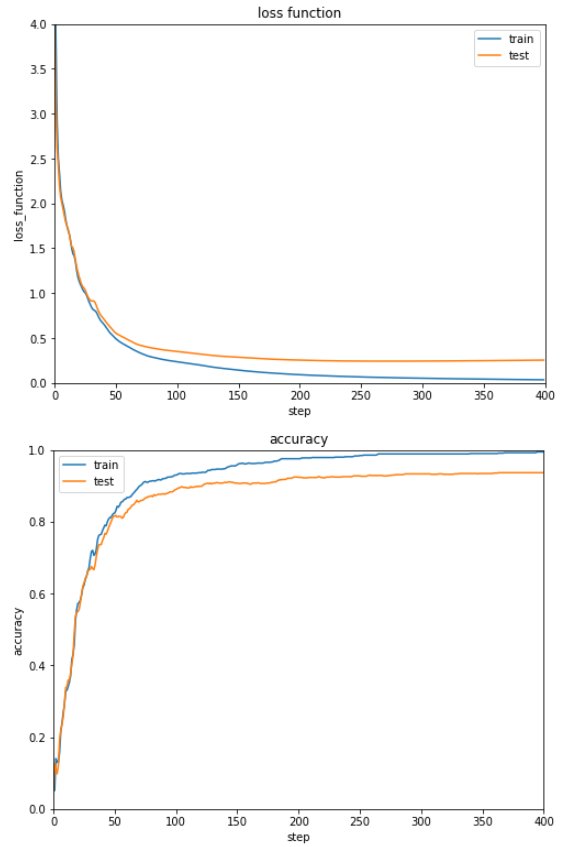
順調に誤差が減少し、正解率が上昇していることが見てとれます。
ただ正解率が９割そこそこなのが少々不満です。
非線形関数や最適化手法を変えて改善する余地はありそうです。

(Google Colaboratoryで動作確認しています。)