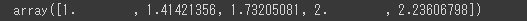NumPyには、切り捨て、切り上げ、四捨五入を行うメソッドが用意されています。

切り捨て

floor()メソッドを使うと、小数部を切り捨てて、値が小さい方の整数に変換にします。

[Google Colaboratory]

1
2
3
4

import numpy as np
x = np.array([-1.8, -1.4, -1.0, -0.6, -0.2, 0., 0.2, 0.6, 1.0, 1.4, 1.8])

np.floor(x)  # 切り捨て(値が小さい方の整数にする)

[実行結果]

trunc()メソッドを使うと、単純に小数部を切り捨てます。

[Google Colaboratory]

1

np.trunc(x)  # 切り捨て(小数部分を切り捨てる)

[実行結果]

切り上げ

ceil()メソッドを使うと、小数部を切り上げます。

[Google Colaboratory]

1

np.ceil(x)   # 切り上げ（大きい方の整数にする)

[実行結果]

四捨五入

round()メソッドを使うと、小数部を四捨五入します。

[Google Colaboratory]

1

np.round(x)  # 四捨五入

[実行結果]

around()メソッドを使うと、小数部を四捨五入します。

[Google Colaboratory]

1

np.around(x)  # 四捨五入

rint()メソッドを使うと、小数部を四捨五入します。

[実行結果]

[Google Colaboratory]

1

np.rint(x)

[実行結果]

0に近い方の整数

fix()メソッドを使うと、0に近い方向の整数に変換します。

[Google Colaboratory]

1

np.fix(x)     # 0に近いほうの整数をとる

[実行結果]

ラジアンと角度の相互変換

NumPyで実装されている三角関数系の関数は、基本的にラジアンを引数に設定します。

角度に π / 180 をかけるとラジアンに変換でき、ラジアンに 180 / π をかけると角度に変換できます。

NumPyにはこれらの変換処理を行う関数が用意されています。

• radians()、deg2rad()
  角度をラジアンに変換する。
• rad2deg()
  ラジアンを角度に変換する。

[Google Colaboratory]

1
2
3
4

import numpy as np
x = np.array([90, 180, 270], dtype = np.float)

np.radians(x)              # 角度をラジアンに変換

[実行結果]

[Google Colaboratory]

1

np.deg2rad(x)              # 角度をラジアンに変換

[実行結果]

[Google Colaboratory]

1

np.rad2deg(np.deg2rad(x))  # ラジアンを角度に変換

[実行結果]

逆関数

NumPyで、三角関数の逆関数は各関数名の頭に arc がつきます。

例えば arcsin は、y = sin(x) のときの x の値を x = arcsin(y) として求めることができます。

出力される値は、degree（度）ではなく radian（ラジアン） になります。

[Google Colaboratory]

1
2
3
4

import numpy as np
x = np.array([0.5, 1], dtype = np.float)

np.arcsin(np.sin(x)) # sinの逆関数

[実行結果]

[Google Colaboratory]

1

np.arccos(np.cos(x)) # cosの逆関数

[実行結果]

[Google Colaboratory]

1

np.arctan(np.tan(x)) # tanの逆関数

[実行結果]

NumPyにはサイン、コサイン、タンジェントを計算する関数が用意されています。

サイン

サインを計算するには sin() を使います。

引数には、degree（度）ではなく radian（ラジアン） を指定します。

[Google Colaboratory]

1
2
3
4

import numpy as np

x = np.array([0, 1], dtype = np.float)
np.sin(x)

[実行結果]

[Google Colaboratory]

1

np.sin(np.pi * 0.5)   # π/2のときのサインの値は1

[実行結果]

コサイン

コサインを計算するには cos() を使います。

引数には、degree（度）ではなく radian（ラジアン） を指定します。

[Google Colaboratory]

1

np.cos(x)

[実行結果]

[Google Colaboratory]

1

np.cos(np.pi * 0.5)    # 0になる

[実行結果]

タンジェント

タンジェントを計算するには tan() を使います。

引数には、degree（度）ではなく radian（ラジアン） を指定します。

[Google Colaboratory]

1

np.tan(x)

[実行結果]

[Google Colaboratory]

1

np.tan(np.pi * 0.5)    # 無限に発散する

[実行結果]

円周率

円周率を表す ndarray.pi も用意されています。

[Google Colaboratory]

1

np.pi  # 円周率

[実行結果]

ベクトルの累乗

NumPyで、累乗は power(配列, 指数) で求めることができます。

また、演算子の ** で求めることも可能です。

[Google Colaboratory]

1
2
3

import numpy as np
x = np.array([1, 2, 3, 4, 5], dtype = np.float)
np.power(x, 2)

[実行結果]

[Google Colaboratory]

1

x ** 2

[実行結果]

ベクトルの平方根

NumPyで、平方根は sqrt(x) で求めることができます。

[Google Colaboratory]

1
2

x = np.array([1, 2, 3, 4, 5], dtype = np.float)
np.sqrt(x)

[実行結果]

スカラー演算

線形代数では、大きさのみで表され、方向をもたない量のことをスカラーと言います。

つまり、0 や 1、2 などの連続しない独立した単一の値がスカラーです。

ベクトルは１次元配列なので、ベクトルに対してスカラー演算を行う場合、forなどで処理を繰り返す必要があります。

しかしndarrayオブジェクトとして作成したベクトル列は、ループを使わず一括して処理が行えます。

ブロードキャスト

NumPyでは、ブロードキャストという仕組みを使うことで、成分ごとの演算をまとめて行うことができます。

ブロードキャストを行うための条件は下記のいずれかの条件を満たした場合です。

• 次元が等しい。
• 一方のベクトルまたは行列がスカラーである。（スカラー演算）

スカラー演算のサンプル

ベクトルに対して四則演算子でスカラー演算を行うと、すべての要素に対して演算を行うことができます。

[Google Colaboratory]

1
2
3
4
5
6
7
8

import numpy as np

# ベクトルを作成
import numpy as np
x = np.array([1, 2, 3, 4, 5], dtype = np.float)

# 足し算
x + 20

[実行結果]

[Google Colaboratory]

1
2

# 引き算
x - 10

[実行結果]

[Google Colaboratory]

1
2

# 掛け算
x * 100

[実行結果]

[Google Colaboratory]

1
2

# 割り算
x / 2

[実行結果]

[Google Colaboratory]

1
2

# 割り算の結果を整数だけにする
x // 3

[実行結果]

[Google Colaboratory]

1
2

# 剰余
x % 3

[実行結果]

ベクトルに対してそれぞれのスカラー演算が行われていることが確認できました。

NumPyとは

NumPyは数値計算ライブラリで、Pythonがデータサイエンスの分野で注目されるのに貢献しています。

Pythonの仕様を踏まえつつ、高度な数値計算を高速に行えるように設計されていてコアな部分はC言語で実装されています。

配列の作成

線形代数では、要素を縦または横に一列に並べたものをベクトルと呼びます。

プログラミングでいうと１次元の配列のことです。

NumPyの配列（ベクトル）はndarrayクラスのオブジェクトとして表現され、arrayコンストラクタで作成します。

[Google Colaboratory]

1
2
3
4
5
6

import numpy as np

x = np.array([1, 2, 3, 4, 5],   # 配列要素
             dtype = np.float   # 実数型(float)にする
             )
print(x)

arrayコンストラクタの第１引数には、カンマで区切って要素を指定します。

第２引数には配列の型をdtypeで指定します。今回は小数を含む実数型としてnp.floatを指定しています。

[実行結果]

実数型のベクトル（１次元配列）を作成することができました。

Yield curve Analysis

利回り曲線分析では、連邦政府が一定期間お金を借りるのにどれだけの費用がかかるかを示し、長期金利と短期金利の関係を明らかにすることができます。

今後、インフレ率がどの程度になるか、どれだけの経済成長が見られるか、などの将来的な経済の予測を行うこともできます。

Yield curve Analysis - https://dash.gallery/dash-yield-curve/

Fifa Dashboard

Fifa DashboardのPlayer Comparisonダッシュボードを使うと、サッカー選手の特徴を容易に比較することができます。

Fifa Dashboard - https://dash.gallery/dash-fifa-dashboard/

左右のドロップダウンリストからサッカー選手を選ぶと、二人の選手の特徴がそれぞれ表示されます。

真ん中のレーダーチャートには２人の選手のパス／ドリブル／ディフェンス／シュート／足の速さ／フィジカルに関する評価が重ねて表示されます。

また下のテーブルには、プレイヤーの様々な情報（氏名、国籍、ポジション、年棒、スキル、ポテンシャルなど）も表示されます。

Dash Autonomous Driving

今回ご紹介するアプリでは、自動運転の様子をシミュレーションします。

自動運転車の走行から収集されたシーンを読み込み、センサーによるデータ(LIDAR、パスなど) と手動で注釈を付けたデータ(境界ボックス) の両方を表示します。

Dash Autonomous Driving Demo - https://dash.gallery/dash-avs-explorer/

ユーザインターフェース(UI)は、基本的なUIと高度なUIがあり、モードをクリックすることで切り替えができます。

どちらのユーザインターフェース(UI)も streetscape.gl を使用して作成されており、Dash コンポーネントとして利用できます。