半分全列挙
全パターンを列挙することができないようなサイズの問題でも、半分ならば全列挙を行うことができる ような場合があります。
このような場合、それぞれ半分ずつ全列挙されたものを組み合わせるという手法が有効なことがよくあります。
[問題]
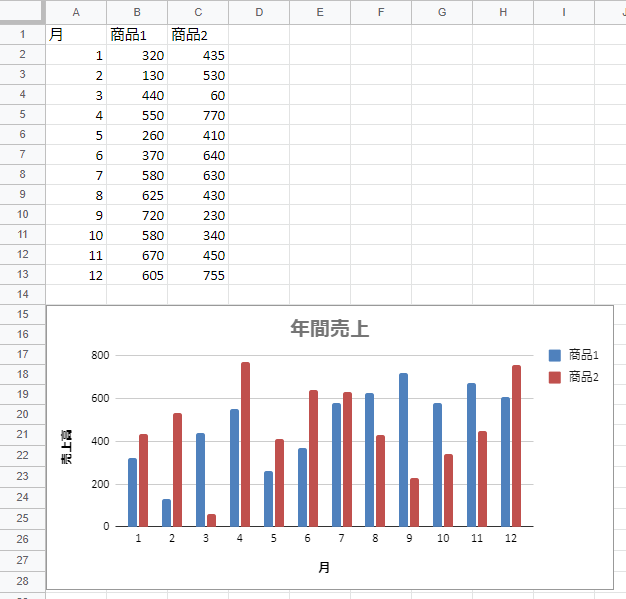
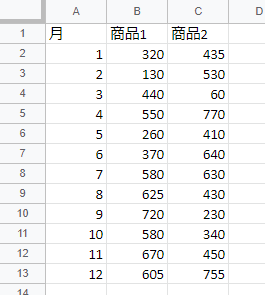
要素数nの整数のリストA、B、C、Dがあります。 各リストから1つずつ取り出したとき、その和が0となる ような 組み合わせの個数を求めなさい。 ただし、1つのリストに同じ値が複数個含まれている場合、 それらは異なるものとして数えます。
[条件]
・要素数は、1以上4000以下 ・リストの値の絶対値は、2の28乗以下
[解き方]
4つのリストからの取り出し方は全部で nの4乗通り もあるため、全てを調べることはできませんが、リストをABとCDという 半分ずつの組に分けて 考えることにより、効率的に解くことが可能になります。
2つのリストからの取り出し方は nの2乗通り しかないため、これならば全パターン列挙することができます。
リストAとリストBからそれぞれa,bを取り出したときに和を0にするには、リストCとリストDからの取り出し方 nの2乗通り 全てについて、その和を全て算出しておくことにより検索しやすくなります。
[Google Colaboratory]
1 | #--------入力例1---------------- |
[実行結果]
5
結果としては、組み合わせ数 5 だけが表示していますが、ソースを少し修正すると和が0になるときの組み合わせを表示することができます。
[組み合わせ]
①-45 30 42 -27 ②26 -46 -10 30 ③-32 30 56 -54 ④-32 77 -75 30 ⑤-32 -46 56 22
興味がある方は、組み合わせを表示するようにソースコードを修正してみてください。