飲食業の需要予測

飲食業の需要予測の例題をProphetを使用して解いてみましょう。

まず、仮想のデータセットを用意しましょう。

例えば、過去4年間のあるレストランの月間売上データを持っているとします。

以下にデータの例を示します：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

日付,売上
2022-01-01,1000
2022-02-01,1200
2022-03-01,1100
2022-04-01,1300
2022-05-01,1400
2022-06-01,1500
2022-07-01,1300
2022-08-01,1200
2022-09-01,1100
2022-10-01,1000
2022-11-01,1200
2022-12-01,1300
2023-01-01,1400
2023-02-01,1500
2023-03-01,1600
2023-04-01,1400
2023-05-01,1300
2023-06-01,1200
2023-07-01,1100
2023-08-01,1000
2023-09-01,1200
2023-10-01,1300
2023-11-01,1400
2023-12-01,1500
2024-01-01,1600
2024-02-01,1700
2024-03-01,1500
2024-04-01,1400
2024-05-01,1300
2024-06-01,1200
2024-07-01,1100
2024-08-01,1000
2024-09-01,1200
2024-10-01,1300
2024-11-01,1400
2024-12-01,1500
2025-01-01,1600
2025-02-01,1700
2025-03-01,1800
2025-04-01,1600
2025-05-01,1500
2025-06-01,1400
2025-07-01,1300
2025-08-01,1200
2025-09-01,1100
2025-10-01,1000
2025-11-01,1200
2025-12-01,1300

それでは、PythonのProphetライブラリを使用してこのデータセットで需要予測を行ってみましょう。

まず、Prophetライブラリがインストールされていない場合は、次のコマンドを使用してインストールします：

1

!pip install prophet

インストールが完了したら、以下のコードを使って進めます。

以下は、提供されたデータセットを使用してProphetを使った需要予測を行う例です：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import pandas as pd
from prophet import Prophet
import matplotlib.pyplot as plt

# データセットの定義
data = pd.read_csv('データセットのパス.csv')

# Prophet用にデータを準備する
data = data.rename(columns={'日付': 'ds', '売上': 'y'})

# Prophetモデルの作成
model = Prophet()

# データにモデルをフィットさせる
model.fit(data)

# 予測のための未来の日付を生成する
future_dates = model.make_future_dataframe(periods=12, freq='M')

# 予測を実行する
forecast = model.predict(future_dates)

# 予測結果をグラフ化する
model.plot(forecast, xlabel='Date', ylabel='Sales')
plt.title('Restaurant Demand Forecast')
plt.show()

この例では、まず必要なライブラリをインポートし、Prophetもインポートしています。

次にデータセットを読み込み、列名をProphetの予測モデルに合わせて変更しています。

その後、Prophetモデルを作成し、データにフィットさせ、予測のための未来の日付を生成します。

最後に、モデルを使用して未来の日付の売上を予測し、予測結果をグラフ化しています。

'データセットのパス.csv'の部分は、実際のデータセットファイルのパスに置き換えてください。

また、make_future_dataframeのperiodsパラメータを調整して、予測する未来の期間の数を指定することもできます。

ソースコード解説

以下、コードの各部分の詳細な説明です。

1. ライブラリのインポート:

1
2
3

import pandas as pd
from prophet import Prophet
import matplotlib.pyplot as plt

• pandas: データ操作や分析のためのPythonライブラリ。
• Prophet: Facebookが開発した時系列予測ライブラリ。このライブラリを使用して時系列モデルを構築し、予測を行う。
• matplotlib.pyplot: グラフを描画するためのPythonライブラリ。

2. データセットの読み込み:

1

data = pd.read_csv('データセットのパス.csv')

CSV形式のデータセットを読み込み、dataという名前のDataFrame（表形式のデータ構造）に格納しています。

3. データの準備:

1

data = data.rename(columns={'日付': 'ds', '売上': 'y'})

データのカラム名をProphetの予測モデルに合わせるために変更しています。
'日付'カラムは時系列の日付を表し、'売上'カラムは予測する対象の数値データ（売上）を表しています。

4. Prophetモデルの作成:

1

model = Prophet()

Prophetのモデルをインスタンス化します。
このモデルは、時系列データからトレンド、季節性、ホリデーエフェクトなどを学習し、予測を行うために使用されます。

5. モデルのデータへのフィッティング（適合）:

1

model.fit(data)

dataに格納されたデータを使用して、Prophetモデルに適合させます。
モデルはここでデータのトレンドや季節性を学習します。

6. 未来の日付の生成:

1

future_dates = model.make_future_dataframe(periods=12, freq='M')

予測を行うための未来の日付を生成します。
periodsで指定した期間（ここでは12ヶ月）分の日付を生成し、freqで頻度を’M’（月ごと）として指定しています。

7. 予測の実行:

1

forecast = model.predict(future_dates)

未来の日付に対して予測を実行し、forecastというDataFrameに予測結果を格納します。

8. 予測結果のグラフ化:

1
2
3

model.plot(forecast, xlabel='Date', ylabel='Sales')
plt.title('Restaurant Demand Forecast')
plt.show()

予測結果をグラフ化して表示します。
x軸には日付を、y軸には売上を表示します。
また、グラフのタイトルも設定されています。

このコードは、Prophetを使用して時系列データの売上予測を行い、その結果を可視化する一連の手順を示しています。

結果解説

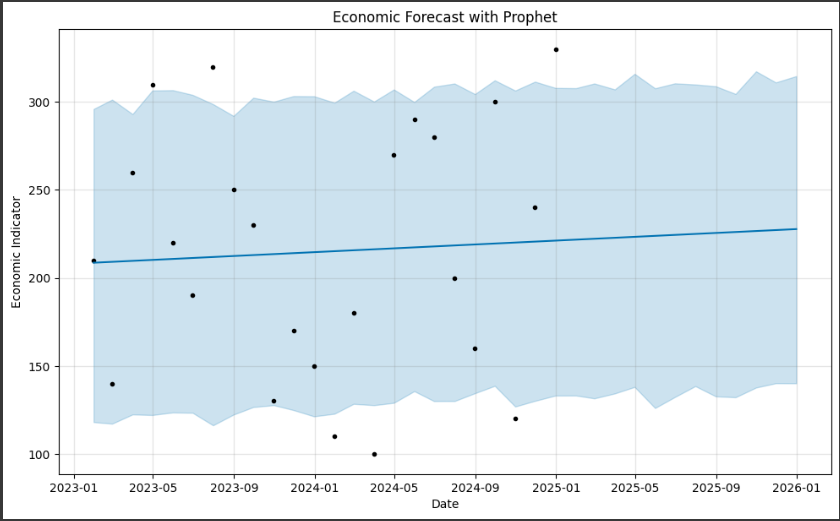
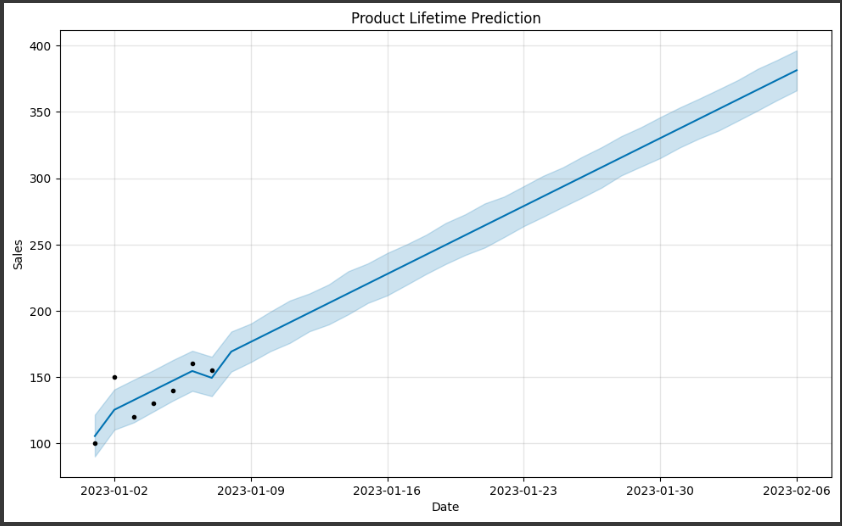
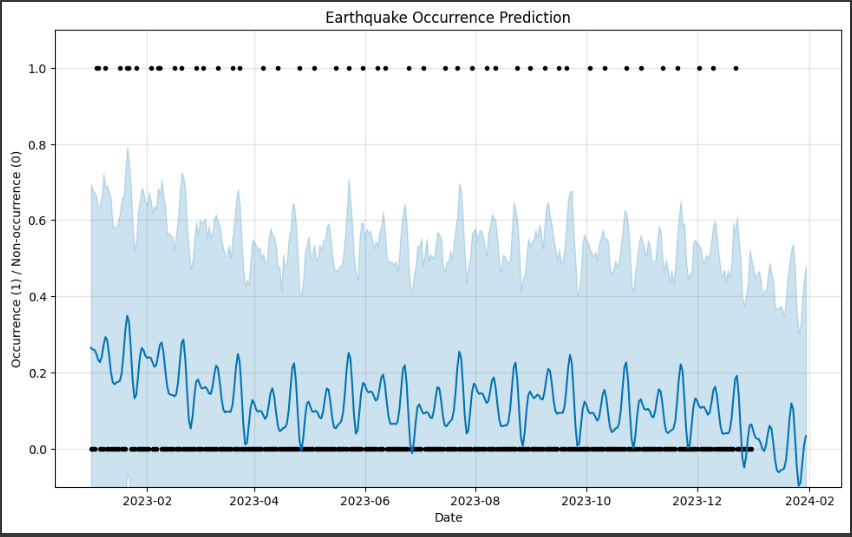
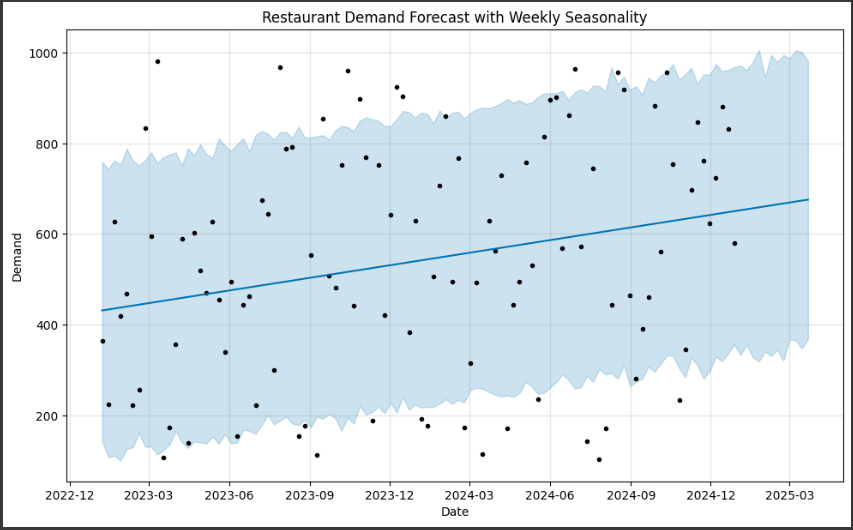
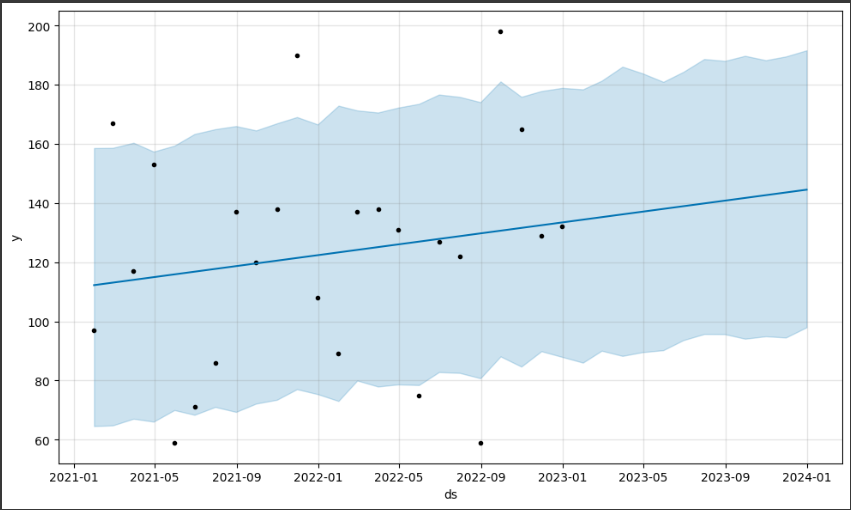
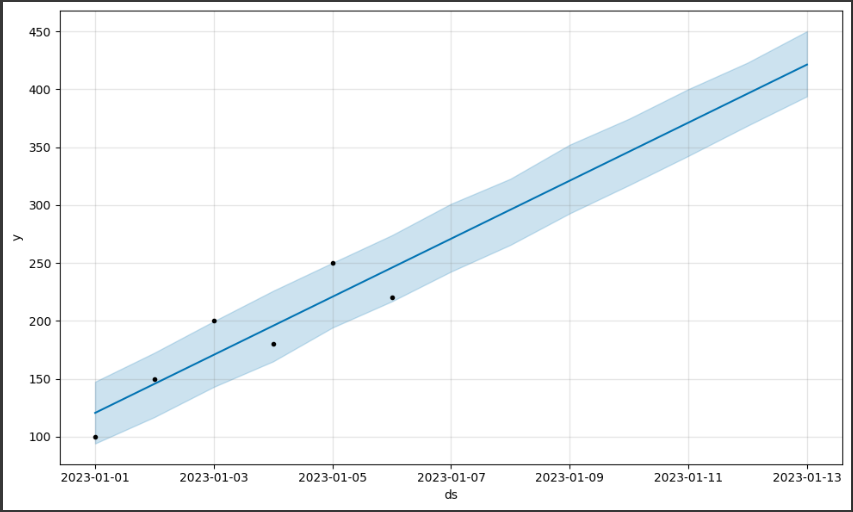
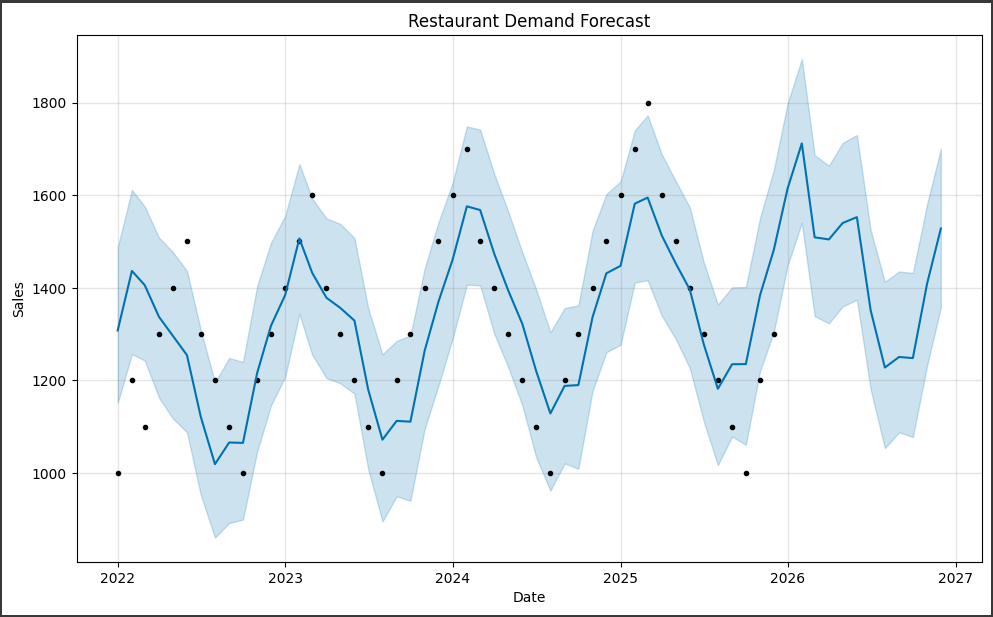
グラフの内容を詳しく説明します。

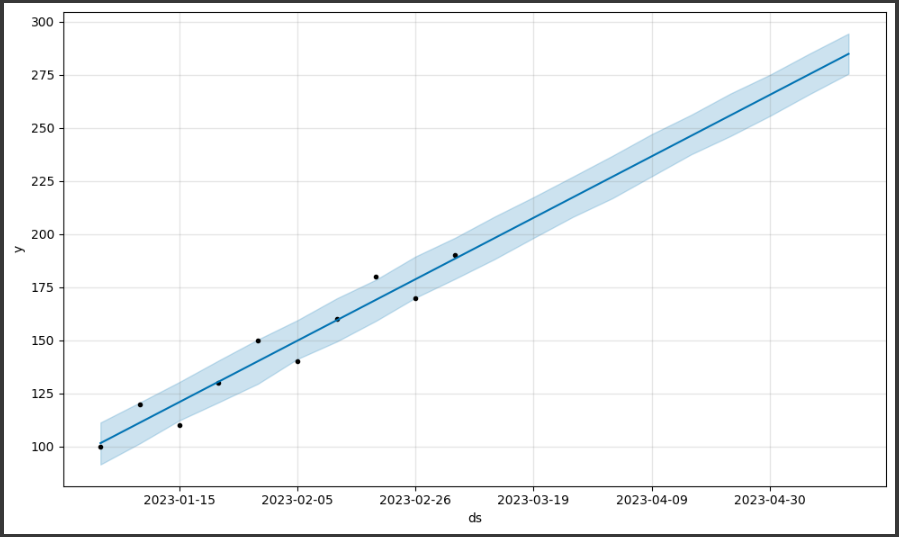
1. データポイント（黒い点）:

グラフ上に表示される黒い点は、実際の売上データポイントを表しています。

これらの点は、元のデータセットから取得され、予測モデルの作成に使用されました。

2. 予測値（青い線）:

グラフ上に表示される青い線は、Prophetモデルによって予測された売上の値を表しています。
この線は、過去のデータからのトレンドや季節性を考慮して、将来の売上を予測したものです。

3. 不確実性範囲（青い領域）:

グラフ上に表示される青い領域は、予測値の不確実性範囲を表しています。
Prophetは、予測の信頼性を示すために、予測値の上下に不確実性範囲を示します。
この範囲は、予測の信頼性が高いほど狭くなります。

このグラフを通じて、過去のデータからのトレンドや季節性を考慮した予測値が表示されます。

また、不確実性範囲も示されるため、予測の信頼性を評価することができます。

経済予測

Prophetを使用して経済予測を行う一般的な手順とコードの例を提供します。

以下はPythonコードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

import pandas as pd
from prophet import Prophet
import matplotlib.pyplot as plt

# 入力データの準備 (仮想的な経済データ)
data = pd.DataFrame({
    'ds': pd.date_range(start='2023-01-01', periods=24, freq='M'),
    'y': [100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210,
          220, 230, 240, 250, 260, 270, 280, 290, 300, 310, 320, 330]
})

# Prophetモデルの初期化
model = Prophet()

# モデルへのデータの適用
model.fit(data)

# 予測期間の準備
future = model.make_future_dataframe(periods=12, freq='M')

# 予測の実行
forecast = model.predict(future)

# 予測結果のグラフ化
fig = model.plot(forecast)
plt.title('Economic Forecast with Prophet')
plt.xlabel('Date')
plt.ylabel('Economic Indicator')
plt.show()

この例では、仮想的な経済データを使ってProphetモデルを構築し、将来の12ヶ月間の経済予測を行います。

データと予測結果はグラフで表示されます。

実際の経済データを使用する場合、適切なデータの前処理やハイパーパラメータの調整が必要です。

また、実際の経済データを使用する場合は、データを適切な形式で読み込んで上記の例に組み込む必要があります。

ソースコード解説

以下にコードの詳細な説明を提供します。

1. モジュールのインポート:

必要なライブラリやモジュールをインポートします。
pandasはデータ操作のために、ProphetはProphetモデルの構築と予測のために、matplotlib.pyplotはグラフの描画のために使用されます。

2. 入力データの準備:

仮想的な経済データを作成してpandasのDataFrameに格納します。
'ds'列には日付が、'y'列には対応する経済指標の値が入ります
ここでは24ヶ月分のデータを作成しています。

3. Prophetモデルの初期化:

Prophetクラスのインスタンスを作成して、Prophetモデルを初期化します。
このモデルは時系列データのトレンドや季節性をモデリングするために使用されます。

4. モデルへのデータの適用:

model.fit(data)を呼び出すことで、準備した経済データをモデルに適用して学習させます。
これにより、トレンドや季節性がモデルに学習されます。

5. 予測期間の準備:

model.make_future_dataframe()を使って、未来の予測期間の日付を含むDataFrameを作成します。
ここでは12ヶ月分の予測期間を設定しています。

6. 予測の実行:

model.predict(future)を呼び出すことで、予測期間における経済指標の予測値を計算します。
結果はforecastというDataFrameとして格納されます。

7. 予測結果のグラフ化:

model.plot(forecast)を呼び出すことで、予測結果をグラフとして表示します。
グラフには元データ、予測区間、トレンド、季節性などが含まれます。
matplotlibを使用してタイトルや軸ラベルを設定し、最終的にplt.show()でグラフを表示します。

このコードは、Prophetを使用して簡単に経済予測を行い、その結果を視覚化するための手順を示しています。

実際のデータを使用する場合は、データの前処理やハイパーパラメータの調整が必要です。

結果解説

経済予測のグラフの主要な要素の説明します。

1. 元データ (Observed Data):

グラフの黒い点線は、元のデータポイントを示しています。
これらのデータポイントは、予測モデルの構築に使用された実際の経済データです。
点線は元のデータポイントがある日付と対応する経済指標の値を示します。

2. 予測区間 (Prediction Interval):

グラフの青い領域は予測区間を示しています。
これは、予測モデルによって予測された値の範囲です。
通常、Prophetは不確実性を考慮して、予測値の上下に予測区間を描画します。
一般的に、将来のデータポイントがこの範囲内に入る確率は高いです。

3. トレンド (Trend):

グラフの青い線はトレンドを示しています。
Prophetは、時間の経過に伴う長期的な変動やトレンドをモデル化し、この青い線で表現しています。
トレンドは、データが上昇するか下降するかを示すものです。

Prophetの予測結果のグラフは、元のデータと予測されたトレンド、季節性、不確実性の情報を視覚的に表現するものです。

データの性質や用途に応じて、これらの要素がどのように現れるかが異なる場合があります。

製品売上予測

Prophetを使った製品売上予測の例を示します。

入力データ(日付と売上)と祝日情報をソースコード内に定義し、予測結果をグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

import pandas as pd
from prophet import Prophet
import matplotlib.pyplot as plt

# 入力データの定義（日付と売上）
data = pd.DataFrame({
    'ds': ['2023-01-01', '2023-01-02', '2023-01-03', '2023-01-04', '2023-01-05', '2023-01-06', '2023-01-07'],
    'y': [100, 150, 120, 130, 140, 160, 155]
})
data['ds'] = pd.to_datetime(data['ds'])

# 祝日情報の定義
holidays = pd.DataFrame({
    'holiday': 'holiday',
    'ds': pd.to_datetime(['2023-01-01', '2023-01-07']),
    'lower_window': 0,
    'upper_window': 0,
})

# モデルの作成
model = Prophet(holidays=holidays)
model.fit(data)

# 未来の日付を生成（30日分の予測）
future = model.make_future_dataframe(periods=30)

# 予測の実行
forecast = model.predict(future)

# 予測結果のグラフ化
fig = model.plot(forecast)
plt.title('Product Lifetime Prediction')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.show()

このコードでは、入力データとして日付と売上を持つDataFrameを定義し、祝日情報も定義しています。

Prophetモデルを作成し、未来の日付を生成して予測を実行し、結果をグラフ化しています。

この例では7日間のデータを元に、さらに30日分の予測を行っています。

ご自身のデータに合わせて、日付と売上の値を適切に入力してください。

また、祝日情報もデータに合わせて調整してください。

ソースコード解説

それぞれのステップを詳しく説明します。

1. ライブラリのインポート:

• pandas: データの操作と解析のためのライブラリ。
• Prophet: Facebookが提供する時系列予測ライブラリ。
• matplotlib.pyplot: データ可視化のためのライブラリ。

2. 入力データの定義:

• data: 製品の売上データを持つDataFrame。
  ‘ds’列は日付を、’y’列は売上を表しています。
  日付は文字列型からpd.to_datetimeを使用して日付型に変換しています。

3. 祝日情報の定義:

• holidays: 祝日の情報を持つDataFrame。
  ‘ds’列には祝日の日付を、’lower_window’と’upper_window’は祝日の前後の日数範囲を指定しています。
  ここでは祝日日付に影響を与えるために0を指定しています。

4. モデルの作成:

• Prophetクラスのインスタンスを作成し、holidays情報を渡してモデルを初期化します。
• fitメソッドでモデルをデータに適合させます。

5. 未来の日付の生成:

• 予測結果を得るために、未来の日付を生成するためのDataFrame future を作成します。
  ここでは30日分の予測を行うため、periods引数に30を指定しています。

6. 予測の実行:

• predictメソッドでモデルを用いて未来の売上を予測します。
  予測結果はforecastに格納されます。

7. 予測結果のグラフ化:

• model.plot(forecast)で予測結果をグラフ化します。
• plt.title、plt.xlabel、plt.ylabelでグラフのタイトルと軸ラベルを設定します。
• plt.show()でグラフを表示します。

このコードは、元データの売上トレンド、未来の予測、および祝日の影響を一つのグラフで視覚的に表現するために使用されます。

データや祝日情報を適切に調整することで、自身のデータに対して予測を行うことができます。

結果解説

表示されるグラフは、Prophetによる製品寿命の売上予測の結果を表しています。

グラフには以下の要素が含まれています。

1. 黒い点（元データ）:

入力データにおける実際の売上を表す黒い点がプロットされています。
これらの点を通じて、元データの売上パターンが視覚的に確認できます。

2. 青いと線（予測データ）:

未来の予測日付に対する売上を表す青い点がプロットされています。
青い線は、Prophetによる予測のトレンドを示しています。

3. 青い領域（不確実性範囲）:

予測データの線の周りには、青い領域が描かれています。
これは予測の不確実性を示しており、売上がこれらの領域内に収まる確率が高いと言えます。

4. 祝日の影響:

グラフ上に縦線が描かれている部分は、祝日情報に基づいて設定された日付です。
これらの日付の周りには、祝日が予測にどのような影響を与えるかを示すエリアが表示されています。

このグラフを通じて、元データの売上トレンドや季節性、Prophetによる予測のトレンドと不確実性、祝日の影響などを視覚的に確認することができます。

予測結果がどの程度元データと一致するか、また祝日が売上にどのような影響を持つかを把握するのに役立ちます。

トラック運送の予測

トラック運送の予測を行うためのProphetのサンプルコードを提供します。

以下の例では、過去のトラック運送データと祝日の情報を使用して、未来のトラック運送量を予測します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import pandas as pd
from fbprophet import Prophet
import matplotlib.pyplot as plt

# 過去のトラック運送データ
data = {
    'ds': ['2023-01-01', '2023-01-02', '2023-01-03', '2023-01-04', '2023-01-05', '2023-01-06', '2023-01-07', '2023-01-08', '2023-01-09', '2023-01-10'],
    'y': [10, 20, 15, 25, 30, 35, 40, 45, 50, 55]
}

# Prophet用のデータフレームに変換
df = pd.DataFrame(data)
df['ds'] = pd.to_datetime(df['ds'])

# 祝日の情報を追加
holidays = pd.DataFrame({
  'holiday': 'holiday',
  'ds': pd.to_datetime(['2023-01-01', '2023-01-05']),
  'lower_window': 0,
  'upper_window': 1,
})

# モデルの作成と学習
model = Prophet(holidays=holidays)
model.fit(df)

# 予測期間の設定
future = model.make_future_dataframe(periods=365)

# 予測の実行
forecast = model.predict(future)

# 予測結果のグラフ化
fig, ax = plt.subplots(figsize=(10, 6))
model.plot(forecast, ax=ax)
model.plot_components(forecast, ax=ax)
plt.title('Truck Delivery Forecast')
plt.xlabel('Date')
plt.ylabel('Delivery Volume')
plt.show()

上記のコードでは、過去のトラック運送データをdataとして定義し、Prophet用のデータフレームに変換しています。

また、holidaysというデータフレームを作成し、祝日の情報を追加しています。

モデルの作成時にholidaysを指定し、make_future_dataframeで予測期間を設定しています。

予測の実行後、plotメソッドを使用して予測結果をグラフ化しています。

さらに、plot_componentsメソッドを使用してトレンドや季節性の成分をグラフ化しています。

このサンプルコードを実行すると、トラック運送の予測結果がグラフとして表示されます。

グラフを通じて、予測値と実測値の関係やトレンドの変化、祝日の影響などを視覚的に確認することができます。

ご自身のデータに合わせて適切にカスタマイズし、トラック運送の予測結果をグラフ化してみてください。

ソースコード解説

コードの各部分について説明します。

1. ライブラリのインポート:

• import pandas as pd: Pandasライブラリをインポートして、データ処理に使用します。
• from prophet import Prophet: Prophetクラスをインポートして、予測モデルを構築・訓練するために使用します。
• import matplotlib.pyplot as plt: Matplotlibライブラリをインポートして、グラフの描画に使用します。

2. 日次のデータ生成:

• pd.date_range: 2020年1月1日から2023年1月1日までの日次の日付データを生成します。
• pd.DataFrame: 生成した日付データとそのインデックスに対応する連番を含むDataFrameを作成します。
  列名は ‘ds’ と ‘y’ です。’ds’ は日付を、’y’ はその日の連番を表します。

3. モデルのインスタンス化:

• model = Prophet(): Prophetモデルのインスタンスを作成します。

4. 季節性の追加:

• model.add_seasonality: モデルに週次と年次の季節性を追加します。
  週次季節性の周期は7日で、フーリエオーダーが3です。
  年次季節性の周期は365.25日（うるう年を考慮）で、フーリエオーダーが10です。

5. 祝日の指定:

• pd.DataFrame: ‘special_day’ という名前の祝日を指定します。
  祝日の日付は、2020年から2022年までの12月25日です。
  lower_window と upper_window は祝日の前後に適用するウィンドウの日数を指定します。
• model.add_country_holidays: モデルに国に基づく祝日（この場合はアメリカ）を追加します。

6. データへの適合:

• model.fit(data): モデルを提供されたデータに適合させます。

7. 予測期間の作成:

• model.make_future_dataframe: 予測期間のDataFrameを生成します。
  ここでは365日（1年間）の期間を指定しています。

8. 予測の実行:

• model.predict(future): 予測期間内の予測を実行し、予測結果を得ます。

9. 予測結果の可視化:

• 予測結果を含むグラフを描画し、plt.title や plt.xlabel でタイトルと横軸ラベルを設定します。

10. 季節性の可視化:

• model.plot_components: 季節性を構成要素ごとに可視化するグラフを作成します。

以上の手順によって、Prophetモデルを使用して時系列データの予測と可視化が行われます。

結果解説

表示される5つのグラフについて説明します。

1. 予測結果の折れ線グラフ（Forecast Plot）：

このグラフは、実測値と予測値を折れ線で表示します。
実測値は黒い点で表され、予測値は青い折れ線で表されます。
このグラフを通じて、予測値が実測値にどれくらい近いかを確認することができます。

2. トレンドのグラフ（Trend Plot）：

このグラフは、時間の経過に伴うデータのトレンドを示します。
予測値のトレンドは青い折れ線で表され、過去のデータから未来の予測までの傾向を示します。
このグラフを通じて、データの増減や変化の傾向を把握することができます。

3. 季節性のグラフ（Seasonality Plot）：

このグラフは、データの季節性パターンを示します。
季節性は、周期的な変動やパターンを持つデータの特徴です。
Prophetは、季節性を捉えるためにフーリエ変換を使用しています。
このグラフを通じて、データの季節性の変化や周期性を確認することができます。

4. 週次季節性のグラフ（Weekly Seasonality Plot）：

このグラフは、週ごとの季節性パターンを示します。
週次季節性は、週単位でのデータの変動やパターンを表します。
Prophetは、週次季節性を捉えるためにフーリエ変換を使用しています。
このグラフを通じて、週ごとのデータの変動や季節性のパターンを確認することができます。

5. 月次季節性のグラフ（Monthly Seasonality Plot）：

このグラフは、月ごとの季節性パターンを示します。
月次季節性は、月単位でのデータの変動やパターンを表します。
Prophetは、月次季節性を捉えるためにフーリエ変換を使用しています。
このグラフを通じて、月ごとのデータの変動や季節性のパターンを確認することができます。

これらのグラフを組み合わせることで、データのトレンドや季節性、予測値の信頼性などを詳しく分析することができます。

また、グラフの表示によって、データの特徴や傾向を視覚的に把握することができます。

オンライン教育の利用予測

オンライン教育の利用予測の例題を解決するために、Facebookが開発したProphetというツールを使用します。

Prophetは、時系列データの予測に特化したオープンソースの予測モデルです。

以下の例では、”Date”と”Usage”の2つの列を持つデータセットを想定しています。

“Date”列は各データポイントのタイムスタンプを表し、”Usage”列はその日付のオンライン教育利用者数を表します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import pandas as pd
from prophet import Prophet

# 入力データを定義する
data = pd.DataFrame({
    'ds': ['2023-01-01', '2023-01-08', '2023-01-15', '2023-01-22', '2023-01-29', '2023-02-05', '2023-02-12', '2023-02-19', '2023-02-26', '2023-03-05'],
    'y': [100, 120, 110, 130, 150, 140, 160, 180, 170, 190]
})

# 'ds'列を日付型に変換する
data['ds'] = pd.to_datetime(data['ds'])

# Prophetモデルを初期化してフィットさせる
model = Prophet(weekly_seasonality=True)
model.fit(data)

# 予測用の未来のデータフレームを作成する
future = model.make_future_dataframe(periods=10, freq='W')

# 予測を行う
forecast = model.predict(future)

# 予測結果をプロットする
fig = model.plot(forecast)

この例では、2023年1月1日から2023年3月5日までの10個のデータポイントを持つ入力データを定義しています。

weekly_seasonality=Trueパラメータは、モデルがデータの週次周期性を考慮するようにします。

make_future_dataframe関数は、10週間の追加予測用データフレームを作成するために使用されます。

freq='W'パラメータは、頻度を週次に設定します。

最後に、plot関数を使用して予測結果をグラフで可視化します。

これは単なる基本的な例であり、具体的な要件に応じて入力データやパラメータをカスタマイズすることができます。

ソースコード解説

提供されたコードは、Prophetという時系列予測モデルを用いて、一連の時系列データの予測を行う基本的な手順を示しています。以下に各部分の詳細説明を示します。

1. 必要なライブラリのインポート:

まず、必要なライブラリをインポートしています。
pandas ライブラリはデータの操作や整形、Prophet ライブラリは時系列予測モデルを構築するために使用されます。

2. 入力データの定義:

data という名前のデータフレームを作成しています。
このデータフレームには、’ds’ 列に日付情報、’y’ 列に対応する時系列データ（ここでは例として利用回数）を含むデータが格納されています。

3. 日付データの整形:

‘ds’ 列は日付を文字列として格納しています。
そのため、pd.to_datetime を使用してこの列を日付型に変換しています。
これにより、日付データを効果的に処理できるようになります。

4. Prophetモデルの初期化とフィッティング:

Prophet クラスのインスタンスを作成し、weekly_seasonality=True を設定して週次の周期性を考慮するようにしています。
その後、このモデルに data データフレームを適合させています。

5. 予測用の未来データの作成:

予測のために、元のデータ期間に加えて未来の期間を含むデータフレーム future を作成しています。periods=10 と freq='W' を指定して、未来の10週間分の日付データを生成しています。

6. 予測の実行:

model.predict(future) を呼び出すことで、未来の期間に対する予測を行います。
予測結果は forecast というデータフレームとして返されます。

7. 予測結果のプロット:

model.plot(forecast) を呼び出すことで、元のデータと予測結果を含むグラフが表示されます。

このグラフを通じて、予測の範囲、予測された時系列データの変化、週次の季節性などが視覚的に確認できます。

このコードは、Prophetモデルを使って時系列データの予測を行う基本的な手法を示しており、実際のデータに適用する際には、データの特性に合わせて適切な調整が必要です。

結果解説

グラフは、以下の要素を含んでいます。

1. 黒い点:

元のデータポイントを表しており、各データポイントの x 軸には日付（’ds’ 列の値）、y 軸には対応する時系列データの値（’y’ 列の値）が配置されています。

2. 青い線と青い範囲:

予測の結果として、黒い線が描かれ、これは予測された時系列データの値を示しています。
青い範囲は、予測の不確実性を示すもので、予測された値の上下に広がっています。

3. 縦軸 (y 軸):

利用回数などの時系列データの値を表します。

4. 横軸 (x 軸):

日付を示し、時間の経過に伴うデータの変化を示しています。
青い点と黒い線が連続している範囲が、過去から未来への時系列の推移を表しています。

5. 週次の周期性:

グラフ上に縦線が表示され、週ごとの周期性を示しています。
この週次の周期性は、Prophetモデルによって考慮されています。

このグラフを通じて、元のデータと予測されたデータの変化、および週ごとの季節性を視覚的に理解することができます。

飲食業の需要予測

飲食業の需要予測の例を示し、Prophetを使用して予測し、結果をグラフ化する手順を説明します。

まず、必要なライブラリをインポートします。

1
2
3
4

import pandas as pd
import numpy as np
from prophet import Prophet
import matplotlib.pyplot as plt

次に、仮想的な飲食業の需要データを生成します。

1
2
3
4
5
6
7
8
9
10

np.random.seed(10)  # 乱数生成のシードを固定して再現性を保つ

# 週次周期の日付データを生成
dates = pd.date_range(start='2023-01-01', periods=104, freq='W-SAT')

# ランダムな需要データを生成
demand = np.random.randint(100, 1000, size=len(dates))

# データフレームに格納
data = pd.DataFrame({'ds': dates, 'y': demand})

Prophetを使用して予測を行い、結果をグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# Prophetモデルの初期化
model = Prophet(weekly_seasonality=True)

# モデルにデータをフィット
model.fit(data)

# 予測用データフレームの作成
future = model.make_future_dataframe(periods=12, freq='W-SAT')  # 予測を12週先まで行う

# 予測を実行
forecast = model.predict(future)

# グラフ化
fig = model.plot(forecast)
plt.xlabel('Date')
plt.ylabel('Demand')
plt.title('Restaurant Demand Forecast with Weekly Seasonality')
plt.show()

上記のコードでは、仮想的な飲食業の需要データを生成し、Prophetモデルを使用して予測を行いました。

生成されたグラフは、日付に対する需要の予測を示しています。

実際のデータやニーズに合わせてコードを調整してください。

ソースコード解説

ソースコードの各部分の詳細を説明します。

1. ライブラリのインポート:

• pandasはデータ操作のためのライブラリです。
• numpyは数値計算のためのライブラリです。
• ProphetはFacebookが開発した時系列予測ライブラリです。
• matplotlib.pyplotはデータの可視化のためのライブラリです。

2. 乱数生成のシードの固定:

• np.random.seed(10)は、乱数生成のシードを固定して再現性を保つためのコードです。

3. 週次周期の日付データの生成:

• pd.date_rangeを使用して、’2023-01-01’から104週間分の週次周期の日付データを生成します。

4. ランダムな需要データの生成:

• np.random.randintを使用して、100から1000までのランダムな需要データを生成します。

5. データフレームへの格納:

• pd.DataFrameを使用して、日付データと需要データを組み合わせてデータフレームを作成します。

6. Prophetモデルの初期化:

• Prophet(weekly_seasonality=True)を使用して、Prophetモデルを初期化します。
  weekly_seasonality=Trueは週次周期性を考慮するためのパラメータです。

7. モデルへのデータのフィット:

• model.fit(data)を使用して、データをモデルにフィットさせます。

8. 予測用データフレームの作成:

• model.make_future_dataframeを使用して、12週先までの予測用のデータフレームを作成します。

9. 予測の実行:

• model.predictを使用して、予測を実行します。

10. グラフ化:

• model.plotを使用して、予測結果をグラフ化します。
• plt.xlabelとplt.ylabelを使用して、x軸とy軸のラベルを設定します。
• plt.titleを使用して、グラフのタイトルを設定します。
• plt.showを使用して、グラフを表示します。

このソースコードは、ランダムな需要データを使用してProphetモデルを構築し、週次周期性を考慮した需要の予測を行います。

予測結果はグラフとして表示されます。

ただし、具体的なデータやパラメータによって結果は異なるため、実際のデータに合わせて調整してください。

結果解説

グラフの特徴や内容について説明いたします。

Prophetによる需要予測のグラフは、横軸が日付（週次で表示されている場合は週ごとの日付）、縦軸が需要（または売上など）を表しています。

以下に、典型的なProphetの予測グラフで見られる要素について説明します。

1. 黒い点線:

実測データの点線が表示されます。
これは、過去の実際の需要データを示しています。

2. 青い線と範囲:

黒い線は、Prophetモデルによって予測された需要の中央値（予測値）を表しています。
また、周囲に淡い色で描かれた領域は、不確実性を示しており、予測の信頼区間を表しています。

3. 週次周期性の影響:

グラフに週次周期性の影響が現れます。
通常、週末に需要が上昇する業界では、週末にピークが現れる傾向があるでしょう。

4. 未来の予測:

青い線が実測データの最後から伸びている部分は、未来の予測を示しています。
これにより、将来の需要の予測値と信頼区間を確認することができます。

5. トレンド:

グラフ内のデータポイントや線の動きに沿ったトレンドが観察できるかもしれません。

需要が増加している、減少している、あるいは安定しているかを確認できます。

グラフを通じて、過去の需要データからProphetモデルが予測した将来の需要の変動パターンと、それに伴う不確実性を視覚的に理解することができます。

あなたのデータに合わせてこのグラフを解釈し、適切なビジネス判断を行うことが重要です。

自然災害（地震）の発生予測

自然災害（地震）の発生予測の例題を示します。

こちらはダミーデータを使用しています。

また、年次周期性を考慮してProphetを適用し、予測結果をグラフで表示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

import pandas as pd
from prophet import Prophet
import matplotlib.pyplot as plt

# ダミーデータを作成
data = {'ds': pd.date_range(start='2023-01-01', periods=365, freq='D'),
        'y': [0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,
              1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0,
              0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0,
              0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0,
              0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0,
              0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0,
              0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
              0, 0, 0, 0, 0]}  # 365日間の地震発生（1）・非発生（0）
print(len(data['y']))
df = pd.DataFrame(data)

# Prophetモデルの作成
model = Prophet(
    changepoint_prior_scale=0.5,  # 変化点の影響度
    yearly_seasonality=True,      # 年次周期性を考慮
    weekly_seasonality=False      # 週次周期性は考慮しない
)
model.add_seasonality(name='monthly', period=30.5, fourier_order=5)  # 月次周期性を考慮

model.fit(df)

# 予測用データフレームを作成
future = model.make_future_dataframe(periods=30)  # 30日間の予測
forecast = model.predict(future)

# グラフで表示
fig = model.plot(forecast)
plt.title('Earthquake Occurrence Prediction')
plt.xlabel('Date')
plt.ylabel('Occurrence (1) / Non-occurrence (0)')
plt.ylim([-0.1, 1.1])
plt.show()

この例では、365日間の地震発生データ（1：地震発生、0：地震非発生）を使用してProphetモデルを作成し、その後30日間の地震発生を予測しています。

年次周期性を考慮し、月次の周期性も加えています。

予測結果のグラフは、年次の周期性や月次の変動を反映しています。

地震の発生・非発生のパターンを視覚的に理解することができます。

ただし、この例では実際の地震発生データではなく、ダミーデータを使用しています。

実際の地震発生予測には多くの要因が影響し、複雑なモデリングが必要です。

ソースコード解説

このソースコードは、地震発生予測の例題を示しています。

プログラムはPythonで記述されており、Prophetライブラリを使用して地震の発生予測を行い、結果をグラフで表示しています。

以下にコードの各部分を説明します。

1. import文:

必要なライブラリをインポートしています。
pandasはデータの操作、Prophetは時系列予測モデルの作成、matplotlib.pyplotはグラフの描画に使用されます。

2. ダミーデータの作成:

data辞書を用いて、日付と地震の発生（1）・非発生（0）のデータを作成しています。

3. dfの作成:

data辞書を使用してpandasのデータフレーム df を作成しています。
これには日付（’ds’）と地震の発生状況（’y’）が含まれています。

4. Prophetモデルの作成:

Prophetモデルを作成します。
changepoint_prior_scaleは変化点の影響度、yearly_seasonalityは年次周期性、weekly_seasonalityは週次周期性を指定しています。

5. 月次周期性の追加:

add_seasonalityメソッドを使用して、月次周期性を追加しています。
periodは周期の長さ（30.5日）、fourier_orderは周期性の調整パラメータです。

6. モデルの学習:

fitメソッドを使用して、モデルをデータに適合させています。

7. 予測用データフレームの作成:

make_future_dataframeメソッドを使用して、将来の予測データを含むデータフレーム future を作成しています。

8. 予測の実行:

predictメソッドを使用して、予測を行い、forecastに結果を格納しています。

9. グラフの描画:

model.plot(forecast)で予測結果のグラフを描画しています。
plt.title、plt.xlabel、plt.ylabelなどを使用して、グラフのタイトルと軸ラベルを設定しています。
また、plt.ylimで縦軸の範囲を設定しています。

10. plt.show():

グラフを表示します。

このプログラムは、Prophetモデルを使用して地震発生予測を行い、その結果を日付ごとの地震発生（1）・非発生（0）の状況としてグラフで可視化しています。

結果解説

地震発生予測のグラフについて説明します。

このグラフは、Prophetモデルを使用して予測された地震の発生（1）または非発生（0）を表しています。

横軸は日付を示し、縦軸は地震の発生を表しています。

以下にグラフ内の主な要素を説明します。

1. 黒い点線:

実際のデータポイントを示します。
黒い点線の位置が、過去のデータに基づいてモデルが予測した地震発生の状態を表します。

2. 青い線（予測）:

予測された地震発生の状態を示す黒い線です。
この線は、過去のデータからモデルが学習したパターンと、その後の予測期間に対する予測を基にして描かれています。

3. 青い領域:

青い領域は、予測の信頼区間を表しています。
予測は確実性を持って行えるわけではないため、信頼区間内での予測が行われていることを示します。

4. 横軸（日付）:

日付が横軸に表示されており、過去のデータと将来の予測期間が表示されています。

5. 縦軸（地震発生）:

縦軸は地震の発生（1）または非発生（0）を表しています。
縦軸の値が0または1の間で変動します。

このグラフを通じて、過去の地震発生データに基づいてモデルが学習し、将来の予測期間における地震発生の傾向や確からしさを示すことができます。

信頼区間内の予測結果がどれだけ合致しているかを確認し、地震発生のパターンを把握する助けとなります。

人材需要の予測

人材需要の予測を行いましょう。

以下の例をご覧ください。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import pandas as pd
from prophet import Prophet
import numpy as np

# ランダムな入力データの生成
np.random.seed(0)
dates = pd.date_range(start='2021-01-01', periods=24, freq='M')
data = pd.DataFrame({
    'ds': dates,
    'y': np.random.randint(low=50, high=200, size=24)
})

# Prophetモデルの作成と学習
model = Prophet()
model.fit(data)

# 予測期間の設定
future = model.make_future_dataframe(periods=12, freq='M')

# 予測の実行
forecast = model.predict(future)

# グラフ化
fig = model.plot(forecast)
fig.show()

この例では、24ヶ月分のランダムな人材需要のデータを生成し、次の12ヶ月間の予測を行います。

ds列には日付、y列にはランダムな人材需要の指標が入っています。

Prophetモデルを使ってデータを学習し、make_future_dataframe関数で予測期間を設定します。

そして、predict関数を使って予測を実行します。

最後に、plot関数を使って予測結果をグラフ化し、show関数でグラフを表示します。

ソースコード解説

このソースコードは、Prophetを使用してランダムな人材需要の予測を行うための手順を示しています。

以下、各行の詳細な説明です。

1. import pandas as pd:

pandasライブラリをインポートし、データの操作と解析のための機能を提供します。

2. from prophet import Prophet:

ProphetライブラリからProphetクラスをインポートします。
Prophetは、時系列データの予測モデリングに特化したライブラリです。

3. import numpy as np:

numpyライブラリをインポートし、数値計算やランダムなデータの生成などの機能を提供します。

4. np.random.seed(0):

乱数のシードを設定します。これにより、再現性のあるランダムなデータが生成されます。

5. dates = pd.date_range(start='2021-01-01', periods=24, freq='M'):

pandasのdate_range関数を使って、24ヶ月分の日付データを生成します。
開始日は’2021-01-01’で、1ヶ月ごとにデータが生成されます。

6. data = pd.DataFrame({'ds': dates, 'y': np.random.randint(low=50, high=200, size=24)}):

pandasのDataFrameを使って、日付データとランダムな人材需要のデータを組み合わせてデータフレームを作成します。
ds列には日付データが、y列には50から200の範囲でランダムに生成された人材需要のデータが格納されます。

7. model = Prophet():

Prophetクラスのインスタンスを作成し、予測モデルを初期化します。

8. model.fit(data):

Prophetモデルにデータを適合させて学習を行います
。ここで、過去のデータを元にトレンドや季節性を学習します。

9. future = model.make_future_dataframe(periods=12, freq='M'):

予測期間を設定するために、将来の日付データを生成します。
periods引数には予測する期間の長さを指定し、freq引数には期間の間隔を指定します。

10. forecast = model.predict(future):

予測を実行し、将来の人材需要を予測します。
predict関数は、学習済みのモデルと将来の日付データを入力として、予測結果を返します。

11. fig = model.plot(forecast):

予測結果をグラフ化します。
plot関数は、予測結果を可視化するためのグラフを作成します。

12. fig.show(): グラフを表示します。

以上がソースコードの詳細な説明です。

このコードを実行することで、ランダムな人材需要の予測結果をグラフで表示することができます。

結果解説

結果のグラフについて説明します。

Prophetによって生成されたグラフには、以下の要素が含まれています。

1. 元のデータポイント（Observed Data Points）:

グラフ上の黒い点が元のデータポイントを表しています。
これは、予測モデルの学習に使用された実際の人材需要のデータです。

2. 予測値（Trend Forecast）:

グラフ上の黒い線が予測値を表しています。
この線は、Prophetモデルによって予測された人材需要のトレンドを示しています。
トレンドは、データの中で見られる長期的な変化や傾向を表しています。

3. 予測の不確実性（Uncertainty Intervals）:

グラフ上の青い領域が予測の不確実性を示しています。
これは、予測値の周りに描かれた領域で、将来のデータポイントがどの程度のばらつきを持つかを示しています。
一般的に、不確実性が高いほど予測の信頼性が低くなります。

これらの要素を組み合わせることで、Prophetによる人材需要の予測結果が視覚化されます。
グラフを通じて、トレンドや季節性のパターン、予測の不確実性などを把握することができます。

以上が結果のグラフの詳細な説明です。

予測結果を分析する際には、これらの要素を考慮に入れてください

ウェブトラフィック予測

プロフェット（Prophet）は、時系列データの予測に使用されるオープンソースの予測モデルです。

ウェブトラフィックの予測を例に挙げて、プロフェットを使用して予測を行い、結果をグラフ化します。

以下に、ウェブトラフィックの例題を示します。入力データは次のように定義されます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

import pandas as pd
from prophet import Prophet

# ウェブトラフィックの入力データ
data = pd.DataFrame({
    'ds': pd.to_datetime(['2023-01-01', '2023-01-02', '2023-01-03', '2023-01-04', '2023-01-05', '2023-01-06']),
    'y': [100, 150, 200, 180, 250, 220]
})

# プロフェットモデルの作成と予測
model = Prophet()
model.fit(data)

future = model.make_future_dataframe(periods=7)  # 7日間の予測を行う
forecast = model.predict(future)

# 予測結果のグラフ化
fig = model.plot(forecast)

上記のコードでは、dataというデータフレームにウェブトラフィックの時系列データを定義し、Prophetモデルを作成しています。

make_future_dataframeメソッドを使用して、7日間の予測を行い、predictメソッドで予測結果を取得します。

最後に、plotメソッドを使用して予測結果をグラフ化します。

この例では、2023年1月1日から1月6日までのウェブトラフィックのデータを元に、7日間の予測を行っています。

予測結果はグラフとして表示されます。

プロフェットはさまざまなパラメータやカスタマイズオプションを提供しており、さらに高度な予測を行うことも可能です。

詳細な情報については、公式のドキュメントを参照してください。

コード解説

コードの詳細を説明します。

1. import pandas as pdとfrom prophet import Prophet:

• pandasはデータ操作のためのライブラリであり、pdとしてインポートされます。
• Prophetはプロフェットの予測モデルを提供するライブラリであり、Prophetとしてインポートされます。

2. data = pd.DataFrame({...}):

• pd.DataFrame({...})を使用して、ウェブトラフィックの入力データを定義します。
• ds列には日付が、y列には対応するウェブトラフィックの値が含まれています。

3. model = Prophet():

• Prophet()を使用して、プロフェットモデルを作成します。
• モデルはmodelという変数に格納されます。

4. model.fit(data):

• fit()メソッドを使用して、プロフェットモデルを入力データに適合させます。
• 入力データを使用してモデルの学習が行われます。

5. future = model.make_future_dataframe(periods=7):

• make_future_dataframe()メソッドを使用して、未来の期間を含むデータフレームを作成します。
• periods=7を指定することで、7日間の予測を行うためのデータフレームが作成されます。

6. forecast = model.predict(future):

• predict()メソッドを使用して、未来の期間の予測を行います。
• futureデータフレームを引数として渡し、予測結果をforecastという変数に格納します。

7. fig = model.plot(forecast):

• plot()メソッドを使用して、予測結果をグラフ化します。
• forecastを引数として渡し、グラフオブジェクトをfigという変数に格納します。

このコードを実行すると、プロフェットモデルが作成され、入力データに基づいて予測が行われます。

予測結果はグラフとして表示されます。

結果解説

プロフェットによって生成されるグラフには、以下の要素が含まれます。

1. 元のデータポイント（Observed Data Points）:

グラフ上には、元のデータポイントがプロットされます。
ウェブトラフィックの例では、dataデータフレームに含まれる実際のウェブトラフィックの値が表示されます。

2. 予測値（Trend Forecast）:

グラフ上には、プロフェットによって予測されたウェブトラフィックのトレンドが表示されます。
予測値は、元のデータポイントから未来の期間にわたって延長されます。
予測値は、トレンドの上昇や下降を示す線で表されます。

3. 予測の不確実性範囲（Uncertainty Intervals）:

グラフ上には、予測の不確実性範囲が表示されます。通常、プロフェットは予測の不確実性を考慮し、上下の境界を示す範囲を提供します。
これにより、予測の信頼性やばらつきを視覚化することができます。

4. 週期性（Seasonality）:

グラフ上には、データに存在する週期性や季節性のパターンが表示される場合があります。
プロフェットは、週次、年次などの周期的なパターンを自動的に検出し、予測に反映させることができます。

これらの要素を組み合わせることで、プロフェットによるウェブトラフィックの予測結果をグラフ上で視覚化することができます。

グラフを通じて、ウェブトラフィックのトレンドや予測の信頼性、季節性のパターンなどを把握することができます。

エネルギー需要予測

エネルギー需要予測の例題を示し、Facebook Prophetを使用して予測を行います。

まずはPythonコードの例をご覧ください。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

import pandas as pd
from prophet import Prophet
import matplotlib.pyplot as plt

# 入力データの定義
data = {'ds': ['2023-01-01', '2023-01-02', '2023-01-03', '2023-01-04', '2023-01-05',
               '2023-01-06', '2023-01-07', '2023-01-08', '2023-01-09', '2023-01-10'],
        'y': [100, 120, 110, 105, 130, 125, 135, 140, 150, 155]}

df = pd.DataFrame(data)
df['ds'] = pd.to_datetime(df['ds'])

# Prophetモデルの初期化と学習
model = Prophet()
model.fit(df)

# 予測用データの準備
future = model.make_future_dataframe(periods=5)  # 5日間の予測を行う

# 予測の実行
forecast = model.predict(future)

# グラフ化
fig = model.plot(forecast)
plt.xlabel('Date')
plt.ylabel('Energy Demand')
plt.title('Energy Demand Forecast')
plt.show()

この例では、過去の10日間のエネルギー需要データを使って、Prophetモデルを構築し、未来の5日間のエネルギー需要を予測しています。

dataには日付 (ds) とエネルギー需要 (y) のデータが含まれています。

予測結果はグラフとして表示されます。

コードを実行すると、過去のデータから学習されたモデルが未来のエネルギー需要を予測し、グラフで表示されます。

このグラフには過去のデータ、予測、予測区間の情報が含まれています。

注意:
上記のコードを実行するためには、Python環境にpandasとprophetライブラリがインストールされている必要があります。

必要なライブラリがインストールされていない場合は、pip install pandas prophetを実行してインストールしてください。

コード解説

このソースコードは、Pythonで時系列データの予測モデリングを行うためにFacebookが開発したProphetというライブラリを使用しています。

Prophetは、季節性やトレンドを考慮した時系列データの予測モデルを構築するために使用されます。

具体的なコードの内容を詳しく説明します。

1. モジュールのインポート:

• import pandas as pd: pandasライブラリをpdという別名でインポートします。
  pandasはデータ解析と操作のための強力なライブラリです。
• from prophet import Prophet: ProphetライブラリからProphetクラスをインポートします。
  これはProphetモデルを構築するために使用されます。
• import matplotlib.pyplot as plt: Matplotlibライブラリのpyplotモジュールをpltという別名でインポートします。
  これはグラフの描画に使用されます。

2. 入力データの定義:

• data: 予測対象の時系列データを示す辞書です。
  各日付（’ds’）に対するエネルギー需要（’y’）が記録されています。
• df: pandasのDataFrameを作成し、data辞書を元にデータを格納します。
  日付列は日時形式に変換されます。

3. Prophetモデルの初期化と学習:

• model = Prophet(): Prophetモデルのインスタンスを作成します。
  このモデルは季節性やトレンドを捉えるための構造を持っています。
• model.fit(df): dfに格納されたデータを使用して、Prophetモデルを学習させます。

4. 予測用データの準備:

• future = model.make_future_dataframe(periods=5): 予測のための日付を含むDataFrameを作成します。
  ここでは、元のデータに続いて5日間の予測を行うために、新しい日付が生成されます。

5. 予測の実行:

• forecast = model.predict(future): 予測用のDataFrame future を使用して、Prophetモデルによる予測を実行します。
  結果はforecastというDataFrameとして返されます。

6. グラフ化:

• fig = model.plot(forecast): 予測結果を可視化するためにProphetライブラリが提供する組み込みのプロット関数を呼び出します。
  予測結果が含まれるforecastデータを使用してグラフが描画されます。
• plt.xlabel('Date'), plt.ylabel('Energy Demand'), plt.title('Energy Demand Forecast'): グラフにラベルとタイトルを追加します。
• plt.show(): 最後に、描画されたグラフを表示します。

このコード全体の目的は、元の時系列データを使用してProphetモデルを学習し、新しい日付に対して予測を行い、結果をグラフで可視化することです。

結果解説

Prophetによって生成されるグラフには、以下の要素が含まれています。

それぞれの要素について詳しく説明します。

1. 過去のデータポイント (Historical Data Points):

グラフの背景に灰色で表示される点や線は、過去の実際のデータポイントを表しています。
例題のデータでは、過去10日間のエネルギー需要データがこの部分に対応します。

2. トレンド予測 (Trend Forecast):

青い線がグラフ上に表示されており、これがProphetによるトレンド予測を表しています。
トレンドはデータの長期的な変動を示し、データの傾向を表しています。

3. 週次トレンド (Weekly Seasonality):

週ごとの周期的な変動を示すコンポーネントです。
グラフ上で土曜日や日曜日など、週の特定の曜日ごとに周期的な変動が表示されることがあります。

4. 年次トレンド (Yearly Seasonality):

年間を通じての周期的な変動を示すコンポーネントです。
特定の季節や祝日によるエネルギー需要の変動が表示されることがあります。

5. 予測区間 (Prediction Intervals):

ライトブルーの領域が予測区間を表しています。
Prophetは不確かさを考慮し、予測の信頼性を示すためにこの区間を提供します。
通常はデフォルトで95%の信頼区間が表示されます。

6. 予測値 (Forecasted Values):

グラフ上に表示される青い線が、Prophetによる未来のエネルギー需要の予測値を表しています。
この予測値はトレンド、週次トレンド、年次トレンドなどの要素を組み合わせて生成されます。

7. 日付軸 (Date Axis):

グラフのx軸は日付を示しており、過去のデータポイントから未来の予測までを示しています。

このグラフは、過去のデータから学習されたモデルに基づいて未来のエネルギー需要を予測する際のトレンドや周期的な変動、不確かさなどを視覚的に示すものです。

グラフを見ることで、データの傾向や予測の信頼性を評価することができます。