Optimizing Supply Chain Networks with NetworkX
Here’s a advanced NetworkX example that focuses on a different real-world problem: Network Flow Optimization.
In this example, we’ll use NetworkX to model a supply chain network and optimize the flow of goods from suppliers to consumers.
Problem Description:
You have multiple suppliers and consumers connected by a network of routes with limited capacity.
The goal is to find the maximum flow of goods from suppliers to consumers while respecting the capacity constraints of each route.
Python Code:
1 | import networkx as nx |
Explanation:
Graph Construction:
- Nodes represent suppliers, distribution centers (DCs), and consumers.
- Edges represent transportation routes between these entities, with capacities indicating the maximum amount of goods that can be transported along each route.
Super Source and Super Sink:
- To handle multiple sources and sinks, a super source and super sink are added to the graph. These are connected to the actual suppliers and consumers with infinite capacity edges.
Maximum Flow Calculation:
- The
nx.maximum_flowfunction calculates the maximum flow from the super source to the super sink, optimizing the distribution of goods while respecting capacity constraints.
- The
Visualization:
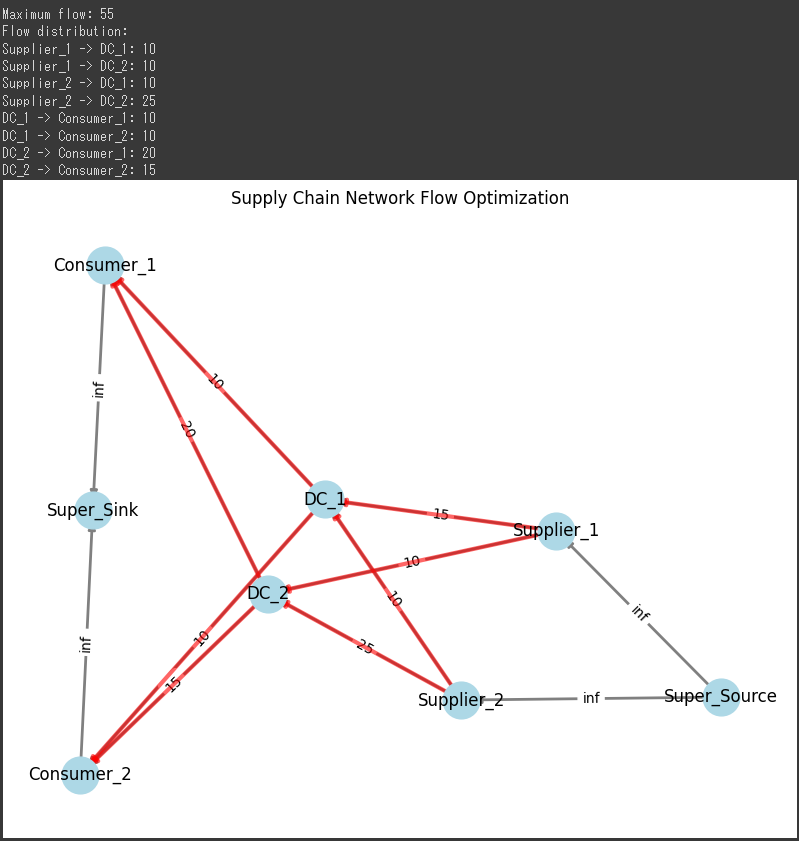
- The network is visualized with nodes and edges, and the actual flow of goods (as calculated by the algorithm) is highlighted in red.
Output:
Use Case:
This model can be used to optimize supply chain operations, such as distributing products from factories to warehouses and then to retail outlets, ensuring that capacity constraints are respected.
This example showcases NetworkX’s ability to handle complex optimization problems with network flow analysis, a critical task in operations research and logistics.