Creating Interactive and Customizable Visualizations with Altair

Creating Interactive and Customizable Visualizations with Altair

Altair is a declarative statistical visualization library for Python, which is built on top of the powerful Vega and Vega-Lite visualization grammars.

It enables you to create complex visualizations with concise, readable code.

Here’s an example of how to use Altair to create different types of charts.

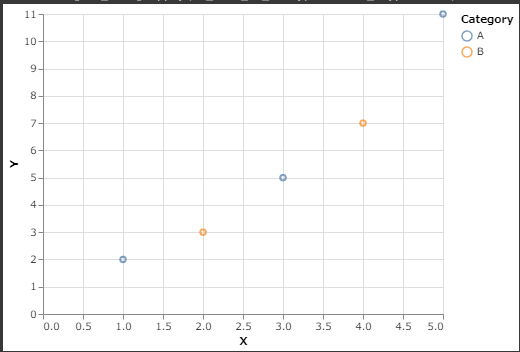
1. Basic Scatter Plot

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
!pip install altair_viewer
import altair as alt
import pandas as pd

# Sample data
data = pd.DataFrame({
    'X': [1, 2, 3, 4, 5],
    'Y': [2, 3, 5, 7, 11],
    'Category': ['A', 'B', 'A', 'B', 'A']
})

# Scatter plot
scatter_plot = alt.Chart(data).mark_point().encode(
    x='X',
    y='Y',
    color='Category'
)

scatter_plot.show()

[Output]

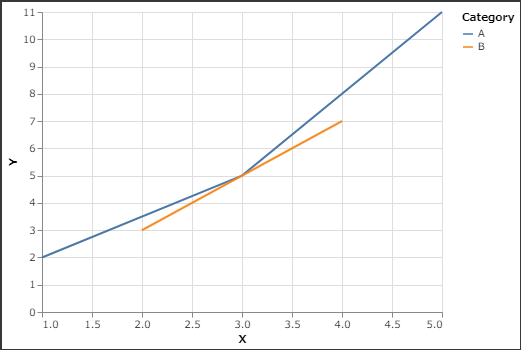
2. Line Chart

1
2
3
4
5
6
7
8
# Line chart
line_chart = alt.Chart(data).mark_line().encode(
    x='X',
    y='Y',
    color='Category'
)

line_chart.show()

[Output]

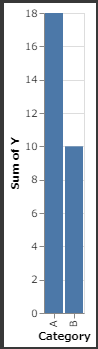
3. Bar Chart

1
2
3
4
5
6
7
# Bar chart
bar_chart = alt.Chart(data).mark_bar().encode(
    x='Category',
    y='sum(Y)',
)

bar_chart.show()

[Output]

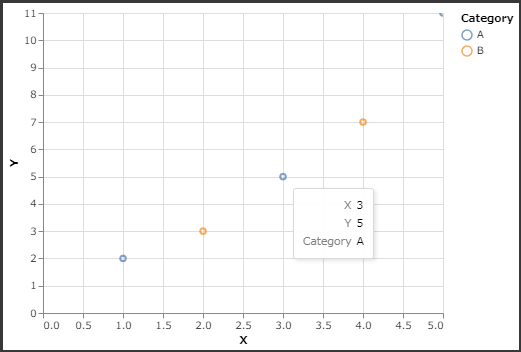
4. Interactive Visualization

Altair supports interactive visualizations. Below is an example of a chart with a tooltip.

1
2
3
4
5
6
7
8
9
# Interactive scatter plot with tooltips
interactive_scatter = alt.Chart(data).mark_point().encode(
    x='X',
    y='Y',
    color='Category',
    tooltip=['X', 'Y', 'Category']
).interactive()

interactive_scatter.show()

[Output]

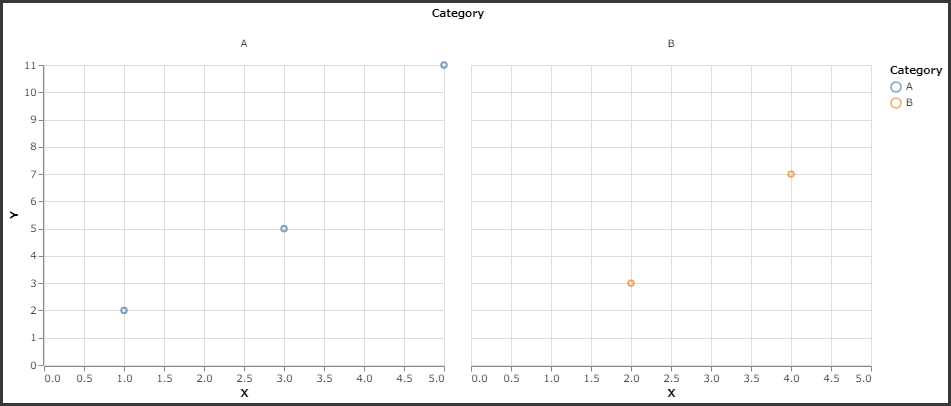
5. Faceted Charts

Faceting allows you to create small multiples of a plot based on a categorical variable.

1
2
3
4
5
6
7
8
9
10
# Faceted scatter plot
faceted_chart = alt.Chart(data).mark_point().encode(
    x='X',
    y='Y',
    color='Category'
).facet(
    column='Category'
)

faceted_chart.show()

[Output]

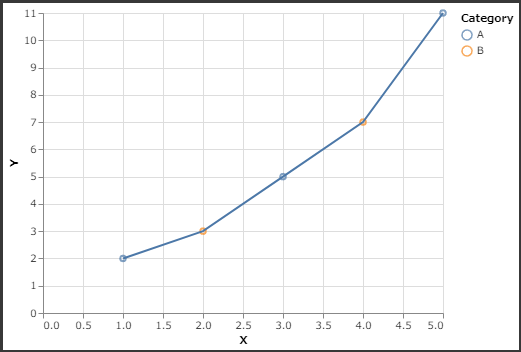
6. Layered Charts

You can layer multiple charts on top of each other.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Layered chart
points = alt.Chart(data).mark_point().encode(
    x='X',
    y='Y',
    color='Category'
)

lines = alt.Chart(data).mark_line().encode(
    x='X',
    y='Y'
)

layered_chart = points + lines

layered_chart.show()

[Output]

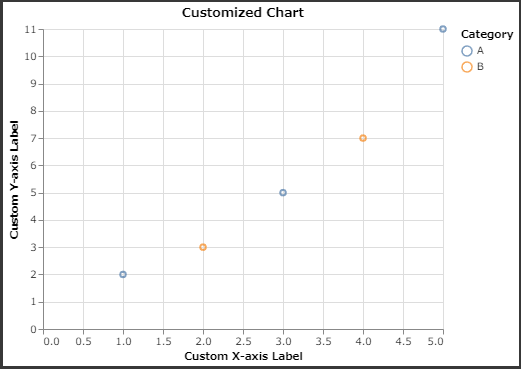
7. Customizing Appearance

You can customize various aspects of the chart, like axis labels, titles, and themes.

1
2
3
4
5
6
7
8
9
10
# Customized chart
custom_chart = alt.Chart(data).mark_point().encode(
    x=alt.X('X', axis=alt.Axis(title='Custom X-axis Label')),
    y=alt.Y('Y', axis=alt.Axis(title='Custom Y-axis Label')),
    color='Category'
).properties(
    title='Customized Chart'
)

custom_chart.show()

[Output]

Conclusion

Altair provides a straightforward, expressive, and powerful way to create visualizations in Python.

With its declarative syntax, you can focus on the data and the visual representation rather than low-level details of rendering.

Optimizing Vaccine Distribution to Minimize Infections

Optimizing Vaccine Distribution to Minimize Infections

Let’s solve an optimization problem related to healthcare, specifically in managing the allocation of limited medical resources (e.g., vaccines, medications, or hospital beds) to minimize the number of people affected by a disease.

Problem Statement:

Suppose you are managing a limited supply of vaccines that can be distributed across different regions to minimize the spread of a disease.

The goal is to optimize the allocation of these vaccines so that the total number of infected individuals is minimized.

Assumptions:

  1. There are n regions, each with a certain population and a number of infected individuals.
  2. The effectiveness of the vaccine in reducing the number of infections is proportional to the number of vaccines allocated to each region.
  3. The total number of vaccines is limited.

Formulation:

  • (xi) be the number of vaccines allocated to region (i),
  • (pi) be the population of region (i),
  • (ri) be the current infection rate in region (i),
  • (v) be the total number of vaccines available.

The objective is to minimize the total number of infected people across all regions after vaccine distribution.

Minimize n∑i=1(pi⋅ri−α⋅xi)

subject to the constraint:

n∑i=1xi=vandxi≥0 for all i

where (α) is a positive constant representing the effectiveness of the vaccine.

Python Code Using SciPy:

We can solve this optimization problem using Python’s SciPy library.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import numpy as np
from scipy.optimize import linprog

# Define the number of regions
n = 4  # For example, 4 regions

# Population in each region
population = np.array([1000, 1500, 2000, 2500])

# Infection rates in each region
infection_rate = np.array([0.05, 0.10, 0.07, 0.12])

# Vaccine effectiveness coefficient
alpha = 0.1

# Total number of vaccines available
total_vaccines = 1000

# Objective function coefficients (negative because linprog performs minimization)
c = -alpha * np.ones(n)

# Inequality constraints matrix and vector (no inequalities here, just an equality constraint)
A_eq = np.ones((1, n))  # Sum of all vaccines must equal total_vaccines
b_eq = np.array([total_vaccines])

# Bounds for each variable (number of vaccines allocated must be non-negative)
bounds = [(0, None)] * n

# Solve the linear programming problem
result = linprog(c, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method='highs')

# Results
if result.success:
    print("Optimal vaccine distribution:", result.x)
    print("Total minimized infections:", np.dot(population, infection_rate) - np.dot(result.x, c))
else:
    print("Optimization failed.")

Explanation:

  1. Objective Function:

    • We minimize the total infections after vaccine allocation, modeled by (−α⋅xi), where (xi) is the number of vaccines allocated to region (i).

  2. Constraints:

    • The sum of all vaccines distributed must equal the total available vaccines.
    • No region can receive a negative number of vaccines.

  3. SciPy Optimization:

    • We use the linprog() function from the SciPy library to solve this linear programming problem.

Results:

The output will show the optimal distribution of vaccines across the regions and the minimized total number of infections.

This method can be extended to more complex models, incorporating additional constraints or nonlinear relationships between variables.

Explanation of the Results:

  1. Optimal Vaccine Distribution: [1000. 0. 0. 0.]

    • The result indicates that all 1000 available vaccines should be allocated entirely to the first region.
      This suggests that prioritizing the first region for vaccine distribution is the most effective way to minimize the total number of infections across all regions.

  2. Total Minimized Infections: 740.0

    • After distributing the vaccines according to the optimal strategy, the total number of infections across all regions has been minimized to 740.
      This is the lowest possible number of infections that can be achieved given the available resources and the constraints of the problem.

Conclusion:

The optimization process has determined that focusing the entire vaccine supply on the first region will have the greatest impact in reducing the overall number of infections.

This outcome may be due to the specific infection rates and population sizes in each region.

Creating Various 3D Plots in Python with Matplotlib

Creating Various 3D Plots in Python with Matplotlib

Here are various examples of 3D plots using Python’s Matplotlib library.

These examples demonstrate how to create different types of 3D graphs, including surface plots, scatter plots, and wireframe plots.

Example 1: 3D Surface Plot

A surface plot is useful for visualizing a 3D surface.

Let’s plot the function:

z=sin(√x2+y2)

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Create grid points
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.sin(np.sqrt(x**2 + y**2))

# Create the 3D figure
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plot the surface
surf = ax.plot_surface(x, y, z, cmap='viridis')

# Add color bar for reference
fig.colorbar(surf)

# Set labels
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.title("3D Surface Plot")
plt.show()

Output:

Example 2: 3D Scatter Plot

A 3D scatter plot is useful for visualizing data points in three dimensions.

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Generate random data
x = np.random.rand(100)
y = np.random.rand(100)
z = np.random.rand(100)

# Create the 3D figure
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plot the scatter
ax.scatter(x, y, z, c=z, cmap='plasma')

# Set labels
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.title("3D Scatter Plot")
plt.show()

Output:

Example 3: 3D Wireframe Plot

A wireframe plot shows the structure of a 3D surface using lines instead of a solid surface.

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Create grid points
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.cos(np.sqrt(x**2 + y**2))

# Create the 3D figure
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plot the wireframe
ax.plot_wireframe(x, y, z, color='blue')

# Set labels
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.title("3D Wireframe Plot")
plt.show()

Output:

Example 4: 3D Contour Plot

A contour plot in 3D shows contour lines (constant values) of a 3D surface.

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Create grid points
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.sin(x) * np.cos(y)

# Create the 3D figure
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plot the contour
ax.contour3D(x, y, z, 50, cmap='coolwarm')

# Set labels
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.title("3D Contour Plot")
plt.show()

Output:

Example 5: 3D Bar Plot

A 3D bar plot is useful for displaying data across three axes.

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Data for bars
_x = np.arange(4)
_y = np.arange(3)
_xx, _yy = np.meshgrid(_x, _y)
x, y = _xx.ravel(), _yy.ravel()
z = np.zeros_like(x)

# Bar heights
dz = [1, 2, 3, 4, 2, 3, 1, 4, 2, 1, 3, 4]

# Create the 3D figure
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plot the 3D bars
ax.bar3d(x, y, z, 1, 1, dz, shade=True)

# Set labels
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.title("3D Bar Plot")
plt.show()

Output:

Conclusion

These examples show how to create various types of 3D plots in Python using Matplotlib.

You can customize these plots further by adjusting parameters like colors, axes labels, and grid points.

3D plotting is a powerful way to visualize complex data and mathematical functions in Python.

Mastering Symbolic Mathematics with SymPy

Mastering Symbolic Mathematics with SymPy

Here’s a sample code using SymPy, a Python library for symbolic mathematics.

We’ll solve a quadratic equation symbolically and also demonstrate differentiation and integration.

Example 1: Solving a Quadratic Equation

Let’s solve the quadratic equation:

x2−5x+6=0

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import sympy as sp

# Define the symbol (variable)
x = sp.symbols('x')

# Define the quadratic equation
equation = x**2 - 5*x + 6

# Solve the equation
solutions = sp.solve(equation, x)

# Print the solutions
print("Solutions to the quadratic equation:")
print(solutions)

Explanation:

  1. Symbol Definition:

    • sp.symbols('x') creates a symbolic variable x.

  2. Equation:

    • We define the quadratic equation x2−5x+6=0.

  3. Solve:

    • sp.solve(equation, x) solves the equation for x and returns the roots (solutions).

  4. Output:

    • The roots of the quadratic equation are printed.

Result:

1
2
Solutions to the quadratic equation:
[2, 3]

Example 2: Differentiation

Let’s find the derivative of the function:

f(x)=x3+2x2−3x+1

Python Code:

1
2
3
4
5
6
7
8
9
# Define the function
f = x**3 + 2*x**2 - 3*x + 1

# Compute the derivative
derivative = sp.diff(f, x)

# Print the derivative
print("The derivative of f(x) is:")
print(derivative)

Explanation:

  1. Function Definition:

    • We define the function f(x)=x3+2x2−3x+1.

  2. Differentiation:

    • sp.diff(f, x) computes the derivative of f with respect to x.

  3. Output:

    • The derivative of the function is printed.

Result:

1
2
The derivative of f(x) is:
3*x**2 + 4*x - 3

Example 3: Integration

Let’s compute the indefinite integral of the function:

f(x)=3x2−4x+5

Python Code:

1
2
3
4
5
6
7
8
9
# Define the function
g = 3*x**2 - 4*x + 5

# Compute the indefinite integral
integral = sp.integrate(g, x)

# Print the integral
print("The indefinite integral of g(x) is:")
print(integral)

Explanation:

  1. Function Definition:

    • We define the function g(x)=3x2−4x+5.

  2. Integration:

    • sp.integrate(g, x) computes the indefinite integral of g with respect to x.

  3. Output:

    • The indefinite integral of the function is printed, including the constant of integration.

Result:

1
2
The indefinite integral of g(x) is:
x**3 - 2*x**2 + 5*x

Conclusion

These examples illustrate how to solve equations, differentiate, and integrate using SymPy.

The library is powerful for symbolic math, allowing you to handle complex mathematical expressions and operations programmatically.

Solving Complex Equations Symbolically Using Python

Solving Complex Equations Symbolically Using Python

To solve a complex mathematical equation in Python, you can use libraries like SymPy for symbolic mathematics or SciPy for numerical methods.

Here’s an example using SymPy to solve a complex symbolic equation.

Example: Solving a Complex Equation

Let’s solve the following complex equation symbolically:

x4+2x3−5x2+3x−7=0

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import sympy as sp

# Define the variable
x = sp.symbols('x')

# Define the complex equation
equation = x**4 + 2*x**3 - 5*x**2 + 3*x - 7

# Solve the equation
solutions = sp.solve(equation, x)

# Print the solutions
print("Solutions to the equation are:")
for solution in solutions:
    print(solution)

Explanation:

  1. SymPy:

    • We use the sympy library for symbolic computation.

  2. Variable Definition:

    • sp.symbols('x') defines x as a symbolic variable.

  3. Equation:

    • We define the equation x4+2x3−5x2+3x−7=0.

  4. Solve:

    • sp.solve(equation, x) solves the equation for x.

  5. Output:

    • The solutions are printed.

Result:

1
2
3
4
5
Solutions to the equation are:
-1/2 + sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3)/2 - sqrt(-18/sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3) - 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 26/3)/2
-1/2 + sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3)/2 + sqrt(-18/sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3) - 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 26/3)/2
-sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3)/2 - 1/2 + sqrt(-2*(-3013/432 + sqrt(134621)/48)**(1/3) + 77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 26/3 + 18/sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3))/2
-sqrt(-2*(-3013/432 + sqrt(134621)/48)**(1/3) + 77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 26/3 + 18/sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3))/2 - sqrt(-77/(18*(-3013/432 + sqrt(134621)/48)**(1/3)) + 2*(-3013/432 + sqrt(134621)/48)**(1/3) + 13/3)/2 - 1/2

For More Complex Equations:

You can solve systems of equations, differential equations, or optimize functions using similar methods in Python, depending on the complexity of your mathematical problem.

graphically solutions

To graphically represent the solutions of the equation, you can plot the function and visually inspect where it crosses the x-axis (i.e., the roots of the equation).

Here’s how you can do it using Matplotlib and NumPy.

Example: Plotting the Complex Equation

We will plot the equation:

f(x)=x4+2x3−5x2+3x−7

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import numpy as np
import matplotlib.pyplot as plt

# Define the function
def f(x):
    return x**4 + 2*x**3 - 5*x**2 + 3*x - 7

# Generate x values
x = np.linspace(-3, 2, 400)

# Calculate y values
y = f(x)

# Plot the function
plt.figure(figsize=(8, 6))
plt.plot(x, y, label=r'$f(x) = x^4 + 2x^3 - 5x^2 + 3x - 7$')
plt.axhline(0, color='black', linewidth=0.5)  # x-axis
plt.axvline(0, color='black', linewidth=0.5)  # y-axis

# Highlight the roots (approximately)
roots = np.roots([1, 2, -5, 3, -7])
for root in roots:
    plt.scatter(root, 0, color='red', zorder=5)
    plt.text(root, 0.5, f'{root:.2f}', color='red')

# Add labels and title
plt.title('Graph of the Equation $f(x) = x^4 + 2x^3 - 5x^2 + 3x - 7$')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()

Explanation:

  1. Function Definition:

    • We define the function f(x)=x4+2x3−5x2+3x−7.

  2. x Values:

    • We generate x values between −3 and 2 to capture the function’s behavior over a wide range.

  3. Plot:

    • We plot the function using plt.plot() and add axes lines with plt.axhline() and plt.axvline() for better visualization.

  4. Roots:

    • We calculate the approximate roots of the equation using np.roots() and plot them as red points on the graph.

  5. Labels and Grid:

    • We add labels, a title, and a grid to make the plot more readable.

Result:

This code will generate a graph showing the function and highlight the roots where the function crosses the x-axis.

The red dots represent the approximate solutions of the equation.

A Basic Guide to Linear Regression Using Statsmodels in Python

A Basic Guide to Linear Regression Using Statsmodels in Python

Here’s a basic useful example of how to use statsmodels for linear regression in Python.

This example demonstrates how to fit a linear regression model, check the summary, and make predictions.

Linear Regression Example with statsmodels

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf

# Generate synthetic data
np.random.seed(42)
n = 100
X = np.random.rand(n)
y = 2 * X + np.random.randn(n) * 0.1  # y = 2*X + noise

# Create a DataFrame
df = pd.DataFrame({
    'X': X,
    'y': y
})

# Add a constant (intercept) to the independent variable
X = sm.add_constant(df['X'])

# Fit the linear regression model
model = sm.OLS(df['y'], X).fit()

# Print the summary of the model
print(model.summary())

# Predict using the model
df['y_pred'] = model.predict(X)

# Print the first few predictions
print(df.head())

# If you prefer using formulas (like in R):
formula = 'y ~ X'
model_formula = smf.ols(formula=formula, data=df).fit()

# Print the summary of the model fitted using formulas
print(model_formula.summary())

Explanation:

  1. Generating Data:

    • We create synthetic data where y is linearly dependent on X with some added noise.

  2. DataFrame:

    • We store the data in a Pandas DataFrame.

  3. Adding a Constant:

    • In linear regression, we often include an intercept.
      sm.add_constant() adds a column of ones to X to account for this.

  4. Fitting the Model:

    • We use sm.OLS() to define the Ordinary Least Squares (OLS) regression model and .fit() to estimate the coefficients.

  5. Summary:

    • model.summary() provides a detailed summary of the model, including R-squared, coefficients, p-values, etc.

  6. Prediction:

    • After fitting the model, we use it to make predictions with .predict().

  7. Formula API:

    • You can also use smf.ols() with a formula string, similar to R’s syntax.

This example covers basic regression, but statsmodels also offers more advanced models like time series analysis (ARIMA), logistic regression, and more.

Explanation of the output

Output:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.976
Model:                            OLS   Adj. R-squared:                  0.976
Method:                 Least Squares   F-statistic:                     4065.
Date:                Sun, 25 Aug 2024   Prob (F-statistic):           1.35e-81
Time:                        23:46:40   Log-Likelihood:                 99.112
No. Observations:                 100   AIC:                            -194.2
Df Residuals:                      98   BIC:                            -189.0
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0215      0.017      1.263      0.210      -0.012       0.055
X              1.9540      0.031     63.754      0.000       1.893       2.015
==============================================================================
Omnibus:                        0.900   Durbin-Watson:                   2.285
Prob(Omnibus):                  0.638   Jarque-Bera (JB):                0.808
Skew:                           0.217   Prob(JB):                        0.668
Kurtosis:                       2.929   Cond. No.                         4.18
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
          X         y    y_pred
0  0.374540  0.757785  0.753370
1  0.950714  1.871528  1.879227
2  0.731994  1.473164  1.451842
3  0.598658  0.998560  1.191302
4  0.156019  0.290070  0.326374
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.976
Model:                            OLS   Adj. R-squared:                  0.976
Method:                 Least Squares   F-statistic:                     4065.
Date:                Sun, 25 Aug 2024   Prob (F-statistic):           1.35e-81
Time:                        23:46:40   Log-Likelihood:                 99.112
No. Observations:                 100   AIC:                            -194.2
Df Residuals:                      98   BIC:                            -189.0
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      0.0215      0.017      1.263      0.210      -0.012       0.055
X              1.9540      0.031     63.754      0.000       1.893       2.015
==============================================================================
Omnibus:                        0.900   Durbin-Watson:                   2.285
Prob(Omnibus):                  0.638   Jarque-Bera (JB):                0.808
Skew:                           0.217   Prob(JB):                        0.668
Kurtosis:                       2.929   Cond. No.                         4.18
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

This output is the summary of an Ordinary Least Squares (OLS) linear regression model.

Let’s break down the key parts of the output:

1. Model Information

  • Dep. Variable: y

    • The dependent variable being predicted (in this case, y).

  • Model: OLS

    • The type of model used (Ordinary Least Squares regression).

  • Method: Least Squares

    • The method used to estimate the coefficients of the model.

  • No. Observations: 100

    • The number of observations (data points) used in the model.

  • Df Residuals: 98

    • The degrees of freedom of the residuals (number of observations minus the number of estimated parameters, including the intercept).

  • Df Model: 1

    • The degrees of freedom of the model (number of estimated parameters excluding the intercept).

2. Statistical Measures

  • R-squared: 0.976

    • This is the coefficient of determination.
      It indicates that 97.6% of the variance in the dependent variable y is explained by the independent variable X.
      A value close to 1 indicates a good fit.

  • Adj. R-squared: 0.976

    • The adjusted R-squared accounts for the number of predictors in the model.
      It’s also high, which confirms the model fits well.

  • F-statistic: 4065.0

    • This is the test statistic for the overall significance of the model.
      A high F-statistic suggests that the model is statistically significant.

  • Prob (F-statistic): 1.35e-81

    • The p-value associated with the F-statistic. A very small value (much less than 0.05) indicates strong evidence against the null hypothesis, suggesting that the model is statistically significant.

  • Log-Likelihood: 99.112

    • A measure of model fit. Higher values indicate a better fit.

  • AIC (Akaike Information Criterion): -194.2

    • A lower AIC suggests a better model.
      It balances model fit with the number of parameters to avoid overfitting.

  • BIC (Bayesian Information Criterion): -189.0

    • Similar to AIC but with a stronger penalty for models with more parameters.
      Lower is better.

3. Coefficients Table

  • coef:

    • The estimated coefficients for the model.
    • const: The intercept is 0.0215.
    • X: The slope is 1.9540, meaning that for every one unit increase in X, y increases by about 1.954 units.

  • std err:

    • The standard error of the coefficient estimate.
      Smaller values indicate more precise estimates.

  • t:

    • The t-statistic for the hypothesis test that the coefficient is zero.
      For X, it is 63.754, indicating that X is a significant predictor.

  • P>|t|:

    • The p-value for the t-test.
      A p-value less than 0.05 indicates that the coefficient is significantly different from zero.
    • For X, the p-value is 0.000, indicating it is highly significant.

  • [0.025, 0.975]:

    • The 95% confidence interval for the coefficients.
      For X, the true slope is likely between 1.893 and 2.015.

4. Model Diagnostics

  • Omnibus: 0.900, Prob(Omnibus): 0.638

    • These tests check for normality of the residuals.
      A p-value greater than 0.05 suggests that the residuals are normally distributed (which is good).

  • Jarque-Bera (JB): 0.808, Prob(JB): 0.668

    • Another test for normality.
      Similar to the Omnibus test, a p-value above 0.05 indicates that the residuals follow a normal distribution.

  • Skew: 0.217

    • The skewness of the residuals.
      A value close to zero suggests symmetry.

  • Kurtosis: 2.929

    • Kurtosis measures the “tailedness” of the distribution. A value close to 3 indicates normal kurtosis (similar to a normal distribution).

  • Durbin-Watson: 2.285

    • This statistic tests for autocorrelation in the residuals.
      A value around 2 suggests that there is no autocorrelation (which is good).

  • Cond. No.: 4.18

    • The condition number tests for multicollinearity.
      Values above 30 may indicate problematic multicollinearity, but 4.18 is quite low, indicating no issues here.

5. Predictions

  • y_pred:
    • These are the predicted values of y based on the fitted model.
      The table at the bottom shows the first few predictions alongside the actual y values and the X values.

Conclusion:

This linear regression model fits the data well, with a high R-squared and statistically significant coefficients.

The residuals appear to be normally distributed, and there is no evidence of autocorrelation or multicollinearity.

Advanced Data Visualization with Seaborn

Advanced Data Visualization with Seaborn: Exploring the Iris Dataset in Python

Here’s a complex Seaborn sample that involves advanced visualizations and data manipulation.

The code uses a combination of pairplot, violin plot, and swarm plot to visualize complex relationships in the data.

This example uses the famous “Iris” dataset for visualizing species relationships based on different features.

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris

# Load the Iris dataset
iris_data = load_iris()
df = pd.DataFrame(data=iris_data['data'], columns=iris_data['feature_names'])
df['species'] = pd.Categorical.from_codes(iris_data.target, iris_data.target_names)

# Pairplot to visualize pairwise relationships in the dataset
sns.pairplot(df, hue='species', palette='husl')
plt.suptitle("Pairplot of Iris Dataset", y=1.02)
plt.show()

# Violin plot to visualize the distribution of sepal length by species
plt.figure(figsize=(10, 6))
sns.violinplot(x='species', y='sepal length (cm)', data=df, inner=None, palette='pastel')
sns.swarmplot(x='species', y='sepal length (cm)', data=df, color='k', alpha=0.5)
plt.title("Violin Plot of Sepal Length by Species")
plt.show()

# Heatmap to visualize correlation between the features
plt.figure(figsize=(8, 6))
correlation_matrix = df.iloc[:, :-1].corr()
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
plt.title("Heatmap of Feature Correlations in Iris Dataset")
plt.show()

# PairGrid for a more customized visualization
g = sns.PairGrid(df, hue='species', palette='viridis')
g.map_diag(sns.histplot)
g.map_offdiag(sns.scatterplot)
g.add_legend()
plt.suptitle("Custom PairGrid of Iris Dataset", y=1.02)
plt.show()

Explanation:

  1. Pairplot:
    This visualizes pairwise relationships across the dataset’s features, coloring the points by species.
  2. Violin Plot with Swarm Plot Overlay:
    This shows the distribution of sepal lengths across different species while overlaying individual data points for clarity.
  3. Heatmap:
    Displays the correlation between different features, with annotations to highlight the correlation values.
  4. PairGrid:
    A more customizable version of pairplot that allows you to control individual plots for both the diagonal and off-diagonal elements.

Output:

  • A pairplot with different species colored differently.

  • A violin plot with swarm plot overlay, showing the distribution of sepal length.

  • A heatmap with correlation values for the features.

  • A custom PairGrid with scatter plots and histograms.

Exploring Complex Data Relationships with Seaborn

Exploring Complex Data Relationships with Seaborn

Here’s a complex example using Seaborn, which involves creating a pair of visualizations:

a PairGrid with different types of plots and a FacetGrid to explore the relationships within a dataset.

We’ll use the Seaborn Tips dataset to demonstrate this.

1. PairGrid with Multiple Plot Types

In this example, we’ll visualize relationships between different pairs of features in the dataset using different types of plots on a grid.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import seaborn as sns
import matplotlib.pyplot as plt

# Load the Tips dataset
tips = sns.load_dataset("tips")

# Create a PairGrid with different types of plots
g = sns.PairGrid(tips, hue="smoker")
g.map_diag(sns.histplot)
g.map_offdiag(sns.scatterplot)
g.add_legend()

# Show the plot
plt.show()

[Output]

2. FacetGrid for Complex Plotting

In this example, we’ll use Seaborn′s FacetGrid to plot multiple subplots based on categorical variables.

1
2
3
4
5
6
7
8
9
10
11
12
13
import seaborn as sns
import matplotlib.pyplot as plt

# Load the Tips dataset
tips = sns.load_dataset("tips")

# Create a FacetGrid to visualize the data
g = sns.FacetGrid(tips, col="time", row="sex", hue="smoker", margin_titles=True)
g.map(sns.scatterplot, "total_bill", "tip")
g.add_legend()

# Show the plot
plt.show()

[Output]

Explanation:

  • PairGrid with Multiple Plot Types:
    The PairGrid creates a grid of plots where each diagonal element shows the distribution of a single feature, and the off-diagonal elements show the relationship between pairs of features.
    We used histplot for the diagonal and scatterplot for the off-diagonal.

  • FacetGrid for Complex Plotting:
    The FacetGrid allows us to create subplots based on the values of categorical variables.
    Here, we create a grid of scatter plots showing the relationship between total_bill and tip for different combinations of time, sex, and smoker.

These examples show how you can create complex visualizations that reveal intricate patterns in the data.

Möbius strip in Python

Möbius strip in Python

Let’s create a complex 3D graph using Plotly.

This time, we’ll generate and visualize a 3D parametric surface plot known as a Möbius strip.

A Möbius strip is a non-orientable surface with only one side and one edge.

Here’s the Python code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np
import plotly.graph_objects as go

# Define the parametric equations for a Möbius strip
theta = np.linspace(0, 2 * np.pi, 100)
w = np.linspace(-0.5, 0.5, 50)
theta, w = np.meshgrid(theta, w)

# Parametric equations for the Möbius strip
x = (1 + w * np.cos(theta / 2)) * np.cos(theta)
y = (1 + w * np.cos(theta / 2)) * np.sin(theta)
z = w * np.sin(theta / 2)

# Create a 3D surface plot for the Möbius strip
fig = go.Figure(data=[go.Surface(x=x, y=y, z=z, colorscale='Viridis')])

# Customize the layout
fig.update_layout(
    title='3D Möbius Strip',
    scene=dict(
        xaxis_title='X Axis',
        yaxis_title='Y Axis',
        zaxis_title='Z Axis',
        aspectratio=dict(x=1, y=1, z=0.3),
        camera=dict(eye=dict(x=1.25, y=1.25, z=0.6))
    ),
    autosize=False,
    width=800,
    height=800,
    margin=dict(l=65, r=50, b=65, t=90)
)

# Show the plot
fig.show()

Explanation:

  • Möbius Strip Geometry: The Möbius strip is generated using parametric equations. The theta variable controls the circular angle around the strip, while w controls the width of the strip.
  • Surface Plot: A 3D surface plot is created using the go.Surface function in Plotly. The x, y, and z arrays define the coordinates of the surface.
  • Customization: The plot layout is customized with axis labels, aspect ratio, and a camera angle to better visualize the 3D structure.

This interactive 3D plot allows you to explore the Möbius strip’s fascinating geometry by rotating, zooming, and panning the view.

The use of a color gradient further enhances the visual appeal.

Output:

Optimizing Supply Chain Logistics with Python

Optimizing Supply Chain Logistics with Python: A Real-World Example

Let’s solve a realistic supply chain optimization problem using Python and the PuLP library.

The goal is to minimize the total cost of transporting goods from multiple warehouses to multiple stores while considering supply and demand constraints.

Problem Statement:

  • We have 3 warehouses, each with a limited supply of goods.
  • We have 5 stores, each with a specific demand for goods.
  • Transportation costs between warehouses and stores are given.
  • We want to determine the optimal number of goods to transport from each warehouse to each store to minimize the total transportation cost.

Python Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import pulp as pl

# Define the problem
problem = pl.LpProblem("Supply_Chain_Optimization", pl.LpMinimize)

# Warehouses and their supplies
warehouses = ["W1", "W2", "W3"]
supply = {"W1": 100, "W2": 150, "W3": 200}

# Stores and their demands
stores = ["S1", "S2", "S3", "S4", "S5"]
demand = {"S1": 80, "S2": 70, "S3": 90, "S4": 60, "S5": 100}

# Transportation costs (in dollars) between warehouses and stores
costs = {
    ("W1", "S1"): 4, ("W1", "S2"): 6, ("W1", "S3"): 9, ("W1", "S4"): 5, ("W1", "S5"): 10,
    ("W2", "S1"): 3, ("W2", "S2"): 8, ("W2", "S3"): 7, ("W2", "S4"): 4, ("W2", "S5"): 6,
    ("W3", "S1"): 5, ("W3", "S2"): 4, ("W3", "S3"): 6, ("W3", "S4"): 3, ("W3", "S5"): 7
}

# Decision variables: number of goods transported from warehouse i to store j
transport = pl.LpVariable.dicts("Transport", [(w, s) for w in warehouses for s in stores], lowBound=0, cat='Continuous')

# Objective function: Minimize the total transportation cost
problem += pl.lpSum(transport[w, s] * costs[w, s] for w in warehouses for s in stores)

# Constraints: Ensure that the total goods transported from each warehouse does not exceed its supply
for w in warehouses:
    problem += pl.lpSum(transport[w, s] for s in stores) <= supply[w], f"Supply_Constraint_{w}"

# Constraints: Ensure that the total goods transported to each store meets its demand
for s in stores:
    problem += pl.lpSum(transport[w, s] for w in warehouses) == demand[s], f"Demand_Constraint_{s}"

# Solve the problem
problem.solve()

# Display the results
print(f"Status: {pl.LpStatus[problem.status]}")
for w in warehouses:
    for s in stores:
        if transport[w, s].varValue > 0:
            print(f"Transport {transport[w, s].varValue} units from {w} to {s}")

print(f"Total Cost: ${pl.value(problem.objective)}")

Explanation:

  • The code defines a linear programming problem using PuLP, where the objective is to minimize the transportation costs.
  • We define the decision variables, objective function, and constraints, and then solve the problem using the solve() method.
  • Finally, the code prints the optimal transportation plan and the total cost.

This example solves a supply chain optimization problem with realistic constraints, demonstrating the power of Python in handling such tasks.

Explanation of Results

1
2
3
4
5
6
7
8
9
Status: Optimal
Transport 30.0 units from W1 to S1
Transport 20.0 units from W1 to S4
Transport 50.0 units from W2 to S1
Transport 100.0 units from W2 to S5
Transport 70.0 units from W3 to S2
Transport 90.0 units from W3 to S3
Transport 40.0 units from W3 to S4
Total Cost: $1910.0

The result indicates that the supply chain optimization problem was successfully solved, and the solution is optimal.

Here’s a detailed explanation of the output:

Status: Optimal

This means that the solver found the best possible solution, minimizing the total transportation cost while satisfying all constraints (supply and demand).

Transportation Plan:

  • Transport 30.0 units from W1 to S1: Warehouse W1 will send 30 units of goods to Store S1.
  • Transport 20.0 units from W1 to S4: Warehouse W1 will send 20 units of goods to Store S4.
  • Transport 50.0 units from W2 to S1: Warehouse W2 will send 50 units of goods to Store S1.
  • Transport 100.0 units from W2 to S5: Warehouse W2 will send 100 units of goods to Store S5.
  • Transport 70.0 units from W3 to S2: Warehouse W3 will send 70 units of goods to Store S2.
  • Transport 90.0 units from W3 to S3: Warehouse W3 will send 90 units of goods to Store S3.
  • Transport 40.0 units from W3 to S4: Warehouse W3 will send 40 units of goods to Store S4.

Total Cost: $1910.0

The total transportation cost for moving the goods from all the warehouses to the stores, based on the above transportation plan, is $1910.

Interpretation:

  • The solution satisfies all the supply constraints (ensuring that no warehouse ships more than its available supply) and all the demand constraints (ensuring that each store receives the exact amount it needs).
  • The total transportation cost of $1910 is the minimum possible cost given the constraints and transportation costs between warehouses and stores.