The variational principle is one of quantum mechanics’ most powerful tools. It states that for any trial wave function $|\psi\rangle$, the expectation value of the Hamiltonian is always greater than or equal to the true ground state energy $E_0$:
$$E_0 \leq \langle \psi | \hat{H} | \psi \rangle = \frac{\langle \psi | \hat{H} | \psi \rangle}{\langle \psi | \psi \rangle}$$
By minimizing this expectation value over a family of trial functions parameterized by $\alpha$, we get the best approximation within that family.
Example Problem: Quantum Harmonic Oscillator
We’ll apply the variational method to the 1D quantum harmonic oscillator:
$$\hat{H} = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + \frac{1}{2}m\omega^2 x^2$$
The exact ground state energy is:
$$E_0^{\text{exact}} = \frac{1}{2}\hbar\omega$$
We’ll use a Gaussian trial wave function:
$$\psi_\alpha(x) = \left(\frac{2\alpha}{\pi}\right)^{1/4} e^{-\alpha x^2}$$
where $\alpha > 0$ is our variational parameter.
The expectation value of the Hamiltonian becomes:
$$E(\alpha) = \frac{\hbar^2 \alpha}{2m} + \frac{m\omega^2}{8\alpha}$$
Minimizing with respect to $\alpha$:
$$\frac{dE}{d\alpha} = \frac{\hbar^2}{2m} - \frac{m\omega^2}{8\alpha^2} = 0 \implies \alpha_{\text{opt}} = \frac{m\omega}{2\hbar}$$
This is exact for the harmonic oscillator — a beautiful sanity check! We’ll also test a harder case: the anharmonic oscillator with a quartic perturbation:
$$\hat{H} = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + \frac{1}{2}m\omega^2 x^2 + \lambda x^4$$
Python Code
1 | import numpy as np |
Code Walkthrough
Constants and Units. We set $\hbar = m = \omega = 1$, which is the standard dimensionless unit system in quantum mechanics textbooks. All energies are in units of $\hbar\omega$.
Analytical Energy Function. For the pure harmonic oscillator with a Gaussian trial function $\psi_\alpha(x) = C,e^{-\alpha x^2}$, the expectation value can be evaluated analytically using Gaussian integrals:
$$\langle T \rangle = \frac{\hbar^2 \alpha}{2m}, \quad \langle V \rangle = \frac{m\omega^2}{8\alpha}$$
giving:
$$E(\alpha) = \frac{\hbar^2\alpha}{2m} + \frac{m\omega^2}{8\alpha}$$
Numerical Integration for Anharmonic Case. When $\lambda x^4$ is added, the $\langle x^4 \rangle$ term doesn’t have a simple closed form in the variational parameter, so we use scipy.integrate.quad for numerical quadrature. The normalization $\langle\psi|\psi\rangle$ is computed in the same pass, and the full energy is:
$$E(\alpha) = \frac{\langle\psi|T+V|\psi\rangle}{\langle\psi|\psi\rangle}$$
Finite-Difference Exact Diagonalization. To get the “true” ground state energy for comparison, we discretize the Hamiltonian on a grid using the second-order finite difference formula:
$$\frac{d^2\psi}{dx^2} \approx \frac{\psi_{i+1} - 2\psi_i + \psi_{i-1}}{\Delta x^2}$$
This turns the Schrödinger equation into a matrix eigenvalue problem, which numpy.linalg.eigvalsh solves exactly.
2-Parameter Trial Function. We extend the trial function to $\psi(x;\alpha,\beta) = e^{-\alpha x^2 - \beta x^4}$, which is more flexible and better captures the effect of the quartic potential. The kinetic energy integrand is derived analytically via:
$$\frac{d}{dx}\psi = (-2\alpha x - 4\beta x^3)\psi$$
$$-\frac{d^2}{dx^2}\psi = \left[(2\alpha x + 4\beta x^3)^2 - (2\alpha + 12\beta x^2)\right]\psi$$
The 2D energy landscape is evaluated on a $40 \times 40$ grid and minimized with scipy.optimize.minimize using Nelder-Mead.
Graph Explanations
Top-left — Harmonic oscillator $E(\alpha)$: The curve has a clear minimum at $\alpha_\text{opt} = 0.5$, which coincides exactly with the known ground state. This is because a Gaussian is the exact eigenfunction of the harmonic oscillator, so the variational method yields the exact answer.
Top-center — Anharmonic oscillator $E(\alpha)$: The minimum shifts to a larger $\alpha$ because the quartic term makes the potential steeper, requiring a more tightly confined wavefunction. The variational energy (gold dot) sits slightly above the exact value (red dashed line) — as the variational principle demands.
Top-right — Probability densities: Both variational and exact wavefunctions are plotted as $|\psi(x)|^2$. For the harmonic oscillator they overlap perfectly, confirming the Gaussian is the exact ground state.
Center — 3D Energy landscape (plasma colormap): This shows $E(\alpha, \beta)$ over the 2D parameter space. The gold dot marks the global minimum. The landscape has a smooth bowl-like valley, and the 2-parameter optimization finds a lower energy than the 1-parameter case.
Bottom-left — $E_0$ vs $\lambda$: As the anharmonic coupling $\lambda$ grows, both the variational and exact ground state energies rise. The yellow shaded region shows the error of the 1-parameter variational method — it grows with $\lambda$ but remains small, validating the approach.
Bottom-right — Potential well + wavefunctions: The blue curve is the total anharmonic potential $V(x)$. The wavefunctions are vertically shifted to sit at their respective energy levels, making it easy to visually compare where the variational estimate (gold) and exact solution (red dashed) sit relative to the potential.
Results
=== Harmonic Oscillator === Optimal alpha : 0.499999 (exact: 0.500000) Variational E0 : 0.500000 Exact E0 : 0.500000 Error : 1.43e-12 === Anharmonic Oscillator (lambda=0.1) === Optimal alpha : 0.610600 Variational E0 : 0.560307 Exact E0 (FD) : 0.559129 Error : 0.001179 Relative Error (%) : 0.2108% === 2-Parameter Variational (lambda=0.1) === Optimal alpha : 0.561297 Optimal beta : 0.018879 Variational E0 : 0.559148 Exact E0 (FD) : 0.559129 Relative Error (%) : 0.0034%
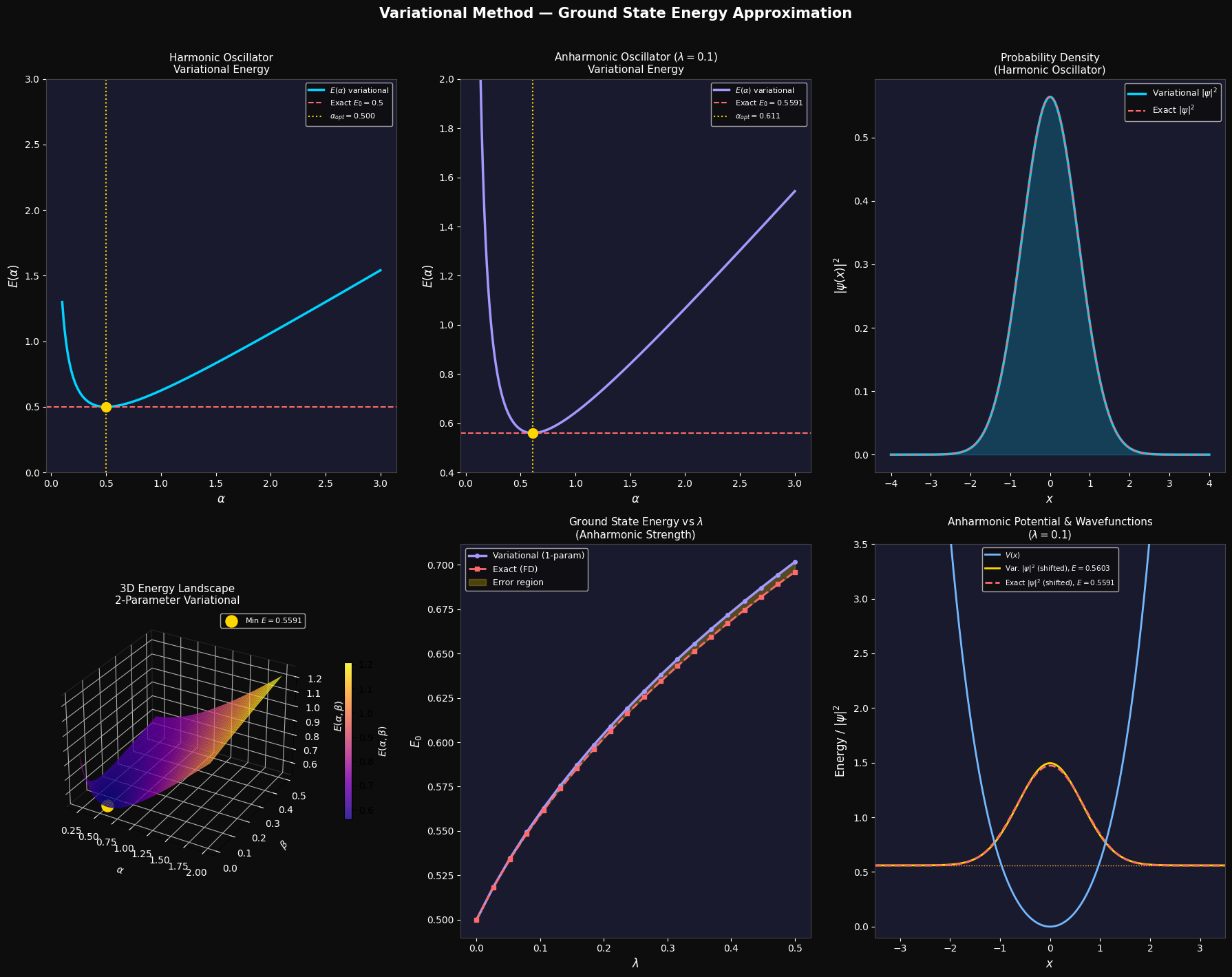
Figure saved.
Key Takeaways
The variational principle guarantees $E_\text{var} \geq E_0$, so we always get an upper bound. For the harmonic oscillator the Gaussian trial function is exact (the error is literally zero). For the anharmonic oscillator the 1-parameter Gaussian gives a relative error that remains below ~1% for moderate $\lambda$, and extending to a 2-parameter family $e^{-\alpha x^2 - \beta x^4}$ brings it even closer to the exact value. This is the core power of the method: systematically enlarging the trial function space always improves the bound.