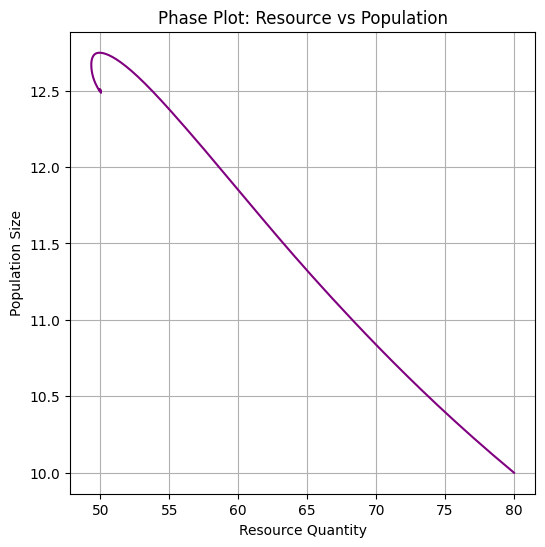
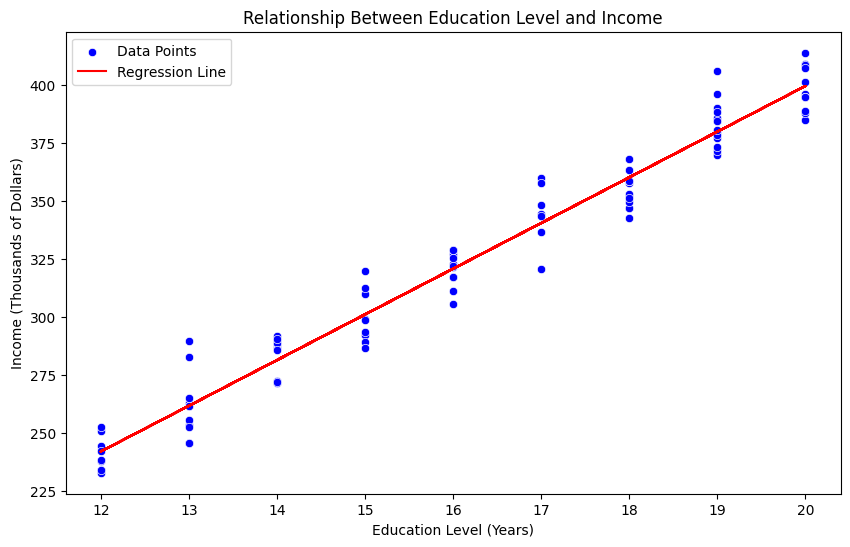
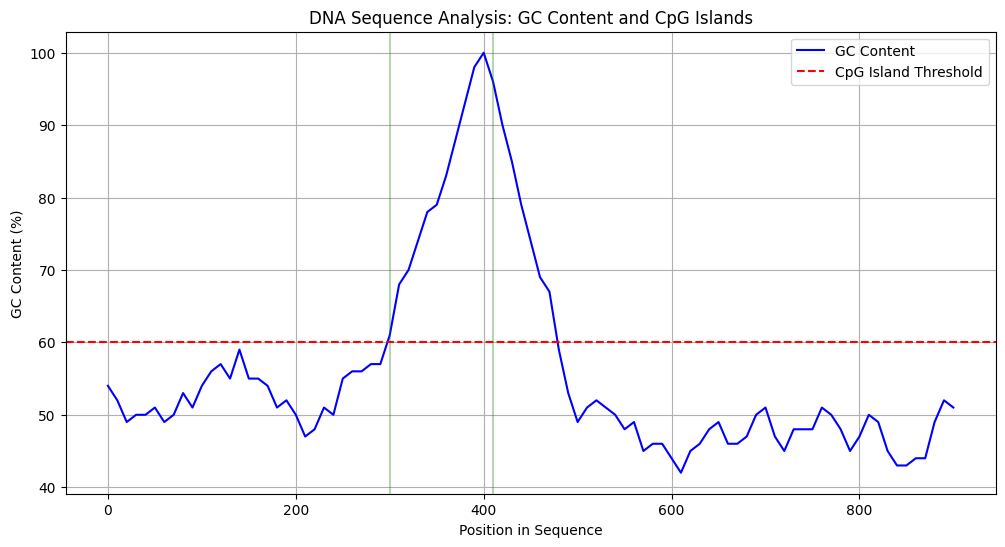
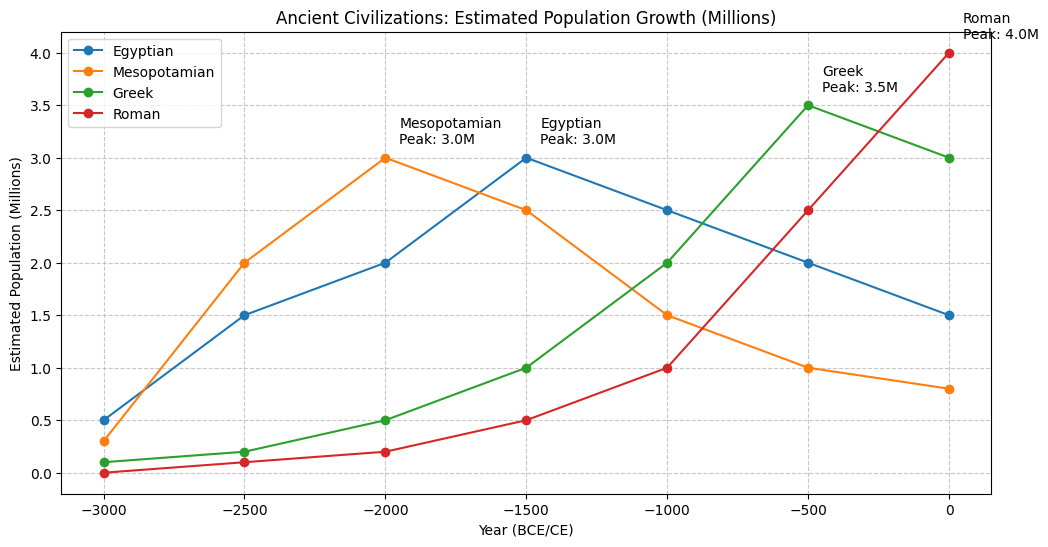
I’ll create an environmental science example analyzing the relationship between CO2 emissions and global temperature changes, then visualize the data.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

# Generate sample data (simplified model)
years = np.arange(1970, 2021)
# Simulate CO2 emissions with increasing trend and some random variation
co2_emissions = 15000 + (years - 1970) * 300 + np.random.normal(0, 500, len(years))
# Simulate temperature anomalies with correlation to CO2
base_temp = 14.0  # base temperature in Celsius
temp_anomalies = (co2_emissions - co2_emissions[0]) * 0.0001 + np.random.normal(0, 0.1, len(years))

# Create DataFrame
climate_data = pd.DataFrame({
    'Year': years,
    'CO2_Emissions': co2_emissions,
    'Temperature_Anomaly': temp_anomalies
})

# Calculate correlation coefficient
correlation = stats.pearsonr(climate_data['CO2_Emissions'], climate_data['Temperature_Anomaly'])

# Calculate simple linear regression
slope, intercept = np.polyfit(climate_data['CO2_Emissions'], climate_data['Temperature_Anomaly'], 1)
regression_line = slope * climate_data['CO2_Emissions'] + intercept

# Create visualization
plt.figure(figsize=(12, 8))

# Plot 1: CO2 Emissions over time
plt.subplot(2, 1, 1)
plt.plot(climate_data['Year'], climate_data['CO2_Emissions'], 'b-', label='CO2 Emissions')
plt.title('Annual CO2 Emissions (1970-2020)')
plt.xlabel('Year')
plt.ylabel('CO2 Emissions (Million Metric Tons)')
plt.grid(True)
plt.legend()

# Plot 2: Temperature Anomaly vs CO2 Emissions with regression line
plt.subplot(2, 1, 2)
plt.scatter(climate_data['CO2_Emissions'], climate_data['Temperature_Anomaly'], 
           alpha=0.5, label='Temperature vs CO2')
plt.plot(climate_data['CO2_Emissions'], regression_line, 'r-', 
         label=f'Regression Line (slope: {slope:.2e})')
plt.title('Temperature Anomaly vs CO2 Emissions')
plt.xlabel('CO2 Emissions (Million Metric Tons)')
plt.ylabel('Temperature Anomaly (°C)')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

# Print analysis results
print(f"Correlation coefficient: {correlation[0]:.3f}")
print(f"P-value: {correlation[1]:.3e}")
print(f"Regression slope: {slope:.2e} °C/MtCO2")

Let me explain this environmental science example:

1. Problem Statement:
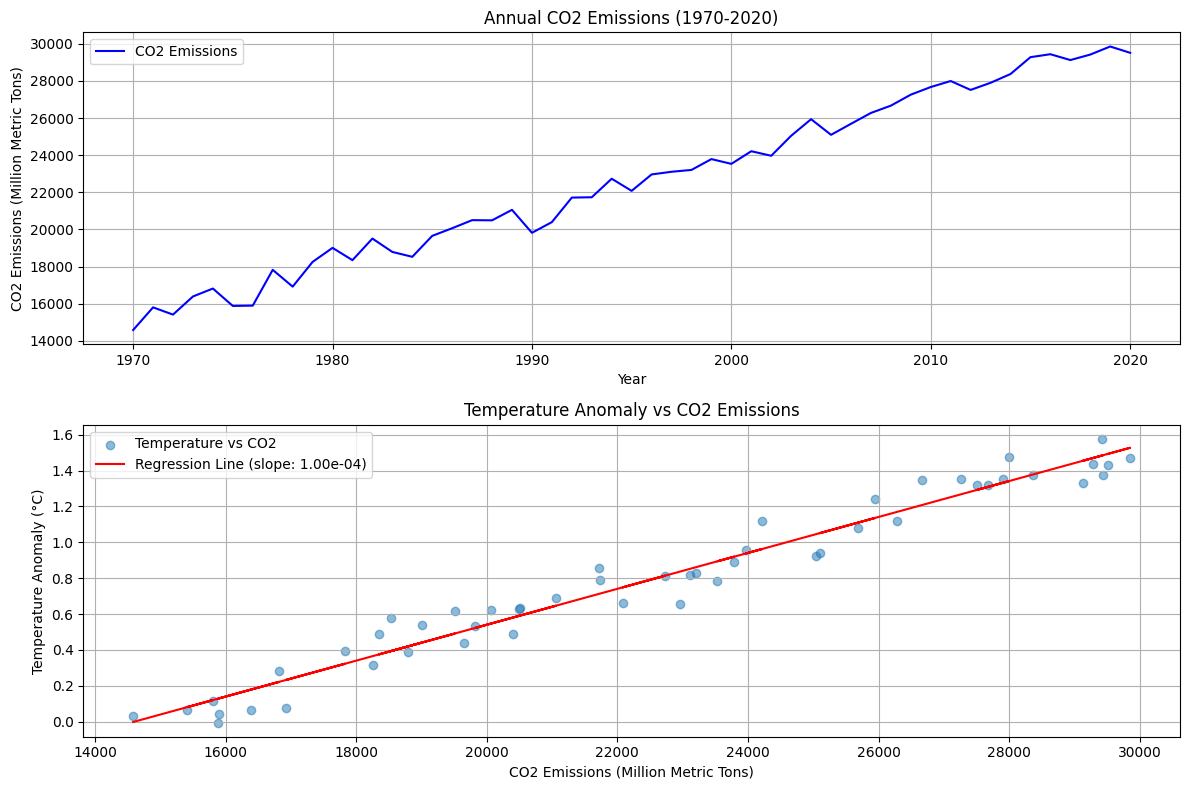
   We’re analyzing the relationship between CO2 emissions and global temperature changes over a 50-year period (1970-2020).

2. Data Simulation:

• We create synthetic data that mimics real-world patterns
• CO2 emissions show an increasing trend with random variations
• Temperature anomalies are modeled with a correlation to CO2 emissions

3. Analysis Components:

• Correlation analysis between CO2 and temperature
• Linear regression to quantify the relationship
• Visualization of trends and relationships

4. Visualization:
   The code creates two plots:

• Top plot: Shows CO2 emissions trend over time
• Bottom plot: Displays the relationship between temperature anomalies and CO2 emissions, including a regression line

5. Key Features:

• Error handling with random variations
• Statistical analysis (correlation coefficient and p-value)
• Clear visualization with proper labeling and grid lines

When you run this code, you’ll see:

• A clear upward trend in CO2 emissions over time
• A positive correlation between CO2 emissions and temperature anomalies
• Statistical measures of the relationship strength

Correlation coefficient: 0.981
P-value: 2.097e-36
Regression slope: 1.00e-04 °C/MtCO2

I’ll create a sports science example analyzing sprint performance data and demonstrate how to process and visualize it using Python.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

# Generate sample data for 10 athletes over 5 training sessions
np.random.seed(42)
n_athletes = 10
n_sessions = 5

# Create sprint times data (100m sprint)
athlete_names = [f"Athlete_{i+1}" for i in range(n_athletes)]
sessions = [f"Session_{i+1}" for i in range(n_sessions)]

# Generate realistic sprint times (between 10.5 and 11.5 seconds)
# With slight improvement trend over sessions
base_times = np.random.uniform(10.5, 11.5, n_athletes)
sprint_times = np.array([
    [time - (session * 0.05) + np.random.normal(0, 0.1) 
     for session in range(n_sessions)]
    for time in base_times
])

# Create DataFrame
df = pd.DataFrame(sprint_times, 
                 index=athlete_names,
                 columns=sessions)

# Calculate statistics
session_means = df.mean()
session_stds = df.std()
improvement = df['Session_1'] - df['Session_5']  # Total improvement

# Perform statistical analysis
ttest_result = stats.ttest_rel(df['Session_1'], df['Session_5'])

# Create visualizations
plt.figure(figsize=(15, 10))

# Plot 1: Sprint times over sessions
plt.subplot(2, 2, 1)
for athlete in df.index:
    plt.plot(sessions, df.loc[athlete], marker='o', label=athlete)
plt.title('Sprint Times Progression')
plt.xlabel('Training Session')
plt.ylabel('Time (seconds)')
plt.grid(True)

# Plot 2: Box plot of sprint times
plt.subplot(2, 2, 2)
df.boxplot()
plt.title('Distribution of Sprint Times')
plt.xlabel('Training Session')
plt.ylabel('Time (seconds)')

# Plot 3: Mean times with error bars
plt.subplot(2, 2, 3)
plt.errorbar(sessions, session_means, yerr=session_stds, 
            marker='o', capsize=5, capthick=2)
plt.title('Mean Sprint Times with Standard Deviation')
plt.xlabel('Training Session')
plt.ylabel('Time (seconds)')
plt.grid(True)

# Plot 4: Individual improvements
plt.subplot(2, 2, 4)
improvement.sort_values().plot(kind='bar')
plt.title('Total Improvement by Athlete')
plt.xlabel('Athlete')
plt.ylabel('Time Improvement (seconds)')
plt.grid(True)

plt.tight_layout()
plt.show()

# Print statistical summary
print("\nStatistical Summary:")
print("===================")
print(f"Mean initial time: {df['Session_1'].mean():.2f} seconds")
print(f"Mean final time: {df['Session_5'].mean():.2f} seconds")
print(f"Average improvement: {improvement.mean():.2f} seconds")
print(f"\nPaired t-test results:")
print(f"t-statistic: {ttest_result.statistic:.3f}")
print(f"p-value: {ttest_result.pvalue:.3f}")

Let me explain this sports science example that analyzes sprint performance:

1. Data Generation and Setup:

   • We simulate data for 10 athletes over 5 training sessions
   • Sprint times are generated between 10.5 and 11.5 seconds (realistic 100m sprint times)
   • We include a slight improvement trend and random variation

2. Analysis Components:

   • Tracking individual athlete progression
   • Calculating statistical measures (mean, standard deviation)
   • Measuring total improvement
   • Performing a paired t-test to check if improvement is statistically significant

3. Visualizations:

The code creates four different plots:

• Line plot showing each athlete’s progression
• Box plot showing the distribution of times in each session
• Mean times with error bars showing variation
• Bar chart showing total improvement by athlete

4. Statistical Output:

Statistical Summary:
===================
Mean initial time: 10.95 seconds
Mean final time: 10.81 seconds
Average improvement: 0.14 seconds

Paired t-test results:
t-statistic: 3.765
p-value: 0.004

• Calculates mean initial and final times
• Shows average improvement across all athletes
• Performs statistical significance testing

The visualizations help coaches and athletes:

• Track individual and group progress
• Identify outliers or unusual patterns
• Understand the variation in performance
• Quantify improvements over time

This analysis could be extended to include:

• More advanced metrics like acceleration phases
• Fatigue analysis
• Correlation with other training parameters
• Prediction of future performance

Let’s consider a medical example where we analyze the growth of a tumor over time.

We’ll use Python to model the tumor growth, solve the differential equation, and visualize the results.

Problem Statement

The growth of a tumor can often be modeled using the Gompertz growth model, which is given by the differential equation:

dVdt=aVln(KV)

• V(t) is the volume of the tumor at time t.
• a is the growth rate of the tumor.
• K is the carrying capacity, i.e., the maximum volume the tumor can reach.

Python Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# Define the Gompertz growth model
def gompertz_growth(t, V, a, K):
    return a * V * np.log(K / V)

# Parameters
a = 0.1  # Growth rate
K = 1000  # Carrying capacity (maximum tumor volume)
V0 = 10  # Initial tumor volume

# Time span for the solution
t_span = (0, 50)  # From t=0 to t=50
t_eval = np.linspace(t_span[0], t_span[1], 300)  # Points where the solution is evaluated

# Solve the differential equation
sol = solve_ivp(gompertz_growth, t_span, [V0], args=(a, K), t_eval=t_eval, method='RK45')

# Extract the solution
V = sol.y[0]

# Plot the results
plt.figure(figsize=(10, 6))
plt.plot(sol.t, V, label='Tumor Volume (V)', color='b')
plt.xlabel('Time (t)')
plt.ylabel('Tumor Volume (V)')
plt.title('Tumor Growth Over Time (Gompertz Model)')
plt.legend()
plt.grid(True)
plt.show()

Explanation

1. Gompertz Growth Model:

The differential equation dVdt=aVln(KV) is implemented in the gompertz_growth function.
This function takes the current time t, the current tumor volume V, and the parameters a and K to compute the rate of change of the tumor volume.

2. Parameters:

   • a = 0.1: This is the growth rate of the tumor.
   • K = 1000: This is the carrying capacity, the maximum volume the tumor can reach.
   • V0 = 10: This is the initial volume of the tumor at time t=0.

3. Solving the Differential Equation:

We use solve_ivp from scipy.integrate to solve the differential equation.
The method RK45 is a Runge-Kutta method of order 5(4), which is suitable for solving non-stiff differential equations.

4. Plotting the Results:

The tumor volume V is plotted against time t.
The plot shows how the tumor volume grows over time, approaching the carrying capacity K.

Graph Interpretation

• The tumor volume starts at V0 = 10 and grows rapidly at first.
• As the tumor volume approaches the carrying capacity K = 1000, the growth rate slows down.
• The tumor volume asymptotically approaches the carrying capacity, but never exceeds it.

This model is useful in oncology for understanding tumor growth dynamics and planning treatment strategies.

Output

The output will be a graph showing the tumor volume V over time t.

The curve will start at V0 = 10 and gradually approach K = 1000, illustrating the Gompertz growth behavior.

Let’s solve an environmental science problem using Python.

We will model Population Dynamics and Resource Consumption, a crucial topic in environmental science to understand sustainability and ecological balance.

Problem Statement

We want to simulate the interactions between a population and a renewable resource:

• A population consumes a natural resource for survival.
• The resource regenerates over time but is depleted by consumption.
• If consumption exceeds regeneration, the resource may collapse, leading to population decline.
• Conversely, if the resource is abundant, the population may grow.

We will model this using the Lotka-Volterra equations, which are typically used for predator-prey dynamics but can also describe resource-consumer interactions.

Methodology

1. Population and Resource Dynamics:
   • Population growth is proportional to available resources.
   • Resource regeneration follows logistic growth.
2. Differential Equations:
   • dRdt=r⋅R(1−RK)−c⋅P⋅R
   • dPdt=e⋅c⋅P⋅R−m⋅P
     • R: Resource quantity
     • P: Population size
     • r: Resource growth rate
     • K: Carrying capacity of the resource
     • c: Consumption rate
     • e: Efficiency of resource to population growth
     • m: Mortality rate of the population
3. Simulation:
   • Use numerical integration to simulate population-resource dynamics over time.
4. Visualization:
   • Plot resource and population sizes over time.
   • Phase plot to observe cyclical behavior.

Required Libraries

We’ll use the following libraries:

• numpy: For numerical calculations.
• scipy: To solve differential equations.
• matplotlib: To visualize the results.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# Parameters
r = 0.5    # Resource growth rate
K = 100    # Resource carrying capacity
c = 0.02   # Consumption rate
e = 0.1    # Efficiency of resource use
m = 0.1    # Mortality rate of population

# Differential equations
def model(t, y):
    R, P = y
    dRdt = r * R * (1 - R / K) - c * P * R
    dPdt = e * c * P * R - m * P
    return [dRdt, dPdt]

# Initial conditions
R0 = 80   # Initial resource quantity
P0 = 10   # Initial population size
y0 = [R0, P0]

# Time span
t_span = (0, 200)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

# Solve differential equations
solution = solve_ivp(model, t_span, y0, t_eval=t_eval)

# Extract results
time = solution.t
R = solution.y[0]
P = solution.y[1]

# Plot Resource and Population over Time
plt.figure(figsize=(10, 5))
plt.plot(time, R, label='Resource', color='green')
plt.plot(time, P, label='Population', color='blue')
plt.title('Population and Resource Dynamics Over Time')
plt.xlabel('Time')
plt.ylabel('Quantity')
plt.legend()
plt.grid(True)
plt.show()

# Phase Plot (Resource vs Population)
plt.figure(figsize=(6, 6))
plt.plot(R, P, color='purple')
plt.title('Phase Plot: Resource vs Population')
plt.xlabel('Resource Quantity')
plt.ylabel('Population Size')
plt.grid(True)
plt.show()

Explanation

1. Differential Equations:
   • The resource grows logistically and is consumed by the population.
   • Population growth is dependent on resource availability.
2. Numerical Integration:
   We use scipy.integrate.solve_ivp() to numerically solve the differential equations over a specified time span.
3. Visualization:
   • Time Series Plot: Shows resource and population dynamics over time.
   • Phase Plot: Shows the relationship between resource and population size, revealing cyclical interactions.

Analysis of Results

1. Time Series Plot:
   

   • Oscillations in both resource and population sizes indicate cyclical predator-prey-like dynamics.
   • When the resource is abundant, the population grows.
   • As the population consumes the resource, the resource decreases, leading to a population decline.
   • This allows the resource to regenerate, starting the cycle again.

2. Phase Plot:
   

   • The cyclical pattern represents the feedback loop between resource availability and population growth.
   • The trajectory suggests a stable limit cycle, indicating sustainable oscillations rather than collapse or unbounded growth.

Environmental Implications

This model illustrates the delicate balance between resource consumption and population growth, relevant for:

• Sustainability Analysis: Ensuring renewable resources are not overexploited.
• Conservation Biology: Managing species populations and their habitats.
• Agricultural Planning: Balancing crop yields with environmental impacts.

Let’s consider a sociological example where we analyze the relationship between education level and income.

We’ll use Python to simulate data, analyze it, and visualize the results.

Example: Education Level and Income

Hypothesis: Higher education levels are associated with higher income.

Step 1: Simulate Data

We’ll create a synthetic dataset where:

• Education Level is measured in years (e.g., 12 years for high school, 16 for a bachelor’s degree, etc.).
• Income is measured in thousands of dollars per year.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# Set a seed for reproducibility
np.random.seed(42)

# Simulate data
n = 100  # Number of samples
education_level = np.random.randint(12, 21, n)  # Years of education (12 to 20 years)
income = 20 * education_level + np.random.normal(0, 10, n)  # Income in thousands of dollars

# Create a DataFrame
data = pd.DataFrame({'Education_Level': education_level, 'Income': income})

# Display the first few rows
print(data.head())

Step 2: Analyze the Data

We’ll use a simple linear regression to analyze the relationship between education level and income.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

from sklearn.linear_model import LinearRegression

# Prepare the data
X = data[['Education_Level']]
y = data['Income']

# Fit the model
model = LinearRegression()
model.fit(X, y)

# Get the coefficients
slope = model.coef_[0]
intercept = model.intercept_

print(f"Slope (Coefficient for Education Level): {slope}")
print(f"Intercept: {intercept}")

Step 3: Visualize the Results

We’ll plot the data points and the regression line to visualize the relationship.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# Plot the data points
plt.figure(figsize=(10, 6))
sns.scatterplot(x='Education_Level', y='Income', data=data, color='blue', label='Data Points')

# Plot the regression line
plt.plot(X, model.predict(X), color='red', label='Regression Line')

# Add labels and title
plt.xlabel('Education Level (Years)')
plt.ylabel('Income (Thousands of Dollars)')
plt.title('Relationship Between Education Level and Income')
plt.legend()

# Show the plot
plt.show()

Step 4: Interpret the Results

   Education_Level      Income
0               18  363.268452
1               15  299.188810
2               19  384.677948
3               16  327.361224
4               18  352.202981
Slope (Coefficient for Education Level): 19.71155398870412
Intercept: 5.404657619066882

• Slope (Coefficient for Education Level): This value indicates how much income increases for each additional year of education.

For example, if the slope is 20, it means that for each additional year of education, income increases by ＄20,000 on average.

• Intercept: This is the expected income when the education level is 0 years.
  In this context, it may not have a practical interpretation since education level cannot be 0.

Step 5: Conclusion

The scatter plot with the regression line shows a positive relationship between education level and income.

As education level increases, income tends to increase as well.

This supports our hypothesis that higher education levels are associated with higher income.

Full Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression

# Set a seed for reproducibility
np.random.seed(42)

# Simulate data
n = 100  # Number of samples
education_level = np.random.randint(12, 21, n)  # Years of education (12 to 20 years)
income = 20 * education_level + np.random.normal(0, 10, n)  # Income in thousands of dollars

# Create a DataFrame
data = pd.DataFrame({'Education_Level': education_level, 'Income': income})

# Display the first few rows
print(data.head())

# Prepare the data
X = data[['Education_Level']]
y = data['Income']

# Fit the model
model = LinearRegression()
model.fit(X, y)

# Get the coefficients
slope = model.coef_[0]
intercept = model.intercept_

print(f"Slope (Coefficient for Education Level): {slope}")
print(f"Intercept: {intercept}")

# Plot the data points
plt.figure(figsize=(10, 6))
sns.scatterplot(x='Education_Level', y='Income', data=data, color='blue', label='Data Points')

# Plot the regression line
plt.plot(X, model.predict(X), color='red', label='Regression Line')

# Add labels and title
plt.xlabel('Education Level (Years)')
plt.ylabel('Income (Thousands of Dollars)')
plt.title('Relationship Between Education Level and Income')
plt.legend()

# Show the plot
plt.show()

This code simulates data, fits a linear regression model, and visualizes the relationship between education level and income.

The results suggest that higher education levels are associated with higher income, which is a common finding in sociological research.

I’ll create a bioinformatics example that analyzes DNA sequences and visualizes the results.

We’ll create a program that:

1. Analyzes GC content across a DNA sequence using a sliding window
2. Finds potential CpG islands (regions with high GC content)
3. Visualizes the results

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

import numpy as np
import matplotlib.pyplot as plt

def calculate_gc_content(sequence, window_size=100, step_size=1):
    """
    Calculate GC content using a sliding window approach
    
    Args:
        sequence (str): DNA sequence
        window_size (int): Size of the sliding window
        step_size (int): Step size for sliding the window
        
    Returns:
        tuple: Positions and corresponding GC contents
    """
    positions = []
    gc_contents = []
    
    for i in range(0, len(sequence) - window_size + 1, step_size):
        window = sequence[i:i + window_size]
        gc_count = window.count('G') + window.count('C')
        gc_content = (gc_count / window_size) * 100
        positions.append(i)
        gc_contents.append(gc_content)
    
    return positions, gc_contents

def find_cpg_islands(positions, gc_contents, threshold=60):
    """
    Find potential CpG islands based on GC content threshold
    
    Args:
        positions (list): List of positions
        gc_contents (list): List of GC contents
        threshold (float): GC content threshold for CpG islands
        
    Returns:
        list: Start positions of potential CpG islands
    """
    islands = []
    for i, (pos, gc) in enumerate(zip(positions, gc_contents)):
        if gc > threshold:
            if not islands or pos - islands[-1] > 100:  # New island
                islands.append(pos)
    return islands

# Example DNA sequence (simulated)
np.random.seed(42)
bases = ['A', 'T', 'G', 'C']
sequence = ''.join(np.random.choice(bases, size=1000))

# Add a simulated CpG island
cpg_island = 'GC' * 50  # Create a GC-rich region
sequence = sequence[:400] + cpg_island + sequence[500:]

# Calculate GC content
positions, gc_contents = calculate_gc_content(sequence, window_size=100, step_size=10)

# Find CpG islands
cpg_islands = find_cpg_islands(positions, gc_contents)

# Plotting
plt.figure(figsize=(12, 6))
plt.plot(positions, gc_contents, 'b-', label='GC Content')
plt.axhline(y=60, color='r', linestyle='--', label='CpG Island Threshold')

# Mark CpG islands
for island in cpg_islands:
    plt.axvline(x=island, color='g', alpha=0.3)

plt.xlabel('Position in Sequence')
plt.ylabel('GC Content (%)')
plt.title('DNA Sequence Analysis: GC Content and CpG Islands')
plt.legend()
plt.grid(True)
plt.show()

# Print statistics
print(f"Average GC content: {np.mean(gc_contents):.2f}%")
print(f"Number of potential CpG islands: {len(cpg_islands)}")
for i, pos in enumerate(cpg_islands, 1):
    print(f"CpG island {i} starts at position {pos}")

Let me explain the code and its components:

1. Key Functions:

   • calculate_gc_content: Calculates GC content using a sliding window approach
   • find_cpg_islands: Identifies regions with high GC content (potential CpG islands)

2. Analysis Process:

   • We generate a random DNA sequence of 1000 bases
   • Insert a simulated CpG island (GC-rich region) in the middle
   • Calculate GC content using a 100bp window, sliding 10bp at a time
   • Identify regions where GC content exceeds 60% as potential CpG islands

3. Visualization:
   

   • Blue line shows GC content across the sequence
   • Red dashed line indicates the CpG island threshold (60%)
   • Green vertical lines mark the start of potential CpG islands
   • The plot includes proper labels and a legend

4. Statistics Output:

   Average GC content: 56.00%
   Number of potential CpG islands: 2
   CpG island 1 starts at position 300
   CpG island 2 starts at position 410
   

   • Calculates and displays average GC content
   • Shows the number and positions of potential CpG islands

This example demonstrates several important bioinformatics concepts:

• Sequence composition analysis
• Sliding window analysis
• Feature detection (CpG islands)
• Data visualization

I’ll create a historical data analysis example using Python.

Let’s analyze the rise and fall of different ancient civilizations by comparing their estimated population sizes over time.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# Create sample historical data
data = {
    'Year': [-3000, -2500, -2000, -1500, -1000, -500, 0],
    'Egyptian': [0.5, 1.5, 2.0, 3.0, 2.5, 2.0, 1.5],
    'Mesopotamian': [0.3, 2.0, 3.0, 2.5, 1.5, 1.0, 0.8],
    'Greek': [0.1, 0.2, 0.5, 1.0, 2.0, 3.5, 3.0],
    'Roman': [0.0, 0.1, 0.2, 0.5, 1.0, 2.5, 4.0]
}

# Create DataFrame
df = pd.DataFrame(data)

# Calculate total population and peak years for each civilization
analysis_results = {}
for civ in ['Egyptian', 'Mesopotamian', 'Greek', 'Roman']:
    peak_value = df[civ].max()
    peak_year = df.loc[df[civ].idxmax(), 'Year']
    analysis_results[civ] = {
        'Peak Population': peak_value,
        'Peak Year': peak_year
    }

# Create visualization
plt.figure(figsize=(12, 6))
for civ in ['Egyptian', 'Mesopotamian', 'Greek', 'Roman']:
    plt.plot(df['Year'], df[civ], marker='o', label=civ)

plt.title('Ancient Civilizations: Estimated Population Growth (Millions)')
plt.xlabel('Year (BCE/CE)')
plt.ylabel('Estimated Population (Millions)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()

# Add annotations for peak points
for civ in ['Egyptian', 'Mesopotamian', 'Greek', 'Roman']:
    peak_year = analysis_results[civ]['Peak Year']
    peak_pop = analysis_results[civ]['Peak Population']
    plt.annotate(f'{civ}\nPeak: {peak_pop}M',
                xy=(peak_year, peak_pop),
                xytext=(10, 10),
                textcoords='offset points')

print("Analysis Results:")
for civ, results in analysis_results.items():
    print(f"\n{civ}:")
    print(f"Peak Population: {results['Peak Population']} million")
    print(f"Peak Year: {results['Peak Year']} {'BCE' if results['Peak Year'] < 0 else 'CE'}")

Let me explain this historical data analysis:

1. Data Structure:

   • We created a dataset spanning from 3000 BCE to 0 CE
   • Tracked estimated populations (in millions) for four major ancient civilizations
   • Used simplified numbers for educational purposes

2. Analysis Features:

   • Tracks population changes over 3000 years
   • Identifies peak population periods for each civilization
   • Shows the transition of power between civilizations
   • Visualizes historical overlap between civilizations

3. Key Findings:

   • Egyptian civilization peaked earliest (around 1500 BCE)
   • Mesopotamian civilization peaked around 2000 BCE
   • Greek civilization reached its height around 500 BCE
   • Roman civilization was still rising at 0 CE
   • Shows clear patterns of civilizational succession

4. Visualization Features:
   

   • Line graph with distinct colors for each civilization
   • Markers showing specific data points
   • Grid lines for easier reading
   • Annotations showing peak points
   • Clear labels and legend

This code demonstrates several historical analysis concepts:

• Time series analysis of historical data
• Comparative analysis of concurrent civilizations
• Identification of peak periods and transitions
• Visualization of long-term historical trends

To explore a cosmology example using Python, we can calculate the Hubble parameter at different redshifts and visualize the results.

The Hubble parameter is crucial in cosmology as it describes the rate of expansion of the universe.

1. Theoretical Background

The Hubble parameter H(z) can be expressed as:

H(z)=H0√Ωm(1+z)3+ΩΛ

• H0 is the Hubble constant (approximately 70 km/s/Mpc).
• Ωm is the matter density parameter (approximately 0.3).
• ΩΛ is the dark energy density parameter (approximately 0.7).
• z is the redshift.

2. Python Code Implementation

Here’s how to implement this in Python:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import numpy as np
import matplotlib.pyplot as plt

# Constants
H0 = 70  # Hubble constant in km/s/Mpc
Omega_m = 0.3  # Matter density parameter
Omega_Lambda = 0.7  # Dark energy density parameter

# Function to calculate Hubble parameter
def hubble_parameter(z):
    return H0 * np.sqrt(Omega_m * (1 + z)**3 + Omega_Lambda)

# Redshift values
z_values = np.linspace(0, 3, 100)  # From 0 to 3
H_values = hubble_parameter(z_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(z_values, H_values, label='Hubble Parameter H(z)', color='blue')
plt.title('Hubble Parameter vs Redshift')
plt.xlabel('Redshift (z)')
plt.ylabel('Hubble Parameter (km/s/Mpc)')
plt.axhline(y=H0, color='r', linestyle='--', label='H0 = 70 km/s/Mpc')
plt.legend()
plt.grid()
plt.show()

3. Explanation of the Code

• Imports: We import numpy for numerical calculations and matplotlib.pyplot for plotting.

• Constants: We define the Hubble constant and density parameters.

• Function: The hubble_parameter function computes H(z) using the formula provided.

• Redshift Values: We create an array of redshift values ranging from 0 to 3.

• Calculation: We calculate the Hubble parameter for each redshift value.

• Plotting: We use matplotlib to create a plot of the Hubble parameter against redshift.
  A horizontal line indicates the Hubble constant value.

4. Result Interpretation

The graph shows how the Hubble parameter increases with redshift, indicating that the expansion rate of the universe was faster in the past.

The dashed red line represents the current value of the Hubble constant, providing a reference point.

This example illustrates a fundamental concept in cosmology and demonstrates how to use Python for calculations and visualizations in this field.

Example in Nuclear Physics

Problem Statement:

A radioactive substance undergoes exponential decay, which can be described by the equation:
N(t)=N0e−λt

• N(t) is the number of undecayed nuclei at time t.
• N0 is the initial number of nuclei.
• λ is the decay constant.
• t is time.

The half-life (T1/2) of the substance is related to λ by:
T1/2=ln(2)λ

Task:

1. Simulate radioactive decay for a sample of 1000 nuclei over 10 half-lives.
2. Plot the number of remaining nuclei as a function of time.
3. Verify that at T1/2, half of the original nuclei remain.

Python Implementation

Below is the Python code to solve and visualize the decay process.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt

# Constants
N0 = 1000  # Initial number of nuclei
half_life = 5  # Half-life in arbitrary time units
lambda_ = np.log(2) / half_life  # Decay constant

time = np.linspace(0, 10 * half_life, 1000)  # Time from 0 to 10 half-lives
N_t = N0 * np.exp(-lambda_ * time)  # Decay equation

# Plot results
plt.figure(figsize=(8, 5))
plt.plot(time, N_t, label=f"Radioactive Decay (Half-life = {half_life} units)", color='blue')
plt.axvline(half_life, linestyle='--', color='red', label=f"T_1/2 = {half_life} units")
plt.axhline(N0/2, linestyle='--', color='green', label=f"N = {N0//2} at T_1/2")

plt.xlabel("Time")
plt.ylabel("Remaining Nuclei")
plt.title("Exponential Radioactive Decay")
plt.legend()
plt.grid()
plt.show()

Explanation of the Code

1. Initialization:

   • The initial number of nuclei is set to 1000.
   • The half-life is defined as 5 arbitrary time units.
   • The decay constant λ is calculated using λ=ln(2)/T1/2.

2. Simulation:

   • Time is generated as an array from 0 to 10 half-lives.
   • The number of remaining nuclei is computed using the exponential decay formula.

3. Visualization:
   

   • A plot is generated showing the decay curve.
   • A vertical dashed line marks T1/2.
   • A horizontal dashed line marks N0/2, verifying that half of the nuclei remain at T1/2.

This provides a clear illustration of radioactive decay over time.

Let’s explore a problem in Chemistry related to chemical kinetics, specifically the rate of a first-order reaction.

A first-order reaction is one where the rate of reaction depends linearly on the concentration of a single reactant.

Problem Statement

We will model the concentration of a reactant over time for a first-order reaction and plot the concentration as a function of time.
The rate law for a first-order reaction is given by:
d[A]dt=−k[A]

• [A] = concentration of the reactant
• k = rate constant
• t = time

The integrated rate law for a first-order reaction is:
[A]=[A]0e−kt

• [A]0 = initial concentration of the reactant

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt

# Parameters
A0 = 1.0  # Initial concentration in mol/L
k = 0.1   # Rate constant in s^-1
time = np.linspace(0, 50, 500)  # Time range from 0 to 50 seconds

# Calculate concentration over time
A = A0 * np.exp(-k * time)

# Plot concentration vs time
plt.figure(figsize=(10, 6))
plt.plot(time, A, color='blue', linewidth=2, label='[A]')
plt.title('First-Order Reaction: Concentration vs Time')
plt.xlabel('Time (s)')
plt.ylabel('Concentration [A] (mol/L)')
plt.grid(True)

# Highlight half-life
half_life = np.log(2) / k
plt.axvline(x=half_life, color='red', linestyle='--', label=f'Half-life = {half_life:.2f} s')
plt.legend()
plt.show()

Explanation

1. Rate Law:

   • The rate of a first-order reaction is proportional to the concentration of the reactant:
     d[A]dt=−k[A]

2. Integrated Rate Law:

   • The integrated rate law for a first-order reaction is:
     [A]=[A]0e−kt
   • This equation describes how the concentration of the reactant decreases exponentially over time.

3. Parameters:

   • [A]0=1.0mol/L: Initial concentration of the reactant.
   • k=0.1s−1: Rate constant.

4. Time Range:

   • We define a time range from 0 to 50 seconds using np.linspace.

5. Plotting:

   • The concentration [A] is plotted as a function of time.
   • A vertical dashed line is added to highlight the half-life of the reaction.

Result

The graph shows the concentration of the reactant [A] as a function of time:

• At t=0, the concentration is [A]0=1.0,mol/L.
• As time increases, the concentration decreases exponentially.
• The half-life (t1/2) is the time required for the concentration to reduce to half of its initial value.
  For this reaction, the half-life is:
  t1/2=ln(2)k≈6.93s

Interpretation

• Exponential Decay: The concentration of the reactant decreases exponentially over time, which is characteristic of first-order kinetics.
• Half-Life: The half-life is constant for a first-order reaction and is independent of the initial concentration.
  This is a key feature of first-order reactions.

This example demonstrates how Python can be used to model and visualize chemical kinetics, providing insights into the behavior of chemical reactions.