Gamma Functions with SciPy

October 1, 2024

Gamma Functions with SciPy

The Gamma function is a generalization of the factorial function for real and complex numbers.

For a positive integer $( n )$, the Gamma function $( \Gamma(n) )$ is related to the factorial by the formula:

$$
\Gamma(n) = (n - 1)!
$$

For non-integer values, the Gamma function extends this definition, and is defined by the integral:

$$
\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt
$$

$SciPy$ provides support for the Gamma function and its variants through the scipy.special module.

Example Problem: Evaluating the Gamma Function

Problem Statement:

We want to compute the Gamma function for several values, including non-integer values, and plot it to visualize its behavior.
We will also calculate the Gamma function for fractional and large values using $SciPy$’s gamma function.

Steps to Solve:

Compute the Gamma Function for Integer Values: We will calculate $( \Gamma(n) )$ for positive integers and compare the results with factorial values.
Compute the Gamma Function for Non-Integer Values: We’ll also calculate it for some fractional values to see how it behaves.
Plot the Gamma Function: Visualize the Gamma function over a range of values to understand its shape and behavior.
Use SciPy’s gamma Function: Use the scipy.special.gamma function to evaluate the Gamma function at various points.

Implementation in Python:

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma

# Step 1: Compute the Gamma function for integer values
integer_values = np.array([1, 2, 3, 4, 5])
gamma_values_for_integers = gamma(integer_values)

# Step 2: Compute the Gamma function for non-integer values
fractional_values = np.array([0.5, 1.5, 2.5, 3.5])
gamma_values_for_fractionals = gamma(fractional_values)

# Print results for integer and fractional values
print("Gamma function values for integers:")
for n, g in zip(integer_values, gamma_values_for_integers):
    print(f"Gamma({n}) = {g:.4f}")

print("\nGamma function values for fractional values:")
for n, g in zip(fractional_values, gamma_values_for_fractionals):
    print(f"Gamma({n}) = {g:.4f}")

# Step 3: Plot the Gamma function for a range of values
x_values = np.linspace(0.1, 5, 100)  # Avoid zero to prevent singularity
y_values = gamma(x_values)

plt.plot(x_values, y_values, label="Gamma Function", color="blue")
plt.scatter(fractional_values, gamma_values_for_fractionals, color="red", label="Fractional Points")
plt.xlabel('x')
plt.ylabel('Gamma(x)')
plt.title('Gamma Function')
plt.legend()
plt.grid(True)
plt.show()

Explanation of the Code:

Gamma Function for Integer Values:
- The Gamma function for integers is calculated using the scipy.special.gamma function.
- For positive integers, the Gamma function is related to the factorial, so $( \Gamma(n) = (n - 1)! )$. For example, $( \Gamma(5) = 4! = 24 )$.
Gamma Function for Fractional Values:
- The Gamma function can also be evaluated for non-integer values.
  For example, $( \Gamma(0.5) )$ is a well-known value related to the square root of $( \pi )$, and $( \Gamma(1.5) )$ is another commonly used value.
Visualization:
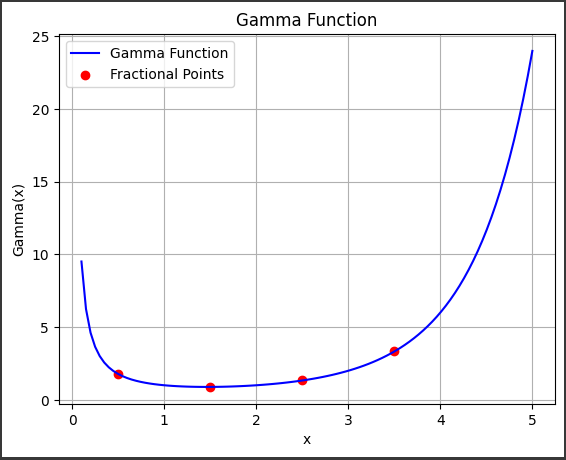
- The Gamma function is plotted for a range of values between $0.1$ and $5$ (avoiding zero, where the Gamma function has a singularity).
- Fractional values are highlighted as red dots on the plot, showing their specific values on the curve.
Output:
- The results for the Gamma function at integer and fractional values are printed and visualized on the plot.

Output:

Gamma function values for integers:
Gamma(1) = 1.0000
Gamma(2) = 1.0000
Gamma(3) = 2.0000
Gamma(4) = 6.0000
Gamma(5) = 24.0000

Gamma function values for fractional values:
Gamma(0.5) = 1.7725
Gamma(1.5) = 0.8862
Gamma(2.5) = 1.3293
Gamma(3.5) = 3.3234

Interpretation of Results:

Gamma Function for Integers:
- As expected, the Gamma function for integer values $( \Gamma(n) )$ returns $( (n - 1)! )$. For example, $( \Gamma(5) = 24 )$, which is the factorial of $4$.
Gamma Function for Non-Integer Values:
- The Gamma function returns meaningful values for non-integer inputs. For example, $( \Gamma(0.5) = 1.7725 )$, which is $( \sqrt{\pi} )$, and $( \Gamma(1.5) = 0.8862 )$, showing the smooth continuation of the factorial function to fractional values.

Visualization:

The plot of the Gamma function shows a curve that increases as $( x )$ increases, except for fractional values where the function smoothly interpolates between factorials.
Fractional values like $( 0.5 )$ and $( 1.5 )$ are marked on the plot to show where these values lie on the curve.

Key Concepts:

Gamma Function:
- The Gamma function is a continuous extension of the factorial function to real and complex numbers. For non-integer values, it can be computed via the integral definition.
gamma Function in SciPy:
- $SciPy$’s gamma function efficiently computes the Gamma function for both real and complex numbers, making it useful in various fields such as statistics, physics, and engineering.
Relation to Factorial:
- For integer values $( n )$, $( \Gamma(n) = (n - 1)! )$, linking the Gamma function to the factorial.
Special Values:
- $( \Gamma(0.5) = \sqrt{\pi} \approx 1.7725 )$ is a frequently used value in probability and statistics.

Conclusion:

This example demonstrates how to calculate the Gamma function for both integer and non-integer values using $SciPy$.

The function generalizes the concept of the factorial, providing meaningful values for non-integer arguments.

We also visualized the Gamma function over a range of values, showing how it smoothly interpolates between the factorial values.

The scipy.special.gamma function is an essential tool for solving problems involving continuous extensions of the factorial, especially in fields like mathematics and engineering.

Optimization Problems with SciPy

September 30, 2024

Optimization Problems with SciPy

Optimization problems involve finding the minimum or maximum of a function, subject to constraints (if any).

$SciPy$ provides a variety of optimization algorithms through the scipy.optimize module.

The most common problem is to find the minimum of a scalar function, often referred to as unconstrained optimization.

Example Problem: Minimizing a Nonlinear Function

Problem Statement:

Suppose we want to minimize the following nonlinear function:

$$
f(x, y) = (x - 2)^2 + (y - 3)^2 + \sin(x) \cdot \cos(y)
$$

This is a two-variable function that includes both quadratic terms and trigonometric components.

The goal is to find the values of $( x )$ and $( y )$ that minimize $( f(x, y) )$.

Steps to Solve:

Define the Objective Function: We need to define the function $( f(x, y) $) in $Python$.
Use SciPy’s minimize Function: $SciPy$’s minimize function can be used to find the minimum of a multivariable function.
Provide an Initial Guess: The optimization algorithm needs an initial guess for $( x )$ and $( y )$ from where it will start searching for the minimum.
Analyze the Results: We’ll check the values of $( x )$ and $( y )$ that minimize the function.

Implementation in Python:

import numpy as np
from scipy.optimize import minimize

# Step 1: Define the objective function
def objective_function(variables):
    x, y = variables
    return (x - 2)**2 + (y - 3)**2 + np.sin(x) * np.cos(y)

# Step 2: Provide an initial guess for x and y
initial_guess = [0, 0]  # Starting point for the optimization

# Step 3: Perform the optimization using 'minimize'
result = minimize(objective_function, initial_guess)

# Extract the optimized values of x and y
x_opt, y_opt = result.x
minimum_value = result.fun

# Step 4: Display the results
print(f"Optimal values: x = {x_opt:.4f}, y = {y_opt:.4f}")
print(f"Minimum value of the function: f(x, y) = {minimum_value:.4f}")

Explanation of the Code:

Defining the Objective Function:
- The function $( f(x, y) = (x - 2)^2 + (y - 3)^2 + \sin(x) \cdot \cos(y) )$ is defined using $Python$’s $NumPy$ library for mathematical operations.
- This function represents the objective we want to minimize.
  The quadratic terms $((x - 2)^2)$ and $((y - 3)^2)$ will pull $(x)$ towards $2$ and $(y)$ towards $3$, while the sinusoidal part adds complexity to the surface of the function.
Initial Guess:
- The optimization algorithm needs a starting point.
  In this case, we choose an initial guess of $(x = 0)$ and $(y = 0)$.
- The algorithm will use this point to begin searching for the minimum of the function.
Minimizing the Function:
- We use the minimize function from scipy.optimize, which applies a general-purpose optimization algorithm (by default, it uses the BFGS algorithm, which is gradient-based).
- The result of minimize contains several important details, such as the optimized values of $( x )$ and $( y )$, and the minimum value of the function.
Output:
- The optimized values of $( x )$ and $( y )$ are printed, along with the corresponding minimum value of the function.

Output:

1 2	Optimal values: x = 1.8587, y = 3.0458 Minimum value of the function: f(x, y) = -0.9324

Analysis of the Results:

The function achieves its minimum at approximately $( x = 1.8587 )$ and $( y = 3.0458 )$.
The minimum value of the function at this point is $( f(x, y) = -0.9324 )$.

Visualization (Optional):

We can visualize the surface of the function $( f(x, y) )$ to better understand where the minimum occurs.

Here’s how you can plot the function and highlight the minimum point:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Create a grid of points for x and y
x_vals = np.linspace(-1, 4, 100)
y_vals = np.linspace(0, 6, 100)
X, Y = np.meshgrid(x_vals, y_vals)

# Compute the function values at each grid point
Z = (X - 2)**2 + (Y - 3)**2 + np.sin(X) * np.cos(Y)

# Plot the surface of the function
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none', alpha=0.8)

# Mark the optimal point
ax.scatter(x_opt, y_opt, minimum_value, color='r', s=100, label="Minimum")

# Add labels and title
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
ax.set_title('Surface of the Objective Function')
plt.legend()
plt.show()

Output:

Key Concepts:

Objective Function: This is the function we are trying to minimize.
In this example, the objective function is nonlinear and consists of both quadratic and sinusoidal terms.
minimize Function: This function in $SciPy$ is a general-purpose optimizer for minimizing scalar functions of one or more variables.
It supports various methods, such as:
- BFGS: A quasi-Newton method (used by default) that is efficient for smooth, continuous functions.
- Nelder-Mead: A derivative-free simplex algorithm, useful for nonsmooth functions.
Initial Guess: The optimization process starts from an initial guess, and different guesses may lead to different solutions, especially for nonlinear functions with multiple local minima.
Global vs. Local Minima: For complex functions, the minimize function may find a local minimum instead of the global minimum, depending on the starting point and the shape of the function.

Conclusion:

This example demonstrates how to use $SciPy$’s minimize function to solve an optimization problem involving a nonlinear function.

The function is minimized by adjusting the variables $( x )$ and $( y )$, and the algorithm efficiently finds the point where the function reaches its lowest value.

This process is fundamental in many fields, including machine learning, economics, and engineering, where optimization problems arise frequently.

Nonlinear Least Squares Curve Fitting with SciPy

September 29, 2024

Nonlinear Least Squares Curve Fitting with SciPy

Nonlinear least squares curve fitting is a process where we fit a nonlinear model to a set of data points by minimizing the sum of the squares of the residuals (the differences between observed and model-predicted values).

$SciPy$ provides the curve_fit function in scipy.optimize to perform this fitting.

Example Problem: Fitting an Exponential Decay Model

Problem Statement:

We have some experimental data that is expected to follow an exponential decay function of the form:

$$
y = a \cdot e^{-b \cdot x} + c
$$

Where:

$( a )$, $( b )$, and $( c )$ are the parameters to be estimated.
$( x )$ is the independent variable (e.g., time).
$( y )$ is the observed dependent variable (e.g., concentration, temperature, etc.).

Given a set of noisy data points generated by the above equation, we will use nonlinear least squares fitting to estimate the values of $( a )$, $( b )$, and $( c )$.

Steps to Solve:

Generate Noisy Data: Create synthetic data based on the exponential decay function and add some noise to simulate real-world experimental data.
Define the Model Function: Create a $Python$ function for the exponential decay model.
Use curve_fit to Estimate Parameters: Fit the model to the data using $SciPy$’s curve_fit.
Plot the Results: Compare the original noisy data with the fitted curve.

Implementation in Python:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# Step 1: Generate synthetic data
np.random.seed(0)  # For reproducibility
x_data = np.linspace(0, 4, 50)  # Independent variable (e.g., time)
# True parameters for generating the data
a_true, b_true, c_true = 2.5, 1.3, 0.5
# Generate noisy data based on the exponential decay model
y_data = a_true * np.exp(-b_true * x_data) + c_true + 0.2 * np.random.normal(size=len(x_data))

# Step 2: Define the model function (Exponential Decay)
def model_func(x, a, b, c):
    return a * np.exp(-b * x) + c

# Step 3: Perform curve fitting to estimate the parameters
initial_guess = [2, 1, 0]  # Initial guess for the parameters (a, b, c)
params, covariance = curve_fit(model_func, x_data, y_data, p0=initial_guess)

# Extract the fitted parameters
a_fit, b_fit, c_fit = params

# Step 4: Generate the fitted curve
y_fit = model_func(x_data, *params)

# Display the fitted parameters
print(f"Fitted Parameters: a = {a_fit:.3f}, b = {b_fit:.3f}, c = {c_fit:.3f}")

# Step 5: Plot the original data and the fitted curve
plt.scatter(x_data, y_data, label="Noisy Data", color="blue")
plt.plot(x_data, y_fit, label=f"Fitted Curve: $y = {a_fit:.2f}e^{{-{b_fit:.2f}x}} + {c_fit:.2f}$", color="red")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Nonlinear Least Squares Curve Fitting: Exponential Decay")
plt.legend()
plt.grid(True)
plt.show()

Explanation of the Code:

Synthetic Data Generation:
- We generate the independent variable $( x )$ as $50$ equally spaced points between $0$ and $4$.
- We generate noisy data for $( y )$ using the exponential decay function with true parameters $( a = 2.5 )$, $( b = 1.3 )$, and $( c = 0.5 )$.
  We add random $Gaussian$ $noise$ with a standard deviation of $0.2$ to simulate real-world measurement noise.
Model Function:
- We define the model function model_func(x, a, b, c), which represents the exponential decay function we are trying to fit to the data.
Curve Fitting:
- The curve_fit function takes the model function, the independent variable $( x )$, and the noisy observed data $( y )$, and attempts to find the parameters $( a )$, $( b )$, and $( c )$ that best fit the data.
- We provide an initial guess for the parameters.
  The algorithm iterates to minimize the sum of squared residuals and returns the best-fit parameters.
Fitted Curve:
- We use the estimated parameters to compute the fitted curve and compare it against the noisy data.
Plotting:
- We plot the noisy data points and the fitted curve on the same graph to visualize how well the model fits the data.

Output:

Plot:

The plot will show the noisy data points (in blue) and the fitted exponential decay curve (in red).
The fitted curve should align well with the noisy data, demonstrating that the curve-fitting process has accurately captured the underlying trend despite the noise.

Interpretation:

The fitted parameters $( a )$, $( b )$, and $( c )$ are very close to the true values used to generate the data:
- True values: $( a = 2.5 )$, $( b = 1.3 )$, $( c = 0.5 )$
- Fitted values: $( a = 2.807 )$, $( b = 1.246 )$, $( c = 0.445 )$
The slight differences between the true and fitted values are due to the noise added to the data, which is common in real-world experiments.

Key Concepts:

Nonlinear Least Squares: A method for fitting a nonlinear model to data by minimizing the sum of the squared differences between the observed and predicted values.
curve_fit Function: This function in $SciPy$ is designed to perform nonlinear least squares fitting.
It is a versatile tool that can handle a wide range of models.
Covariance Matrix: curve_fit also returns a covariance matrix, which can be used to estimate the uncertainty in the fitted parameters.
This is particularly useful in statistical modeling when you need to quantify the confidence in the parameter estimates.

This example demonstrates how to use nonlinear least squares curve fitting to fit an exponential decay model to noisy data.

Numerical Integration Example with SciPy

September 28, 2024

Numerical Integration Example with SciPy

Numerical integration is the process of finding the approximate value of an integral when it cannot be computed analytically.

In $SciPy$, the quad function from the scipy.integrate module is commonly used for this purpose.

It uses adaptive quadrature methods to calculate definite integrals efficiently.

Example Problem: Integrating a Function

Problem Statement:

We want to compute the integral of the following function over a specific interval:

$$
f(x) = e^{-x^2}
$$

We are asked to calculate the definite integral of this function from $(x = 0)$ to $(x = 1)$:

$$
I = \int_0^1 e^{-x^2} , dx
$$

This is a Gaussian-like function, and its integral does not have a simple analytical solution, so we will use numerical methods to compute it.

Solution Approach:

Define the Function: Create a $Python$ function for $(f(x) = e^{-x^2})$.
Use SciPy’s quad Function: This function computes the integral using an adaptive quadrature method.
Display the Result: We will compute the value of the integral and display it along with the estimated error.

Implementation in Python:

import numpy as np
from scipy.integrate import quad

# Step 1: Define the function to be integrated
def integrand(x):
    return np.exp(-x**2)

# Step 2: Perform the numerical integration from 0 to 1 using quad
result, error = quad(integrand, 0, 1)

# Display the result and the estimated error
print(f"Integral of exp(-x^2) from 0 to 1: {result}")
print(f"Estimated error in the computation: {error}")

Explanation:

Defining the Function:
- The function we are integrating is $(f(x) = e^{-x^2})$, a rapidly decaying Gaussian-like function.
- We define this function in $Python$ using $NumPy$’s exp function to handle the exponential.
Using quad for Numerical Integration:
- $SciPy$’s quad function is used for computing the definite integral. The quad function returns two values:
  - The result of the integration (the estimated value of the integral).
  - The error estimate, which tells us how accurate the numerical approximation is.
- The function takes three arguments: the integrand (function to be integrated), the lower bound $(0)$, and the upper bound $(1)$ of the integral.
Result and Error:
- The result is the approximate value of the definite integral, and the error estimate gives an indication of how close the approximation is to the actual value. In most cases, the error will be very small.

Output:

1 2	Integral of exp(-x^2) from 0 to 1: 0.7468241328124271 Estimated error in the computation: 8.291413475940725e-15

Analysis of the Result:

The integral of $(e^{-x^2})$ from $0$ to $1$ is approximately 0.7468.
The estimated error in the computation is extremely small, about $(8.29 \times 10^{-15})$, which indicates that the result is very accurate.

Visualization (Optional):

We can visualize the function $(e^{-x^2})$ and the area under the curve from $(x = 0)$ to $(x = 1)$ to better understand what the integral represents.

import matplotlib.pyplot as plt

# Create an array of x values from 0 to 1
x_values = np.linspace(0, 1, 500)
y_values = integrand(x_values)

# Plot the function
plt.plot(x_values, y_values, label=r'$e^{-x^2}$', color='blue')

# Fill the area under the curve from 0 to 1
plt.fill_between(x_values, y_values, alpha=0.2, color='blue')

# Add labels and title
plt.title('Numerical Integration of $e^{-x^2}$ from 0 to 1')
plt.xlabel('x')
plt.ylabel(r'$e^{-x^2}$')
plt.grid(True)
plt.legend()

# Show the plot
plt.show()

Key Takeaways:

Numerical Integration: A method used to approximate the value of definite integrals when an exact analytical solution is difficult or impossible to obtain.
SciPy’s quad function: A powerful tool for performing numerical integration, capable of handling a wide variety of functions with high accuracy.
Error Estimation: quad also provides an estimate of the error in the approximation, helping to ensure the reliability of the result.

This example demonstrates how to use $SciPy$ to compute a definite integral numerically and shows how the integral of the function $(e^{-x^2})$ is approximated over a specific range.

Interpolation Example with SciPy

September 27, 2024

Interpolation Example with SciPy

Interpolation is the process of estimating unknown values that fall between known data points.

It is widely used in data analysis, numerical simulations, and scientific computing.

$SciPy$ provides a variety of interpolation methods to make this process easy and efficient.

Example Problem: Linear Interpolation

Problem Statement:

Suppose you have the following data points representing some measurements:

$$
x = [0, 1, 2, 3, 4, 5]
$$
$$
y = [0, 0.8, 0.9, 0.1, -0.8, -1.0]
$$

You want to interpolate the value of $(y)$ at intermediate points $(x = 2.5)$, $(x = 3.5)$, and also create a smooth curve for $(x)$ values between $0$ and $5$.

Solution Approach:

Use SciPy’s interp1d function:
This function performs $1D$ interpolation and allows you to estimate values between known data points.
Choose Linear Interpolation:
We’ll start with simple linear interpolation to estimate the values at specific points and also generate a smooth curve.
Visualize the Results:
We’ll plot both the original data points and the interpolated values to see how well the interpolation works.

Implementation in Python:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

# Step 1: Define the known data points
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 0.8, 0.9, 0.1, -0.8, -1.0])

# Step 2: Create an interpolation function using linear interpolation
linear_interp = interp1d(x, y, kind='linear')

# Step 3: Interpolate values at intermediate points
x_new = np.array([2.5, 3.5])
y_new = linear_interp(x_new)

# Step 4: Generate a smooth curve for plotting
x_smooth = np.linspace(0, 5, 100)
y_smooth = linear_interp(x_smooth)

# Display the interpolated values
print("Interpolated values at x = 2.5 and x = 3.5:")
print(y_new)

# Step 5: Plot the original data points, the interpolated points, and the smooth curve
plt.plot(x, y, 'o', label='Original Data', color='blue')  # Original data points
plt.plot(x_smooth, y_smooth, '-', label='Interpolated Curve', color='green')  # Interpolated curve
plt.plot(x_new, y_new, 'x', label='Interpolated Points', color='red')  # Interpolated points

# Add labels and legend
plt.title("Linear Interpolation with SciPy")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()

# Show the plot
plt.grid(True)
plt.show()

Explanation:

Data Points:
- The given data points $(x = [0, 1, 2, 3, 4, 5])$ represent the independent variable, and $(y = [0, 0.8, 0.9, 0.1, -0.8, -1.0])$ represent the dependent variable.
- These data points may represent measurements or observations at specific intervals.
Linear Interpolation:
- We use $SciPy$’s interp1d function with the argument kind='linear', which fits a straight line between each pair of adjacent data points.
- This function returns an interpolation object that can be used to estimate $(y)$ values for any intermediate $(x)$ values within the range of the given data.
Interpolating Specific Points:
- We estimate the value of $(y)$ at $(x = 2.5)$ and $(x = 3.5)$. The interpolation function gives approximate values at these points by calculating the linear relationship between the adjacent known data points.
Creating a Smooth Curve:
- To better visualize the interpolation, we generate a smooth curve by evaluating the interpolation function for $100$ evenly spaced $(x)$ values between $0$ and $5$.
  This helps us see how the interpolated function behaves across the entire range.
Visualization:
- We plot the original data points (blue circles), the interpolated points (red crosses), and the interpolated curve (green line).
- This allows us to visually confirm that the interpolated points lie on the line formed by connecting the original data points.

Output:

This output shows that the value of $(y)$ at $(x = 2.5)$ is approximately $0.5$ and at $(x = 3.5)$ is approximately $-0.35$.

Key Takeaways:

Interpolation is a useful tool when you have discrete data points and need to estimate values between them.
Linear interpolation connects data points with straight lines, providing a simple way to estimate values between known points.
SciPy’s interp1d function allows for easy implementation of various interpolation methods, including linear, cubic, and spline interpolation.

This example demonstrates how to perform linear interpolation using $SciPy$ and visualize the results with a plot.

Bessel Functions Example with SciPy

September 26, 2024

Bessel Functions Example with SciPy

Bessel functions, often denoted as $(J_n(x))$, are solutions to Bessel’s differential equation and are widely used in solving problems in physics, engineering, and applied mathematics, especially when dealing with cylindrical or spherical symmetry.

The Bessel function of the first kind, $(J_n(x))$, is defined as the solution to the differential equation:

$$
x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - n^2)y = 0
$$

where $(n)$ is the order of the Bessel function, and $(x)$ is the argument.
$SciPy$ provides efficient implementations of Bessel functions.

Example Problem: Compute the Bessel Function of the First Kind

Problem Statement:

Compute the values of the Bessel function of the first kind $(J_n(x))$ for different orders $(n)$ and arguments $(x)$.
Specifically, calculate $(J_0(x))$, $(J_1(x))$, and $(J_2(x))$ for $(x)$ in the range from $0$ to $10$.

Solution Approach:

Use SciPy’s scipy.special.jn Function: $SciPy$ has a built-in jn(n, x) function to compute the Bessel function of the first kind for a given order $(n)$ and argument $(x)$.
Plot the Results: We’ll visualize the Bessel functions to understand their behavior for different orders.

Implementation in Python:

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jn

# Step 1: Define the x values (from 0 to 10)
x = np.linspace(0, 10, 100)

# Step 2: Compute Bessel functions of different orders
J0 = jn(0, x)  # Bessel function of order 0
J1 = jn(1, x)  # Bessel function of order 1
J2 = jn(2, x)  # Bessel function of order 2

# Step 3: Plot the Bessel functions
plt.plot(x, J0, label='J_0(x)', color='blue')
plt.plot(x, J1, label='J_1(x)', color='red')
plt.plot(x, J2, label='J_2(x)', color='green')

# Add labels and legend
plt.title("Bessel Functions of the First Kind")
plt.xlabel("x")
plt.ylabel("J_n(x)")
plt.legend()

# Show the plot
plt.grid(True)
plt.show()

Explanation:

Compute Bessel Functions:
- We use jn(n, x) to compute the Bessel functions of the first kind for orders $(n = 0)$, $(n = 1)$, and $(n = 2)$.
  The function takes two arguments: the order $(n)$ and the value $(x)$, for which the Bessel function is to be evaluated.
Plot the Results:
- We plot the Bessel functions $(J_0(x))$, $(J_1(x))$, and $(J_2(x))$ over the interval $(x = [0, 10])$ to visualize their behavior.
Bessel functions oscillate and decay as $(x)$ increases.
Visualization:
- The plot shows how the functions $(J_0(x))$, $(J_1(x))$, and $(J_2(x))$ behave, each having a distinct pattern of oscillation, with their amplitudes gradually decreasing as $(x)$ grows larger.

Key Takeaways:

Bessel functions are important in many physical problems involving wave propagation, heat conduction, and vibrations in cylindrical or spherical geometries.
$SciPy$ provides the jn function to easily compute the Bessel function of the first kind for any given order $(n)$ and argument $(x)$.
The oscillating nature of Bessel functions is particularly useful in modeling real-world wave phenomena.

This example demonstrates how to compute and visualize Bessel functions using $SciPy$ and how they behave for different orders.

Result

This graph illustrates the Bessel functions of the first kind, specifically $(J_0(x))$, $(J_1(x))$, and $(J_2(x))$, over the interval from $(x = 0)$ to $(x = 10)$.

Blue Line: Represents $(J_0(x))$, the zeroth-order Bessel function.
It starts from approximately $1$ at $(x = 0)$ and oscillates with decreasing amplitude as $(x)$ increases.
This function crosses the $x$-$axis$ at several points, indicating the roots of $(J_0(x))$.
Red Line: Represents $(J_1(x))$, the first-order Bessel function.
It starts from $0$ at $(x = 0)$ and oscillates similarly to $(J_0(x))$ but with a slight phase shift.
The peaks and troughs are also diminishing in amplitude as $(x)$ increases.
Green Line: Represents $(J_2(x))$, the second-order Bessel function.
It also begins close to $0$, showing similar oscillatory behavior but with its own distinct peaks and troughs, spaced differently from $(J_0(x))$ and $(J_1(x))$.

Overall, the graph shows how each Bessel function of different orders behaves as a function of $(x)$, highlighting their oscillatory nature which is critical in applications involving cylindrical or spherical symmetry in physical problems.

Linear Algebra Example with SciPy

September 25, 2024

Linear Algebra Example with SciPy

Linear Algebra is a branch of mathematics that deals with vectors, matrices, and systems of linear equations.

It is fundamental in many fields, including engineering, physics, computer science, and economics.

$SciPy$ provides robust tools for performing a wide range of linear algebra operations efficiently.

Example Problem: Solving a System of Linear Equations

Problem Statement:

Consider the following system of linear equations:

$$
3x + 4y + 2z = 25
$$
$$
2x + y + 3z = 15
$$
$$
x + 2y + z = 10
$$

We need to solve this system to find the values of $(x)$, $(y)$, and $(z)$.

Solution Approach:

Matrix Representation: Represent the equations in matrix form $(A \cdot \mathbf{x} = \mathbf{b})$, where:
- $(A)$ is the coefficient matrix.
- $(\mathbf{x})$ is the vector of unknowns $([x, y, z])$.
- $(\mathbf{b})$ is the right-hand side vector.
Solve Using SciPy: Use $SciPy$’s solve function from the scipy.linalg module to find the solution vector $(\mathbf{x})$.

Implementation in Python:

import numpy as np
from scipy.linalg import solve

# Step 1: Define the coefficient matrix A
A = np.array([[3, 4, 2],
              [2, 1, 3],
              [1, 2, 1]])

# Step 2: Define the right-hand side vector b
b = np.array([25, 15, 10])

# Step 3: Solve the linear system A * x = b
x = solve(A, b)

# Display the solution
print("Solution vector x:")
print(x)

Explanation:

Matrix Representation:
- The coefficient matrix $( A )$ contains the coefficients of the variables $(x)$, $(y)$, and $(z)$.
- The vector $( \mathbf{b} )$ contains the constants on the right side of the equations.
Using solve Function:
- The solve function computes the solution of the linear system using efficient algorithms (like LU decomposition).
- The solution vector $(\mathbf{x})$ contains the values of $(x)$, $(y)$, and $(z)$ that satisfy the equations.
Output:
- The code will print the solution vector, giving the specific values for $(x)$, $(y)$, and $(z)$.

1 2	Solution vector x: [5. 2. 1.]

Advantages of Using SciPy for Linear Algebra:

Efficiency: $SciPy$’s linear algebra functions are optimized for performance and handle large-scale systems well.
Ease of Use: Simple syntax allows for straightforward implementation of complex linear algebra operations.
Robustness: $SciPy$’s functions are built on highly reliable numerical libraries, ensuring accurate results.

This example showcases how to use $SciPy$ to solve a typical system of linear equations, demonstrating the power and simplicity of its linear algebra tools.

Sparse Matrices Example with SciPy

September 24, 2024

Sparse Matrices Example with SciPy

Sparse matrices are matrices that contain a large number of zero elements.

In many scientific and engineering applications, sparse matrices are used to save memory and computational resources.

$SciPy$ provides various tools to work with sparse matrices efficiently, allowing for storage, manipulation, and solving of linear systems.

Example Problem: Solving a Linear System with Sparse Matrices

Problem Statement:

Consider a system of linear equations represented by a sparse matrix:

Our goal is to solve for the vector $(\mathbf{x})$ using $SciPy$’s sparse matrix functionalities.

Solution Approach:

Create the Sparse Matrix: We will use the csr_matrix (Compressed Sparse Row) format from $SciPy$ to represent the matrix.
This format is efficient for matrix-vector multiplication and other operations.
Set up the Equation: Define the matrix $(A)$ and the vector $(b)$.
Solve the Linear System: Use the spsolve function from $SciPy$, which is specifically designed to solve sparse linear systems.

Implementation in Python:

import numpy as np
from scipy.sparse import csr_matrix
from scipy.sparse.linalg import spsolve

# Step 1: Define the sparse matrix A
data = [4, 1, 3, 1, 5, 2, 2, 4]        # Non-zero values
rows = [0, 0, 1, 2, 2, 2, 3, 3]        # Row indices of non-zero values
cols = [0, 2, 1, 0, 2, 3, 2, 3]        # Column indices of non-zero values

# Create the sparse matrix in CSR format
A = csr_matrix((data, (rows, cols)), shape=(4, 4))

# Step 2: Define the right-hand side vector b
b = np.array([7, 3, 14, 8])

# Step 3: Solve the linear system A * x = b
x = spsolve(A, b)

# Display the solution
print("Solution vector x:")
print(x)

Explanation:

Matrix Representation: We use csr_matrix to create a sparse representation of matrix $( A )$.
The data array contains non-zero values, while rows and cols arrays specify their positions.
Solving the System: The spsolve function solves the sparse linear system efficiently, using LU decomposition under the hood, optimized for sparse matrix operations.
Output: The code outputs the solution vector $( \mathbf{x} )$.

Advantages of Using Sparse Matrices:

Memory Efficiency: Sparse matrices only store non-zero values, saving significant memory.
Computational Efficiency: Operations on sparse matrices are faster due to optimized storage schemes.
Scalability: Sparse matrices allow working with large-scale problems that would otherwise be infeasible with dense matrices.

Expected Output

1 2	Solution vector x: [1.2 1. 2.2 0.9]

The solution vector $(\mathbf{x} = [1.2, 1.0, 2.2, 0.9])$ represents the values of the variables $(x_1)$, $(x_2)$, $(x_3)$, and $(x_4)$ that satisfy the system of linear equations defined by the sparse matrix.

This means that when these values are substituted into the original equations, they balance the system, effectively solving $(A \times \mathbf{x} = \mathbf{b})$.

In simple terms, these values are the answers that make the equations true.

This example demonstrates how to effectively use $SciPy$’s sparse matrix tools to handle and solve linear systems, highlighting the benefits of sparse data structures in numerical computing.

Root Finding with SciPy： Solving Nonlinear Equations

September 23, 2024

Root Finding with SciPy： Solving Nonlinear Equations

Here’s an example of a root-finding problem solved using $SciPy$.

We will find the root of a nonlinear equation using the scipy.optimize module.

Scenario: Suppose you need to find the root of the following nonlinear equation, which is common in physics, engineering, or financial modeling:

$$
f(x) = x^3 - 4x^2 + 6x - 24 = 0
$$

Our goal is to find the value of $( x )$ where the function $( f(x) )$ equals zero.
This means we are looking for the root of the equation.

Solution Approach

To solve this problem, we will use $SciPy$’s fsolve() function, which is designed to find the roots of a given function.
fsolve() uses numerical methods to approximate the root and is highly effective for complex equations where analytical solutions are difficult or impossible.

Step-by-Step Solution Using SciPy

Define the Function: Define the equation $( f(x) = x^3 - 4x^2 + 6x - 24 )$.
Use fsolve() from SciPy: Use the fsolve() function to find the root, providing an initial guess close to where we expect the root to be.
Interpret the Results: The function will return the root value, which can then be interpreted as the solution to the equation.

Here’s the implementation in Python:

import numpy as np
from scipy.optimize import fsolve

# Define the nonlinear function
def equation(x):
    return x**3 - 4*x**2 + 6*x - 24

# Initial guess for the root
initial_guess = 5

# Use fsolve to find the root
root = fsolve(equation, initial_guess)

# Print the results
print(f"Root found: x = {root[0]:.4f}")

# Verify the result by substituting back into the original equation
verification = equation(root[0])
print(f"Verification (should be close to 0): f({root[0]:.4f}) = {verification:.4e}")

Explanation of the Code

Function Definition:
The function equation(x) represents the nonlinear equation we want to solve.
Initial Guess:
The initial_guess value is an estimate of where the root might be. This helps fsolve() start its search.
Different initial guesses can lead to different roots, especially if the function has multiple roots.
Finding the Root:
fsolve(equation, initial_guess) finds the root of the function starting from the initial guess.
It returns an array with the root value.
Verification:
To ensure the root is accurate, we substitute the root back into the equation to see if the result is approximately zero.

Expected Output

1 2	Root found: x = 4.0000 Verification (should be close to 0): f(4.0000) = 0.0000e+00

Interpretation of the Output

The output indicates that the root of the equation was found at $( x = 4.0000 )$.
This means that when $( x = 4.0000 )$, the function $( f(x) = x^3 - 4x^2 + 6x - 24 )$ equals zero, confirming that this is indeed a root of the equation.

The verification step shows that substituting $( x = 4.0000 )$ into the function results in a value of $( 0.0000e+00 )$, which is exactly zero, as expected.
This confirms that the solution is accurate and the root has been correctly identified.

In summary, $( x = 4.0000 )$ is a precise root of the given equation, and the verification confirms the correctness of the result.

Conclusion

$SciPy$’s fsolve() function provides a powerful way to find the roots of nonlinear equations, which are prevalent in various scientific and engineering fields.

This method is particularly useful when analytical solutions are difficult to obtain or do not exist, making numerical methods like fsolve() essential for practical problem-solving.

Statistical Analysis with SciPy：Conducting a Two-Sample t-test to Compare Means

September 22, 2024

Statistical Analysis with SciPy: Conducting a Two-Sample t-test to Compare Means

Here’s an example of a statistical analysis problem solved using $SciPy$.

We will perform a hypothesis test to determine if two independent samples come from populations with the same mean.

Problem: Two-Sample t-test

Scenario: You are a data analyst at a company that wants to compare the average sales between two different regions, Region A and Region B, over a given period.

You have collected sales data from each region.

Your goal is to determine if there is a statistically significant difference in average sales between the two regions using a two-sample t-test.

Hypothesis

Null Hypothesis (H₀): The means of the two populations (Region A and Region B) are equal.
Alternative Hypothesis (H₁): The means of the two populations are not equal.

Data

Let’s generate some sample data to simulate the sales figures from both regions:

Region A: $[23, 25, 21, 22, 20, 30, 24, 28, 19, 27]$
Region B: $[18, 20, 22, 24, 26, 19, 17, 21, 25, 23]$

Step-by-Step Solution Using SciPy

Import Required Libraries: We need $SciPy$ for statistical testing and $NumPy$ for handling numerical operations.
Perform the Two-Sample t-test: We will use $SciPy$’s ttest_ind() function to perform the test. This function compares the means of two independent samples.
Interpret the Results: We will interpret the p-value to decide whether to reject the null hypothesis.

Here is the code implementation:

import numpy as np
from scipy import stats

# Sample data for Region A and Region B
region_a = [23, 25, 21, 22, 20, 30, 24, 28, 19, 27]
region_b = [18, 20, 22, 24, 26, 19, 17, 21, 25, 23]

# Perform a two-sample t-test
t_stat, p_value = stats.ttest_ind(region_a, region_b)

# Print the results
print(f"T-statistic: {t_stat:.4f}")
print(f"P-value: {p_value:.4f}")

# Interpret the p-value
alpha = 0.05  # significance level
if p_value < alpha:
    print("Reject the null hypothesis: There is a significant difference between the means.")
else:
    print("Fail to reject the null hypothesis: No significant difference between the means.")

Explanation of the Output

T-statistic:
The t-statistic measures the difference between the group means relative to the variability in the samples.
A higher absolute t-value indicates a greater difference between the group means.
P-value:
The p-value tells us the probability of observing the data, or something more extreme, if the null hypothesis is true.
A low p-value (typically less than $0.05$) indicates that the observed difference is unlikely under the null hypothesis.
Decision:
- If the p-value is less than the significance level (α = $0.05$), we reject the null hypothesis, suggesting a significant difference between the two regions’ average sales.
- If the p-value is greater than $0.05$, we fail to reject the null hypothesis, implying no statistically significant difference.

Output

1
2
3

T-statistic: 1.6124
P-value: 0.1243
Fail to reject the null hypothesis: No significant difference between the means.

Explanation of the Results

T-statistic: 1.6124
The t-statistic measures the difference between the means of the two samples (Region A and Region B) relative to the variability in the data.
A t-statistic of $1.6124$ suggests there is some difference between the means, but it is not large enough on its own to be conclusive.
P-value: 0.1243
The p-value indicates the probability of observing the data, or something more extreme, if the null hypothesis (that the means are equal) is true.
In this case, the p-value is $0.1243$, which is greater than the typical significance level of $0.05$.
Conclusion: Fail to reject the null hypothesis
Since the p-value is greater than $0.05$, we do not have enough evidence to reject the null hypothesis.
This means that the observed difference in average sales between Region A and Region B is not statistically significant.
In simpler terms, there is no strong evidence to conclude that the means of the two regions are different.

Conclusion

$SciPy$’s ttest_ind() function makes it easy to perform hypothesis testing, allowing you to quickly assess whether differences in sample means are statistically significant.

This type of analysis is fundamental in comparing groups in various fields, including marketing, clinical trials, and product testing.