Electronic Band Structure in a 1D Crystal

Example Problem

In solid-state physics, one of the fundamental concepts is the electronic band structure.

A simple way to model this is using the tight-binding approximation for a 1D crystal with a single atomic orbital per site.

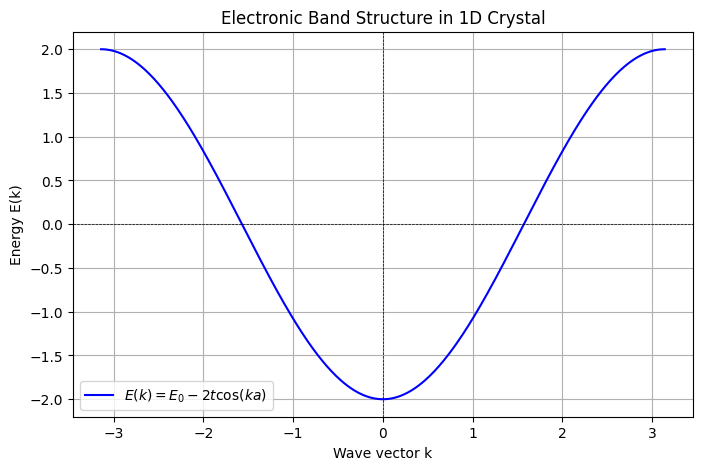
The energy dispersion relation for a one-dimensional crystal with lattice constant $ a $ and hopping energy $ t $ is given by:

$$
E(k) = E_0 - 2t \cos(ka)
$$

  • $ E(k) $ is the energy of the electron,
  • $ E_0 $ is the on-site energy,
  • $ t $ is the hopping integral,
  • $ k $ is the wave vector, and
  • $ a $ is the lattice constant.

This function represents a simple tight-binding model for a one-dimensional solid.

Python Implementation

Let’s compute and visualize the electronic band structure using $Python$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt

# Define parameters
a = 1.0    # Lattice constant
E0 = 0.0   # On-site energy
t = 1.0    # Hopping integral

# Define k values in the first Brillouin zone
k = np.linspace(-np.pi/a, np.pi/a, 500)

# Compute energy band structure
E_k = E0 - 2 * t * np.cos(k * a)

# Plot the band structure
plt.figure(figsize=(8, 5))
plt.plot(k, E_k, label="$E(k) = E_0 - 2t \cos(ka)$", color='b')
plt.axhline(0, color='black', linewidth=0.5, linestyle='--')
plt.axvline(0, color='black', linewidth=0.5, linestyle='--')
plt.xlabel("Wave vector k")
plt.ylabel("Energy E(k)")
plt.title("Electronic Band Structure in 1D Crystal")
plt.legend()
plt.grid()
plt.show()

Explanation

  1. We define the lattice constant $( a )$, on-site energy $( E_0 )$, and hopping integral $( t )$.
  2. We generate wave vectors $ k $ within the first Brillouin zone $ -\pi/a \leq k \leq \pi/a $.
  3. We compute the energy dispersion using $ E(k) = E_0 - 2t \cos(ka) $.
  4. We plot $ E(k) $ as a function of $ k $, showing the band structure of the 1D crystal.

Interpretation

  • The energy band has a cosine shape, typical for tight-binding models.
  • The bandwidth (difference between maximum and minimum $ E(k) $ ) is $ 4t $.
  • The band is symmetric around $ k = 0 $ due to the periodic nature of the lattice.

This is a basic yet powerful model for understanding electronic band structures in solids.