Optimal Taxation and the Laffer Curve

Problem Statement: Optimal Taxation and the Laffer Curve

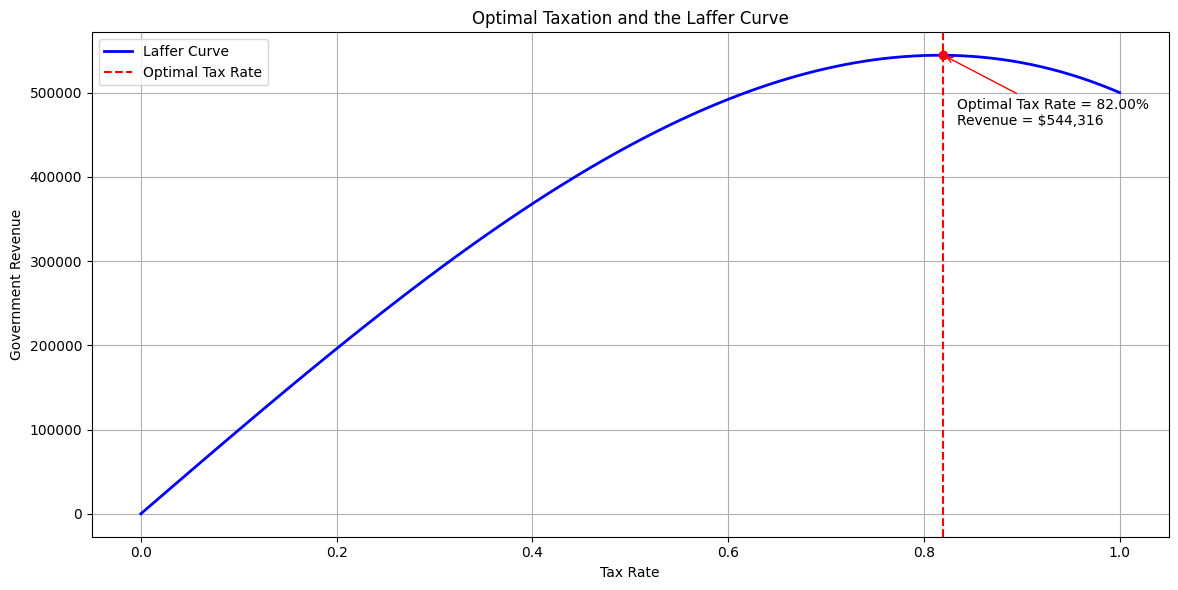
The Laffer Curve illustrates the relationship between tax rates and government revenue.

At very low tax rates, government revenue is minimal, and at very high tax rates, revenue also decreases because of reduced economic activity.

The goal is to:

  1. Simulate the Laffer Curve based on a theoretical economy.
  2. Identify the optimal tax rate that maximizes government revenue.
  3. Visualize the results.

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import numpy as np
import matplotlib.pyplot as plt

# Define the economy model
def government_revenue(tax_rate, max_income=1_000_000):
    """
    Simulates government revenue based on a tax rate.
    Revenue decreases at very high tax rates due to reduced economic activity.
    """
    # Economic activity decreases as tax rate increases
    economic_activity = max_income * (1 - 0.5 * tax_rate**2)
    revenue = tax_rate * economic_activity
    return max(0, revenue)  # Ensure revenue is non-negative

# Generate tax rates
tax_rates = np.linspace(0, 1, 101)  # Tax rates from 0% to 100%

# Compute government revenues for each tax rate
revenues = [government_revenue(rate) for rate in tax_rates]

# Find the optimal tax rate
optimal_index = np.argmax(revenues)
optimal_tax_rate = tax_rates[optimal_index]
optimal_revenue = revenues[optimal_index]

# Visualization
plt.figure(figsize=(12, 6))

# Laffer curve
plt.plot(tax_rates, revenues, label="Laffer Curve", color="blue", linewidth=2)
plt.axvline(optimal_tax_rate, color="red", linestyle="--", label="Optimal Tax Rate")
plt.scatter(optimal_tax_rate, optimal_revenue, color="red", zorder=5)
plt.title("Optimal Taxation and the Laffer Curve")
plt.xlabel("Tax Rate")
plt.ylabel("Government Revenue")
plt.legend()
plt.grid()

# Annotate the optimal point
plt.annotate(
    f"Optimal Tax Rate = {optimal_tax_rate:.2%}\nRevenue = ${optimal_revenue:,.0f}",
    (optimal_tax_rate, optimal_revenue),
    textcoords="offset points",
    xytext=(10, -50),
    arrowprops=dict(arrowstyle="->", color="red")
)

plt.tight_layout()
plt.show()

Explanation of the Code

  1. Economic Model:
    • The government_revenue function calculates revenue as $( \text{Revenue} = \text{Tax Rate} \times \text{Economic Activity} )$.
    • Economic activity decreases quadratically with higher tax rates, representing reduced incentives for productivity at high taxation levels.
  2. Simulation:
    • Tax rates range from $0$% to $100$%.
    • Government revenue is computed for each tax rate.
  3. Optimization:
    • The optimal tax rate corresponds to the maximum government revenue, determined using np.argmax.
  4. Visualization:
    • The Laffer Curve shows the relationship between tax rates and revenue.
    • The optimal tax rate is highlighted with a vertical line and annotated.

Results

  1. Laffer Curve:
    • The curve rises as the tax rate increases initially but falls after a certain point due to reduced economic activity.
  2. Optimal Tax Rate:
    • This is the tax rate where government revenue is maximized.
    • The plot includes a clear marker and annotation for this point.